keskeisen vaiheen 2 osasto muodostaa viimeisen osan ”neljästä operaatiosta” – neljä keskeistä matemaattista käsitettä, jotka oppilaiden tulee tuntea. Tämä blogi auttaa sinua varmistamaan, että kaikki oppilaat, vuodesta 3 vuoteen 6, voivat lähestyä jako luottamusta he tarvitsevat onnistua.
KS2 matematiikan jako perustuu siihen, mitä KS1: ssä on opittu. Loppuun mennessä Y2 opiskelijat odotetun standardin pystyy ’ muistaa ja käyttää kerto-ja jako tosiasiat 2, 5 ja 10 kertotaulut, mukaan lukien tunnistaa pariton ja parillinen numerot.”
vuoden 3 opettajille on aina hyvä varmistaa, että oppilaat tuntevat nämä erittäin hyvin. Tällä en tarkoita vain sitä, että he voivat toistaa jakautumisen tosiasioita teille, vaan he todella ymmärtävät, miten nämä tosiasiat esitetään sekä konkreettisin esityksin, sanallisin selityksin että muilla kuvallisilla menetelmillä.
opiskelijat, jotka eivät pysty tähän, mutta pystyvät kuitenkin kertomaan suullisesti jakautumisen faktat, heillä on hyvin pinnallinen käsitys jakamisesta ja jotta he voisivat edetä vaikeampiin ongelmanratkaisutoimiin, heidän käsitteellisen ymmärryksensä jakamisesta syventäminen on välttämätöntä 3.Vuonna.
valtakunnallisessa opetussuunnitelmassa jakolasku sijoittuu vuosille 3-5 kertolaskun kanssa samaan osioon ja se sijoitetaan vuonna 6 ”neljä operaatiota” – nimiseen osioon. Kansallisesta opetussuunnitelmasta otetut osat koskevat vain niitä, joissa erikseen mainitaan jako. Näiden osioiden muut elementit löytyvät tarvittaessa kerto-tai yhteen-ja vähennyslaskua käsittelevästä blogista.
Mikä On Jaos?
jakolasku on yksi neljästä operaatiosta – neljä keskeistä matemaattista käsitettä, jotka oppilaiden tulee tietää – yhteen-ja vähennyslaskun sekä kertolaskun ohella.
jos kertolasku yhdistää yhden luvun moneen kertaan, jakolasku on päinvastainen: lasketaan kuinka monta kertaa yksi luku sisältyy toiseen. Esimerkiksi jakamalla 10 luvulla 2 kysytään, kuinka monta kertaa 2 sisältyy 10: een.

.
Opetusjako KS2-teoria
jako on kertolaskun käänteisluku. Kuten kertolaskublogissa, myös jako – opetuksessa on kolme perusrakennetta, jotka yhdistettynä jakotietoihin ja käsitteelliseen ymmärtämiseen antavat oppilaille parhaan mahdollisuuden menestyä jaon ongelmiin liittyvissä ratkaisuissa.
kolme rakennetta ovat jakaminen, ryhmittely ja skaalaus. Vaikka ei ole tarpeeksi aikaa tutkia niitä perusteellisesti, mitä seuraa on vain lyhyt johdanto niihin.
jakaminen ja ryhmittely ovat kertolaskun käänteisluku toistuvana yhteenlaskuna. Jakaminen on KS1: ssä ja sitä aiemmin käyttöön otettu rakenteellinen käsite, jossa nimensä mukaisesti summa jaetaan tasa-arvoisiin ryhmiin.
esimerkiksi 12 omenaa jaetaan 3 oppilaan kesken. Kuinka monta omenaa kukin oppilas saa? Tässä tiedämme koko summan (12 omenaa) ja mikä tärkeintä, tiedämme, kuinka paljon aiomme jakaa (3). Riippuen siitä, missä opiskelijat ovat heidän matemaattinen matka, he voivat toistuvasti vähentää jonkin määrän (1, 2, 3 tai 4) määrästä kolmeen paalut, jotka edustavat kolme opiskelijaa.
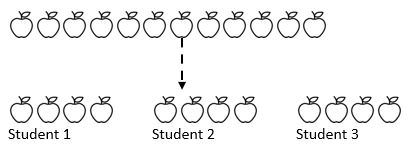
kuten edellä olevasta käy ilmi, koko summa on jaettu kolmeen yhtä suureen ryhmään.
ryhmittely on samanlainen kuin jakaminen, mutta se mitä tiedämme on hieman erilaista verrattuna jakamiseen. Jakamisrakenteessa tiedetään, kuinka paljon ryhmiä jaetaan. Ryhmittelyrakenteessa tiedetään kunkin ryhmän määrä, mutta ei varsinaisten ryhmien määrää.
esimerkiksi 12 omenaa jaetaan ryhmiin 4. Kuinka monta ryhmää tulee olemaan? Vaikka tämä kysymys on hyvin samankaltainen kuin edellä esitetty, se liittyy nyt ryhmittelyrakenteeseen, koska tiedämme, kuinka monta ryhmää kuhunkin ryhmään tulee, mutta emme enää tiedä, kuinka monta ryhmää nyt on.
koska tiedämme, että kussakin ryhmässä on 4 omenaa, voimme ryhmitellä 4 omenaa, kunnes olemme kattaneet kaikki 12, jotta näemme, että ryhmiä on 3.
jaon lopullinen rakenne on skaalaus. Vaikka kertolaskussa skaalasimme arvoa ylöspäin, jakorakenne skaalautuu alaspäin. Esimerkiksi Shannenilla on 6 kynää ja jenillä 3 kertaa vähemmän. Montako kynää jenillä on?
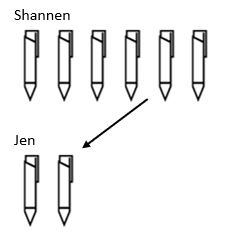
tässä voimme nähdä, että löytää kokonaismäärä kyniä, että Jen on, meidän piti ottaa määrä, että Shannen oli ja vähentää sitä asteikolla 3 niin, että Jen päätyy 2 kyniä.
kokemuksesta, tämä on vaikein jakorakenne opiskelijoiden ymmärtää ja ymmärtää ja on yksi, joka on tarkistettava yhdessä skaalaus kertolasku, koska tämä on ratkaiseva taito muunnettaessa mittauksia ja valuuttoja suuremmasta määrästä pienempään määrään. Esim. kilometreistä kilometreihin.
Jakovuosi 3
Englannin kansallisessa matematiikan opetussuunnitelmassa jokaiselle esitetylle matematiikan osa-alueelle on sekä lakisääteinen että ei-lakisääteinen Elementti. Lakisääteinen osa on seuraava:
- muistaa ja käyttää kerto-ja jakolaskutietoja 3, 4 ja 8 kertotaululle
- kirjoittaa ja laskea matemaattisia lausumia kerto-ja jakolaskulle käyttäen osaamiaan kertotauluja, myös kaksinumeroisille luvuille kertaa yksinumeroisille luvuille, käyttäen mentaalisia ja formaaleihin kirjallisiin menetelmiin edenneitä
- ratkovat ongelmia, mukaan lukien puuttuvat lukuongelmat, joihin liittyy kerto-ja jakolasku, mukaan lukien positiivisten kokonaislukujen skaalausongelmat ja kirjeenvaihtoon liittyvät ongelmat, joissa n-oliot ovat yhteydessä m-olioihin.
muut kuin lakisääteiset huomautukset ja ohjeet:
- oppilaat kehittävät tehokkaita mentaalisia menetelmiä esimerkiksi käyttämällä kommutatiivisuutta ja assosiatiivisuutta (esim., 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) ja kerto-ja jakolasku tosiasiat (esimerkiksi käyttämällä 3 × 2 = 6, 6 ÷ 3 = 2 ja 2 = 6 œ3) johtaa liittyvät tosiasiat (esimerkiksi, 30 × 2 = 60, 60 ÷ 3 = 20 ja 20 = 60 χ 3).
- oppilaat kehittävät luotettavia kirjallisia kertomis-ja jakomenetelmiä alkaen kaksinumeroisten lukujen laskemisesta yksinumeroisilla luvuilla ja edeten lyhyiden kerto-ja jakolaskujen muodollisiin kirjallisiin menetelmiin.
- oppilaat ratkaisevat asiayhteyksissä yksinkertaisia ongelmia ja päättävät, mitä neljästä operaatiosta käytetään ja miksi. Näitä ovat esimerkiksi mittaus-ja skaalauskontekstit (esimerkiksi neljä kertaa niin korkea, kahdeksan kertaa niin pitkä jne.) ja kirjeenvaihtoon liittyviä ongelmia, joissa m-esineet ovat yhteydessä n-esineisiin (esimerkiksi 3 hattua ja 4 takkia, kuinka monta eri asua?; 12 makeista jaettiin tasan 4 lapsen kesken, 4 kakkua tasan 8 lapsen kesken).
Jaostotoiminta Vuosi 3
tämä ei kata opetusta sinänsä, mutta antaa oppaan siitä, miten jakoa voidaan opettaa käsitteellisesti tässä vaiheessa. Edellytyksenä tälle olisi siihen liittyvien kertolaskujen opettaminen ensin ennen minkään siihen liittyvän jaon opettamista.
rakenteita mietittäessä on parasta, että tässä osassa opiskelijoiden oppimismatkaa pysytään ryhmittelyssä ja jakamisessa. Seuraavia esimerkkejä, tarkastelemme kehittää opiskelijoiden ymmärrystä jakamalla 4. Se noudattaa Konkreettis-kuvallis-abstraktia lähestymistapaa.
usein opiskelijoiden käsitys lukumäärästä voi rajoittaa heidän etenemistään jakolaskussa. Varsinkin kun kyse on ryhmittelystä ja jakamisesta, kun kokonaisuudesta otetaan jatkuvasti vain yksi pois.
opetusjaon alusta lähtien opettajien tulisi tukeutua siihen, mitä oppilaat jo tietävät parillisista luvuista ja muista numerotiedoista edistääkseen oppilaita laskemaan missä tahansa sopivassa numerossa.
laskureita voidaan käyttää osoittamaan toisiinsa liittyviä jakotietoja, sillä opiskelijat ovat käyttäneet opinnäytetöitä rakentaessaan käsitteellistä käsitystään kertolaskusta. Esimerkiksi: ’kuinka monta ryhmää 4 on olemassa?”ja” kuinka monta on kussakin ryhmässä?”olisi kysyttävä ja vastausten olisi liityttävä siihen, miten tämä osoittaa kahtiajakoa.
Opettaja:montako laskuria on?
Lapsi: Neljä
Opettaja: Hyvä. Tämä on neljän hengen ryhmä. Kuinka monta neljän hengen ryhmää on olemassa?
Lapsi: Yksi
Opettaja: Erinomainen. Meillä on neljä laskijaa yhdessä ryhmässä. Olemme ryhmitelleet neljä laskijaa yhteen ryhmään. Mitä olemme tehneet?
lapsi: ryhmitelty neljä laskijaa yhdeksi ryhmäksi.
Opettaja: Loistava. Kun ryhmitämme neljä laskuria yhdeksi ryhmäksi, olemme tehneet matemaattisen laskennan neljästä jaettuna yhdellä. Mitä laskelmia teimme?
lapsi: neljä jaettuna yhdellä.
opettaja: ja kun ratkaisemme neljä jaettuna yhdellä, vastaus on neljä, koska olemme tehneet yhden ryhmän, jossa on neljä kohdetta. Neljä jaettuna yhdellä on neljä. Mikä on neljä jaettuna yhdellä?
lapsi: Neljä jaettuna yhdellä on neljä.
Opettaja: erinomainen
voit nähdä, miten se toistuisi seuraaville:
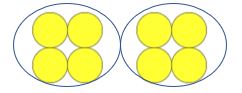
Opettaja:montako laskuria on?
lapsi: kahdeksan
Opettaja: Hyvä, Tämä on neljän hengen ryhmä. Kuinka monta neljän hengen ryhmää on olemassa?
Lapsi: Kaksi
Opettaja: Erinomainen. Meillä on neljä laskijaa yhdessä ryhmässä. Olemme ryhmitelleet neljä laskijaa kahteen ryhmään. Mitä olemme tehneet?
lapsi: ryhmitelty neljä laskijaa kahteen ryhmään.
Opettaja: Loistava. Kun ryhmitämme neljä laskijaa kahteen ryhmään, olemme tehneet matemaattisen laskennan kahdeksasta jaettuna kahdella. Mitä laskelmia teimme?
lapsi: kahdeksan jaettuna kahdella.
opettaja: ja kun ratkaisemme kahdeksan jaettuna kahdella, vastaus on neljä, koska olemme tehneet kaksi ryhmää, joissa on neljä kohdetta. Kahdeksan jaettuna kahdella on neljä. Mikä on kahdeksan jaettuna kahdella?
lapsi: kahdeksan jaettuna kahdella on neljä.
Opettaja: erinomainen
kun opiskelijat alkavat olla luottavaisia tämän kanssa, voimme siirtyä muihin malleihin, kuten Cuisenaire-sauvoihin.

tässä koko määrä on edustettuna alkuun juna ja violetti sauva (joka tässä tapauksessa edustaa 4 ja jos olet lukenut muita blogeja tässä sarjassa toivottavasti tiedät, kuinka paljon puolestapuhuja olen niiden käyttöä luokkahuoneessa ja niin opiskelijat ovat tietoisia sen arvosta silloin) käytetään osoittamaan, kuinka monta ryhmää 4 voi mennä kokonaismäärä.
oppilaat voivat sitten siirtyä piirtämään opettajan lukemia skenaarioita. Esimerkiksi. Painikkeita on 24 ja ne on ryhmiteltävä 4. Montako ryhmää on? Opiskelijat voisivat piirtää nuo painikkeet ja ryhmitellä ne 4 jne.
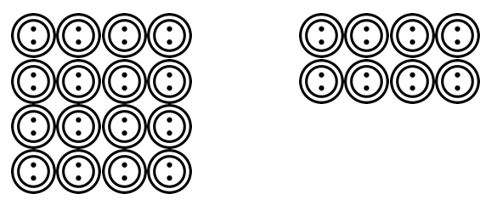
kun opiskelijat ovat tottuneet siihen, että he pystyvät visualisoimaan nämä ryhmittelyt tai jakoskenaariot erilaisissa yhteyksissä, he voivat siirtyä abstraktimpiin edustustoihin matemaattisten symbolien avulla.

3 Long Division-laskentataulukot vuosille 3-6
Hanki oppilaasi valmistautumaan Long Divisioniin koko KS2: ssa näillä pitkäjakoisilla laskentataulukoilla.
divisioonan Sanaongelmat Vuosi 3
Sanaongelmat vuonna 3 käyttävät yleisesti ryhmittely-tai jakamisrakennetta.
leivoksia on 40 ja oppilaita 10. Montako kakkua kukin oppilas saisi?
koska tiedämme, kuinka monta ryhmää on (10), meidän täytyy selvittää määrä ryhmää kohti, joten tämä on jakamisrakenne. Opiskelijoiden odotetaan käyttävän tietämystään 4 kertaa taulukon selvittää tämän ja saada vastaus 4.
alue: Päättely ja ongelmanratkaisu Vuosi 3
päättelyyn ja ongelmanratkaisuun hyvä toiminta mielestäni on sanaongelman sovittaminen laskutoimitukseen. Esimerkiksi:
Match sana ongelmia, jotka ratkaistaan tietämällä 20 jaettuna 4.
- kyniä on 20 ja ne sijoitetaan 5 kappaleen pakkauksiin. Montako kussakin pakkauksessa on?
- lyijykyniä oli 20 ja sitten opiskelija tuo 4 Lisää. Montako kynää on nyt?
- kyniä on 20 ja ne sijoitetaan 4 kappaleen pakkauksiin. Montako kussakin pakkauksessa on?
- kyniä oli 20 ja sitten katosi 4. Montako kynää on nyt?
oppilaiden saaminen kirjoittamaan selityksensä jokaiseen kysymykseen on hyödyllistä, koska se mahdollistaa heidän ajattelunsa näkemisen. Kysymykset on valittu huolellisesti niin, että jokaisen kysymyksen numerot liittyvät kysymyksessä oleviin numeroihin, joten opiskelijat luottavat matemaattisiin taitoihinsa päättelemään oikean vastauksen.
Jakovuosi 4
Englannin kansallisessa matematiikan opetussuunnitelmassa jokaiselle esitetylle matematiikan osa-alueelle on sekä lakisääteinen että ei-lakisääteinen Elementti. Lakisääteinen osa on seuraava:
- kerto – ja jakolaskutietoja muistutetaan kertotaulukoissa, joiden arvo on enintään 12 × 12
- käytä paikan arvoa, tunnettuja ja johdettuja faktoja kertoaksesi ja jakaaksesi henkisesti, mukaan lukien: kertomalla 0: lla ja 1: llä; jakamalla 1: llä; kertomalla yhteen kolme lukua
Ei-lakisääteiset huomautukset ja ohjeet:
- oppilaat harjoittelevat edelleen kertotaulujen ja niihin liittyvien jakotietojen muistamista ja käyttöä sujuvuuden edistämiseksi.
- oppilaat harjoittelevat henkisiä menetelmiä ja laajentavat tämän kolminumeroisiin lukuihin tosiasioiden johtamiseksi (esimerkiksi 600 œ3 = 200 voidaan johtaa 2 x 3 = 6).
- oppilaat harjoittelevat tullakseen sujuviksi muodollisen kirjallisen lyhyen kertolaskun ja lyhyen jakolaskun menetelmässä tarkkojen vastausten avulla
- oppilaat ratkovat kaksivaiheisia ongelmia yhteyksissä, valitsevat sopivan leikkauksen ja työskentelevät yhä vaikeammilla luvuilla. Tähän tulisi sisältyä kirjeenvaihtokysymyksiä, kuten ruokalistalla olevan aterian valintojen määrä tai kolme kakkua, jotka on jaettu tasan 10 lapsen kesken.
Jakotuntiideat vuosi 4
tätä oppituntia varten katson, miten voit alkaa opettaa lyhytjakoa käyttäen manipulatiiveja sen rinnalla.
sano, että aiomme opettaa opiskelijoille lyhytjaon kysymykseen 168 jaettuna 12: lla.
normaalisti kirjoittaisimme tämän niin sanottuun bussipysäkkiin. Mielenkiintoista on kuitenkin se, että eri puolilla maailmaa kirjoitetaan eri tavalla.
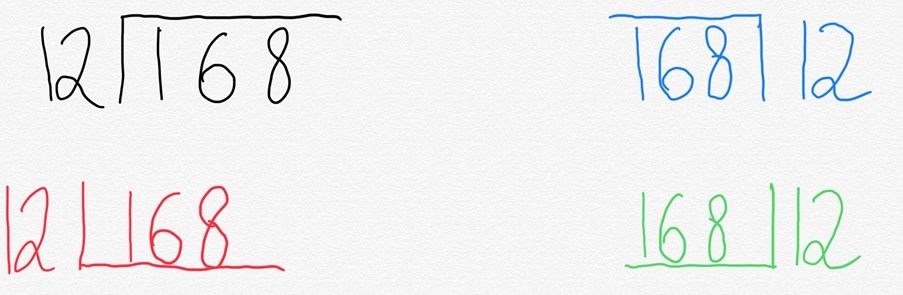
syy tähän on melko yksinkertainen. Se, mitä ”bussipysäkki” todellisuudessa edustaa, on lyhennetty tapa edustaa suorakulmiota.
kun opetamme muodollista lyhytjakoa, käytännössä sanomme, että on kuviteltava suorakulmio, jonka leveys on 12. Suorakulmion kokonaispinta-ala on 168 ja yritämme löytää puuttuvan pituuden ylhäältä. Miten näytämme tämän manipulatiiveilla? Dieenilohkot ovat tässä hyödyllinen työkalu.
tiedämme yhteismäärän olevan 168. Joten meidän täytyy kerätä 168 arvoinen dienes käyttäen pienimpiä määriä lohkojen mahdollista. Tämä on esitetty alla.
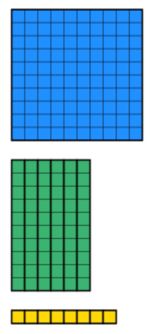
kun asiaa katsoo taaksepäin, tiedämme, että leveys on 12. Se tarkoittaa, että nyt pitää manipuloida palikoita niin, että saadaan leveyttä 12. Huomaa, että suorakulmion, on oltava vankka ja voi olla puuttuvia osia. Esimerkiksi alla olevaa ei sallittaisi, vaikka leveyttä alaspäin meneviä yksiköitä olisi 12 kappaletta.
sen sijaan opiskelijat voivat kiertää kaksi 10: n korttelia saadakseen seuraavat. Huomaa, miten kussakin sarakkeessa on 12 ja se on kiinteä esine.
viimeinen osa, joka opiskelijoiden on tehtävä, on käyttää jäljellä olevia lohkoja luodakseen myydyn suorakulmion pitäen samalla leveyden 12. Tämä voi kestää jonkin aikaa, mutta käytännössä opiskelijat saavat nopeammin. Jonkin ajan kuluttua opiskelijat tuottavat tämän:
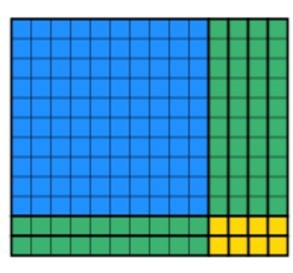
voimme nähdä, että kaikki 168 korttelin arvo on käytetty loppuun ja leveys on edelleen 12. Vastauksen löytämiseksi opiskelijoiden on laskettava pituus, joka tässä tapauksessa on 14. Olen päällekkäin molemmat menetelmät alla, joten voit nähdä, miten ne täydentävät toisiaan alla.
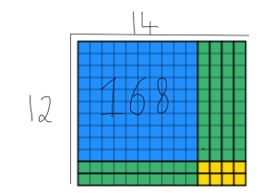
tämä on hyödyllinen strategia opettaa opiskelijoille vuonna 4, koska on massiivisia vaikutuksia muilla aloilla opetussuunnitelman, jotka on jo valaistu opiskelijoille.
vaikka he eivät ehkä vielä tunnista sitä, opettamalla tällaista lyhyttä jakoa he ovat jo tutustuneet ympärys – ja pinta-alaan-ajatelkaa, kuinka paljon opetusaikaa voidaan säästää, kun tämä yhteys tehdään. Ei vain sitä, mutta toissijaisesti tämä lähestymistapa siirtyy algebralliseen ajatteluun.
Jakosanaongelmat vuosi 4
opiskelijoiden odotettaisiin hyödyntävän tietoaan paikan arvosta jakoperusteisten ongelmien ratkaisemiseksi, joten sopiva sanaongelma olisi.
tarhassa kasvatettiin 4 800 omenaa kaudessa. Ne asetetaan 4 kappaleen pakkauksissa ennen markkinoille menoa. Montako askia on?
tässä opiskelijan tulee käyttää sitä, että 4 x 12 = 48 Ja koska 4 800 on sata kertaa enemmän kuin 48, 12 on myös kerrottava 100: lla, jotta saadaan 1 200
jako: Päättely ja ongelmanratkaisu vuosi 4
onko aina, joskus tai ei koskaan totta, että kolmen parillisen luvun summa on jaollinen 4: llä?
tämä kysymys antaa opiskelijoille runsaasti mahdollisuuksia kokeilla kysymyksen parametrien puitteissa. Enemmän tukea tarvitsevat opiskelijat voivat katsoa sing digit-parillisia numeroita ja oppilaat voivat mennä mihin tahansa, mikä heille sopii.
tämänkaltaisissa avoimissa kysymyksissä on hyvä asettaa vähimmäisvaatimus sille, kuinka monta yritystä opiskelijoiden tulisi tehdä, muuten he usein päättävät tehdä minimin.
vastaus tähän kysymykseen on joskus.
nopea ”temppu” tietää, onko luku jaollinen, on katsoa luvun 2 viimeistä numeroa ja katsoa, ovatko ne jaollisia 4: llä. Esimerkiksi, jos lapsi löytyi summa 34, 36 ja 38 ja sai 108, kuten opettaja tiedän, että tämä numero on jaollinen 4 kuin kaksi viimeistä numeroa (08) tehdä 8 ja on jaollinen 4. Jos lapsi valitsi 34, 36 ja 48 saada 118, tiedän, että tämä ei ole jaollinen 4 kuin 18 – kaksi viimeistä numeroa 118 – ei ole jaollinen 4.
Jakovuosi 5
Englannin kansallisessa matematiikan opetussuunnitelmassa jokaiselle esitetylle matematiikan osa-alueelle on sekä lakisääteinen että ei-lakisääteinen Elementti. Lakisääteinen osa on seuraava:
- kerro ja jaa numerot henkisesti käyttäen tunnettuja faktoja
- Jaa luvut 4-numeroisiin numeroihin yksinumeroisella luvulla käyttäen muodollista kirjallista lyhytjaon menetelmää ja tulkitse jäännökset asiayhteyden kannalta tarkoituksenmukaisesti
- kerro Ja Jaa kokonaisluvut ja desimaaleja sisältävät luvut 10, 100 ja 1000
- ratkaisevat kerto-ja jakolaskuun liittyvät ongelmat, mukaan lukien niiden tekijöiden tuntemus ja kerrannaiset, neliöt ja kuutiot
- ratkaisevat yhteen -, vähennys -, kerto-ja jakolaskuongelmat sekä nämä, mukaan lukien yhtäsuuruusmerkin
- merkityksen ymmärtäminen, ratkaisevat kerto-ja jakolaskuun liittyviä ongelmia, mukaan lukien yksinkertaisilla murtoluvuilla tapahtuva skaalaus ja yksinkertaisiin korkoihin liittyvät ongelmat.
muut kuin lakisääteiset huomautukset ja ohjeet:
- oppilaat tulkitsevat ei-kokonaislukuvastauksia jakolaskuun ilmaisemalla tulokset eri tavoin asiayhteyden mukaan, myös jäännöksillä, murtolukuina, desimaaleina tai pyöristämällä (esimerkiksi 98 χ 4 = = 24 r 2 = 24 = 24, 5 ≈ 25).
- oppilaat käyttävät kerto-ja jakolaskua käänteislukuina tukemaan suhdeluvun käyttöönottoa vuonna 6, esimerkiksi kertomalla ja jakamalla potenssilla 10 mittakaavoissa tai kertomalla ja jakamalla potenssilla 1000 muunnettaessa yksiköiden, kuten kilometrien ja metrien välillä.
jakotoiminnot Vuosi 5
Jakovuosi 5 etenee siten, että vastauksissa käytetään jäännöksiä. Tämän oppitunnin, aion tarkastella toista käyttöä manipulatiivit että opettajat voivat käyttää opettaa 4-by-1-numeroinen jako.
jos kysymys oli 5 642 jaettuna 4: llä, voisimme esittää tämän käyttämällä paikkakaaviota ja paikkalaskureita, kuten alla näkyy.
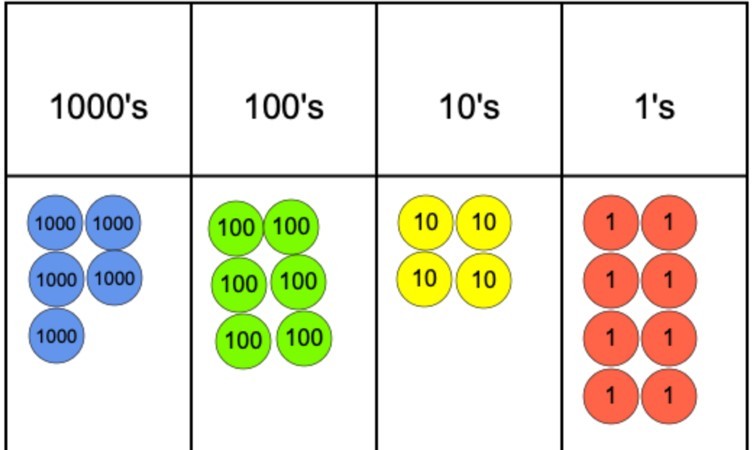
seuraava askel olisi alkaa ryhmitellä laskurit osaksi 4 koska tämä on meidän jakaja. Kuitenkin, kuten voidaan nähdä, tulemme nopeasti ongelma 1000: n sarakkeessa, koska voimme ryhmä 4 laskurit, mutta sitten emme voi ryhmitellä jäljellä laskuri ryhmässä 4.
tämän ongelman torjumiseksi ryhmittelemättä jäänyt 1000 laskuri voidaan vaihtaa kymmeneen 100 laskuriin. Nämä voidaan sitten ryhmitellä ryhmiin 4 ja tämä voi tapahtua ilman, että 100s laskurit jäljellä. Sieltä se on yksinkertainen tapaus, että sitten siirrytään kymppiin ja lopulta ykkösiin.
koska 1s-laskijoita on yhdeksän, voimme ryhmitellä niistä 8 2-ja 4-ryhmiin ja väittää, että on yksi yli*. Vastauksen löytämiseksi kaikki, mitä tarvitaan, on laskea ryhmien määrä kussakin paikassa arvo ja käyttää näitä kirjoittaa numeroita luoda lopullinen vastaus. Tällöin vastaus olisi 1 412 jäljellä 1.
* desimaaleja tarkasteltaessa voidaan vaihtaa jäljellä oleva 1s-laskuri kymmeneen 0,1-laskuriin ja jatkaa jakoa edellä kuvatulla tavalla. Opiskelijat tuntevat tämän mallin on hyödyllistä, koska se voi auttaa demystify jako desimaaleja, jotka opiskelijat voivat kamppailla. Tämä auttaa heitä näkemään, että kyse on pikemminkin heille jo tutun prosessin jatkumisesta kuin jostain uudesta.
jako-ongelmat Vuosi 5
jakaessaan vuonna 5 opiskelijat törmäävät skenaarioihin, joissa heidän on pyöräytettävä vastauksensa, jotta vastaus olisi asiayhteydessä järkevä. Sopiva kysymys, joka osoittaa tämän, olisi suunnilleen seuraava:
koulu suunnittelee sosiaalista etäännytettyä diskoa, jossa he aikovat tarjota jokaiselle oppilaalle 250 ml mehua. He voivat ostaa 2 litran pulloja mehua. He odottavat 33 oppilasta saapuvaksi, joten tietäkää, että he antavat 8,25 litraa mehua. Kuinka monta pulloa mehua pitää ostaa?
yleinen vastaus on, että opiskelijat sanovat 4 ja neljäsosa. Kuitenkin, koska et voi ostaa neljäsosa pullon, tässä tapauksessa oikea vastaus olisi 5 pulloa mehua tarvittaisiin varmistaa, että kaikki opiskelijat voisivat osallistua.
jako: päättely ja ongelmanratkaisu Vuosi 5
kuten edellä todettiin, vuonna 5 opiskelijat kohtaavat divisioonassa skenaarioita, joissa heidän on valittava, onko vastaus pyöristettävä ylös-vai alaspäin. Esimerkiksi kun kysymyksessä oppilaita pyydetään selvittämään, kuinka monta bussia koulumatkaan tarvitaan.
oppilaiden saaminen luomaan omia ongelmiaan käyttämällä erilaisia tarjottuja asiayhteyksiä voi olla todella haastavaa toimintaa, joka saa opiskelijat ajattelemaan matemaattisesti asiayhteyttä ja jakoa.
opiskelijat voivat sitten vaihtaa nämä kehittämänsä kysymykset kumppanin kanssa ja lähteä sitten ratkomaan niitä ja kysymään alkuperäisen kysymyksen luojalta, onko heillä oikea vastaus.
Jakovuosi 6
Englannin kansallisessa matematiikan opetussuunnitelmassa jokaiselle esitetylle matematiikan osa-alueelle on sekä lakisääteinen että ei-lakisääteinen Elementti. Lakisääteinen osa on seuraava:
- Jaa enintään 4-numeroiset luvut kaksinumeroisella kokonaisluvulla käyttäen pitkän jakolaskun muodollista kirjallista menetelmää ja tulkitse jäännökset kokonaislukuina, murtolukuina tai pyöristämällä asiayhteyden mukaan
- Jaa enintään 4-numeroiset luvut kaksinumeroisella numerolla käyttäen muodollista kirjallista lyhyen jakolaskun menetelmää tarvittaessa tulkiten jäännökset asiayhteyden mukaan
- suorita mielellisiä laskelmia, myös sekaoperaatioilla ja suurella luvut
- tunnistavat yhteiset tekijät, yhteiset kerrannaiset ja alkuluvut
- käyttävät tietojaan operaatiojärjestyksestä tehdäkseen laskelmia, joissa on mukana neljä operaatiota
ei-lakisääteiset huomautukset ja ohjeet:
- ratkaise yhteen -, vähennys -, kerto-ja jako-ongelmia
- käytä estimointia laskutoimitusten vastausten tarkistamiseen ja ongelman yhteydessä sopivan tarkkuusasteen määrittämiseen.
Division Lesson Ideas Year 6
Sophie Bartlett (@_MissieBee) on luonut täällä erinomaisen blogin (linkki Sophien blogiin long Divisionin opettamisesta), jossa kerrotaan, miten hän opettaisi long Divisionia vuoden 6 luokalla. Koska pitkä jako on ainoa Uusi oppiminen jako Vuosi 6, Tämä on ihanteellinen tapa ottaa käyttöön menettely pitkä jako.
Jakokysymykset Vuosi 6
tyypillinen jakosanaongelma, johon vuoden 6 oppilas törmäisi, olisi:
koulu keräsi myyjäisistä 3 146 puntaa. Tilaisuuteen osallistui 104 vanhempaa. Jos kaikki vanhemmat käyttivät yhtä paljon rahaa, kuinka paljon kukin vanhempi käytti?
tässä opiskelijoiden odotettaisiin käyttävän long division-menetelmää tämän kysymyksen ratkaisemiseksi saadakseen vastauksen 30,25 puntaa.
jako: päättely ja ongelmanratkaisu Vuosi 6
jonkin prosessuaalisen kuten pitkän jakovaiheen avulla hyvä päättelytoiminta on saada oppilaat löytämään virheitä. Nämä varat tarjoavat suuren pankin tällaista toimintaa. Kuten voimme nähdä alla olevasta kysymyksestä, oppilaat ovat tehneet kaiken kovan työn, mutta huolimaton virhe laskettaessa ryhmiä 59 tarkoittaa, että lapsi uskoi 59 x 7 oli 472 eikä 59 x 8.
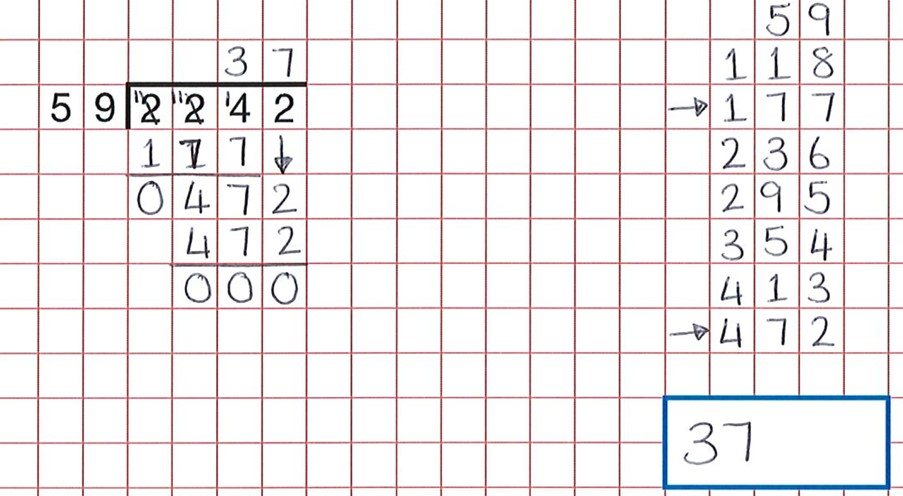
oikea vastaus olisi ollut 38.
jako on keskeinen matematiikan aihe, ei vain KS2: ssa vaan koko matematiikassa. Toivottavasti tämä viesti on antanut sinulle hyviä ideoita auttaa oppilaita lähestyä sitä luottavaisin mielin.
Online 1-to-1 matematiikan tunnit, joihin koulut ja opettajat luottavat
joka viikko Third Space Learningin matematiikan erikoisopettajat tukevat tuhansia alakoululaisia viikoittaisilla 1-to-1-tunneilla ja matematiikkainterventioilla. Vuodesta 2013 lähtien olemme auttaneet yli 100 000 lasta tulemaan itsevarmemmiksi, kykeneviksi matemaatikoiksi. Lisätietoja tai pyydä henkilökohtainen tarjous puhua meille tarpeistasi ja miten voimme auttaa.
peruskoulun opetus on suunnattu kunkin lapsen tarpeisiin ja noudattaa tarkasti kansallista opetussuunnitelmaa.