ebben az útmutatóban elmagyarázom, mi a standard hiba képlet, és hogyan kell használni a standard hiba kidolgozásához egy példa segítségével.
mi a standard hiba?
a standard hiba (SE), amelyet néha az átlag standard hibájának (SEM) neveznek, olyan statisztika, amely megfelel a mintavételi Eloszlás szórásának az átlagértékhez viszonyítva. De mi is ez valójában?
mondja, hogy érdekli az átlagéletkor az Egyesült Királyságban az Alzheimer-kórt diagnosztizálják. Ezt nem lehet mindenki számára meghatározni az Egyesült Királyságban, ezért a kutatók mintát vesznek a populációból, hogy általánosítsák az Általános számot. Például, 10.000 Brit ember a betegség lehet elemezni, és fogják használni, hogy létrehoz az átlagos életkor a diagnózis. Ha ezt 5000 betegből álló véletlenszerű mintán végzi, akkor a diagnózis átlagos életkora 61,5 év lehet. Ha azonban a mintaelemzést külön, 10 000 másik betegből álló véletlenszerű mintán végzi, akkor átlagosan 62,3 év lehet. Tegyük fel, természetesen hipotetikusan, hogy ha képesek lennének elemezni az Egyesült Királyságban az összes Alzheimer-kórban szenvedő embert, hogy megkapják a tényleges számot, akkor 64,3 évet kaphatnának. Látható, hogy a mintapopulációkból nyert adatok (61,5 és 62,3 év) eltérnek a tényleges adatoktól (64,3 év). Ez az átlagértékek változása várható, és ahogy növeli a mintapopulációban lévő emberek számát, olyan értéket kap, amely közelebb áll a tényleges értékhez. Pontosan ezt jelenti a standard hiba. A standard hiba a mintapopulációk közötti átlagértékek ezen változását jelzi.
további olvasmányként azt javaslom, hogy olvassa el Douglas Altman és Martin Bland professzorok rövid statisztikai feljegyzését, amelyet a British Medical Journal publikált. Ez egy hasznos betekintést, hogy mi a standard hiba, és mi a különbség a szórás.
a standard hiba képlete
a standard hiba kiszámításához két információra van szükség: a szórásra és az adatkészletben lévő minták számára. A standard hibát úgy számítjuk ki, hogy a szórást elosztjuk a minták számának négyzetgyökével.
itt található a teljes annotált standard hiba képlet:
példa
a standard hiba képletének jobb megértéséhez segíthet egy példa áttekintésében. Tegyük fel, hogy 80 emberünk van, és érdekel a magasságuk. Mérjük a magasságukat, és kiszámítjuk a szórást 30,6 cm-re. Most be kell illesztenünk ezeket az értékeket az egyenletünkbe:
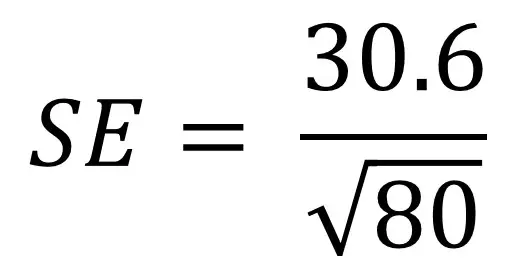ha kényelmetlenül érzi magát az egyenletek számológépekbe történő bevitelével, akkor a képletet kezelhető darabokra bonthatja. Itt vannak a lépések, amelyeket megtehet.
- először számítsuk ki a minták számának négyzetgyökét (n). Ebben az esetben n 80. A 80 négyzetgyöke 8,94.
- ezután ossza el a szórást (30,6) a 80 (8,94) négyzetgyökével. Ez 3,42 értéket ad.
- ezért a populációnkban a magasság standard hibája 3,42 cm.