a csúcsok, az arcok és az élek sokat jelennek meg az általános iskolai geometriában, amikor a gyerekek megismerik a 3D formák tulajdonságait. Itt elmagyarázzuk, hogy ezek mindegyike mit jelent, és hogyan lehet kiszámítani a csúcsok, arcok és élek számát bármilyen alakzathoz. A leggyakoribb alakzatok éleinek, arcainak és csúcsainak számát is tartalmazza.
ezt a szókincset a 2.évfolyamon vezetik be a nemzeti tantervbe, így a következő információkat az általános iskolai évek során a tanulók használhatják. Még az 1. év tanulói is elkezdhetnek ilyen módon foglalkozni a formák tulajdonságaival, ha előnyt akarsz adni nekik!
mik azok a csúcsok az alakzatokban?
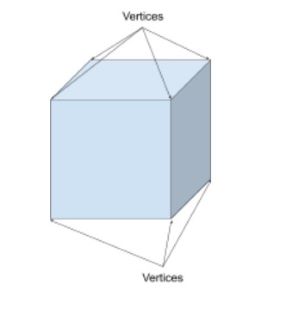
az alakzatok csúcsai azok a pontok, ahol két vagy több vonalszakasz vagy él találkozik (mint egy sarok). A csúcsok egyes száma csúcs. Például egy kockának 8 csúcsa van, a kúpnak pedig egy csúcsa.
a csúcsokat néha sarkoknak nevezik, de amikor 2D és 3D alakzatokkal foglalkozunk, a csúcsok szót részesítjük előnyben.
egy kockának 8 csúcsa van. 7 látható itt, egy pedig rejtett.
mik az élek?
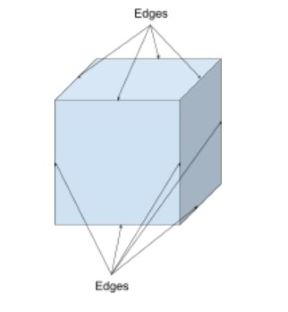
az élek azok a vonalszakaszok, amelyek az egyik csúcsot a másikhoz kötik, és ahol az alakzat arcai találkoznak. Ezeket 2D és 3D alakzatok leírására lehet használni.
bár sok alakzat egyenes vonalakkal és egyenes élekkel rendelkezik, vannak olyan alakzatok, amelyeknek ívelt élei vannak, például egy félgömb. Egy kockának 12 egyenes éle lesz az alábbiak szerint; 9 látható, 3 pedig rejtett.

ingyenes 3D alakzatok független összefoglaló munkalapok
segítsen a 2. év (és idősebb) tanulóinak a csúcsok, arcok és élek felülvizsgálatában az ingyenes független összefoglaló munkalapokkal.
mik azok az arcok?
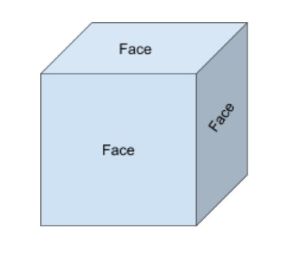
az arcok a szilárd forma sík felülete. Például egy kockának 6 arca van. Amikor a 2d és 3D alakzatokra gondolunk, fontos tudni, hogy a 2d alakzat csupán a 3d alakzat arcát képviseli.
azt is fontos tudni, hogy mivel valóságunk 3 dimenzióban épül fel, lehetetlen fizikailag kezelni a 2d alakzatokat, mivel 3 dimenziós alakzatok vesznek körül minket. Ezért, ha az osztályteremben van egy 2D alakzatok feliratú fiók, ezt el kell távolítani, mivel tévhitet tanít a gyerekeknek. Bár az osztályterem interaktív koncepciója, a 2d alakzatok csak 2 dimenziós rajzként létezhetnek.
lehet mind lapos, mind ívelt Arc, de hasznosnak tartom az ívelt arcokat ívelt felületeknek nevezni, mivel jól illeszkedik az alak látványához.
három arc látható, három pedig el van rejtve az alábbi kockán.
közös 3D alakzatok csúcsai, arcai és élei
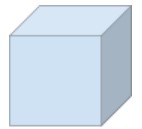
hány arca, éle és csúcsa van egy kockának?
egy kockának 8 csúcsa van.
egy négyszögnek 12 éle van.
egy kockának 6 arca van.

hány arca, éle és csúcsa van egy hengernek?
egy hengernek 0 csúcsa van.
egy hengernek 2 éle van.
egy hengernek 2 felülete és 1 ívelt felülete van.

hány arca, éle és csúcsa van egy félgömbnek?
egy félgömbnek 0 csúcsa van.
egy félgömb 1 ívelt éllel rendelkezik.
egy félgömb 1 arccal és 1 ívelt felülettel rendelkezik.

hány arca, éle és csúcsa van egy kúpnak?
egy kúpnak 1 csúcsa van.
a kúpnak 1 éle van.
egy félgömb 1 arccal és 1 ívelt felülettel rendelkezik.

hány arca, éle és csúcsa van egy tetraédernek?
egy tetraédernek 4 csúcsa van.
egy tetraédernek 6 éle van.
a tetraédernek 4 arca van.

hány arca, éle és csúcsa van egy gömbnek?
egy gömbnek 0 csúcsa van.
egy tetraédernek 0 éle van.
a tetraéder 1 ívelt felülettel rendelkezik.

hány arca, éle és csúcsa van egy prizmának?
a prizma szilárd tárgy, geometriai forma vagy poliéder, ahol mindkét vég felülete azonos alakú. Mint ilyen, a hallgatók sokféle prizmával találkoznak iskolájuk során. A közösek közé tartoznak a kockák, kockák, háromszög alakú prizmák, ötszögletű prizmák és hatszögletű prizmák.
| alak | képi | arcok | élek | csúcsok |
|---|---|---|---|---|
| háromszög alakú prizma | 5 | 9 | 6 | |
| ötszögletű prizma | 7 | 15 | 10 | |
| hatszögletű prizma | 8 | 18 | 12 | |
| Cube |
 |
6 | 8 | 12 |
| kocka alakú |  |
6 | 8 | 12 |
mikor tanulnak a gyerekek az általános iskolában a csúcsokról, az arcokról és az élekről?
a 2.évben a geometria tanulmányozása során a gyerekeket hivatalosan be kell vezetni a csúcsok, arcok és élek szókincsébe. A tanárok azonban dönthetnek úgy, hogy ezt a szókincset korábban bevezetik.
2. évfolyam a tanulóknak képesnek kell lenniük:
- a 3D alakzatok tulajdonságainak azonosítása és leírása, beleértve az élek, csúcsok és arcok számát
a nem törvényi útmutatás kimondja, hogy:
- a tanulók a közös 2-d és 3-d alakzatok széles skáláját kezelik és nevezik, beleértve a négyszögeket és sokszögeket, valamint a kockákat, prizmákat és kúpokat, és azonosítják az egyes alakzatok tulajdonságait (például az oldalak számát, az arcok számát). A tanulók azonosítják, összehasonlítják és osztályozzák az alakzatokat tulajdonságaik alapján, és pontosan használják a szókincset, például oldalakat, éleket, csúcsokat és arcokat.
ettől a ponttól kezdve a nemzeti tanterv nem hivatkozik ismét kifejezetten a csúcsokra, arcokra és élekre, így a többi évcsoport tanárainak továbbra is ezt a szókincset kell használniuk, amikor az alakra néznek
hogyan kapcsolódnak a csúcsok, arcok és élek a matematika más területeihez?
a diákok a csúcsok, arcok és élek ismeretét használják a 2d-s formák és a 3D-s formák megtekintésekor. A 2D összetett alakzatok kerületének és területének meghatározásához elengedhetetlen az élek ismerete és az összetett alakzatok azonosítása. Fontos alapja a későbbi éveknek, amikor különböző matematikai tételekkel foglalkoznak, mint például a gráfelmélet és a parabolák.
hogyan kapcsolódnak a csúcsok, arcok és élek a való élethez?
a való életben minden tárgynak vannak csúcsai, arcai és élei. Például egy kristály egy oktaéder-nyolc arca, tizenkét éle és hat csúcsa van. Ezeknek a tulajdonságoknak a különböző háromdimenziós formák ismerete megalapozza a különböző iparágakat, mint például az építészet, a belsőépítészet, a mérnöki munka és így tovább.
csúcsok, arcok és élek példa kérdések
1. Magyarázza el, mi a csúcs.
(válasz: egy csúcs az, ahol két vonal találkozik)
2. Hány éle van egy háromszög alakú prizmának?
(válasz: 9)
3. Hány csúcsa van egy kúpnak?
(válasz: 1 csúcs)
4. Hány arca van egy kockának? Milyen 2D-s formák vannak ezeknek az arcoknak?
(válasz: 6 arc. Lehet 2 négyzet alakú és 4 téglalap alakú, vagy csak 6 téglalap alakú.)
5. Az összes közös prizma (kockák, kockák, háromszög alakú prizmák, ötszögletű prizmák és hatszögletű prizmák) összeadja az arcokat és a csúcsokat, és kivonja az éleket. Mit veszel észre a válaszokról?
(válasz: a válasz mindig 2. Ezt Euler-képletnek nevezik (csúcsok száma – élek száma + arcok száma = 2)
kíváncsi arra, hogyan magyarázhatja meg gyermekeinek más kulcsfontosságú matematikai szókincset? Nézze meg elsődleges matematikai szótárunkat, vagy próbálja ki ezeket:
- mi a matematika elsajátítása?
- mik azok a 2d alakzatok?
- mik azok a 3d alakzatok?
rengeteg geometria óravázlatot és nyomtatható munkalapot talál az általános iskolások számára a harmadik tér tanulási matematika hubon.
Online 1-to-1 matematika órák az iskolák és a tanárok megbízásából
minden héten a Third Space Learning matematikai szakoktatói általános iskolás gyermekek ezreit támogatják heti online 1-to-1 órákkal és matematikai beavatkozásokkal. 2013 óta több mint 100 000 gyermeknek segítettünk magabiztosabb, képességesebb matematikusokká válni. Tudjon meg többet, vagy kérjen személyre szabott árajánlatot, hogy beszéljen velünk az Ön igényeiről és arról, hogyan tudunk segíteni.
az online tandíj matematika program biztosítja minden gyermek saját szakmai egy-egy matematika oktató