a 2. Kulcsszakasz osztályozása képezi a négy művelet utolsó részét – a négy alapvető matematikai fogalmat, amelyet a tanulóknak tudniuk kell. Ez a blog segít abban, hogy minden tanulója, évtől 3 évig 6, a sikerhez szükséges bizalommal közelítheti meg a divíziót.
a KS2 matematika részlege a KS1-en tanultakra épül. Végére Y2 diákok a várt szabvány lesz képes felidézni és használni szorzás és osztás tények a 2, 5 és 10 szorzótábla, beleértve felismerve páratlan és páros számok.’
a 3.évfolyam tanárai számára mindig jó ötlet biztosítani, hogy a hallgatók ezeket nagyon jól ismerjék. Ez alatt nem egyszerűen azt értem, hogy a megosztási tényeket rád tudják papagájozni, hanem valóban megértik, hogyan kell ezeket a tényeket konkrét ábrázolásokkal, szóbeli magyarázatokkal és más képi módszerekkel ábrázolni.
azok a diákok, akik nem képesek erre, de képesek szóban elmondani a megosztási tényeket, nagyon sekély megértéssel rendelkeznek a megosztottságról, és ahhoz, hogy a nehezebb problémamegoldó tevékenységekre haladjanak, a megosztottság fogalmi megértésének elmélyítése kötelező a 3.évben.
a Nemzeti Alaptanterv az osztást a szorzással azonos szakaszba helyezi a 3-5.évre, és a 6. év négy műveletének nevezett szakaszba helyezi. A Nemzeti tantervből vett részek csak azokra vonatkoznak, amelyek kifejezetten megemlítik a megosztást. A többi elem ezen szakaszok megtalálható a blog szorzás vagy összeadás és kivonás adott esetben.
Mi A Divízió?
az Osztás egyike a négy műveletnek – a négy alapvető matematikai fogalomnak, amelyeket a tanulóknak ismerniük kell – az összeadás és kivonás, valamint a szorzás mellett.
ahol a szorzás egy szám többszörösét kombinálja, az Osztás az ellenkezője: annak meghatározása, hogy egy szám hányszor van egy másikban. Például a 10-et 2-vel elosztva azt kérdezzük, hogy hányszor van 2 a 10-en belül.

a Third Space Learning Online matematikai beavatkozásaiból.
tanítás osztály KS2-az elmélet
Osztás az inverz szorzás. A szorzás bloghoz hasonlóan a divízió tanítása három mögöttes struktúrát tartalmaz, amelyek, ha megosztási tényekkel és fogalmi megértéssel párosulnak, a diákok a legjobb lehetőséget kapják arra, hogy sikeresek legyenek a divízióval kapcsolatos problémák megoldása során.
a három struktúra a megosztás, a csoportosítás és a méretezés. Bár nincs elég idő, hogy vizsgálja meg ezeket a mélyreható, mi következik lesz csak egy rövid bevezetés őket.
a Megosztás és a csoportosítás a szorzás inverze, mint ismételt összeadás. A megosztás egy strukturális fogalom, amelyet a KS1-ben és korábban vezettek be, ahol, ahogy a neve is sugallja, egy összeget egyenlő csoportokra osztanak.
például 12 almát osztanak meg 3 diák között. Hány almát kap minden diák? Itt tudjuk a teljes összeget (12 alma), és döntő fontosságú, hogy tudjuk, hogyan osztjuk meg az összeget (3). Attól függően, hogy a hallgatók hol vannak matematikai útjukon, többször kivonhatnak valamilyen számmal (1, 2, 3 vagy 4) az összegből három cölöpbe, amelyek a három hallgatót képviselik.
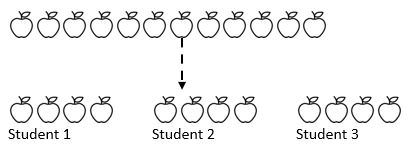
amint a fentiekből láthatjuk, a teljes összeget három egyenlő csoportra osztottuk.
a Csoportosítás hasonló a megosztáshoz, de amit tudunk, kissé eltér a megosztáshoz képest. A megosztási struktúrában tudjuk, hogy hány csoportra kerül sor a megosztásra. A csoportosítási struktúrában tudjuk az egyes csoportok mennyiségét,de nem a tényleges csoportok számát.
például 12 almát osztanak meg 4-es csoportokban. Hány csoport lesz? Bár ez a kérdés nagyon hasonlít a fentiekhez, most átveszi a csoportosítási struktúrát, mivel tudjuk, hogy hányan kerülnek be az egyes csoportokba, de már nem tudjuk, hány csoport lesz most.
mivel tudjuk, hogy minden csoportban 4 van, 4 almát csoportosíthatunk, amíg mind a 12-et lefedjük, hogy lássuk, hogy 3 csoport van.
a felosztás végső szerkezete a méretezés. Míg a szorzás során egy értéket növeltünk, az osztási struktúra lecsökken. Például Shannennek 6 tolla van, jennek pedig 3-szor kevesebb. Hány tolla van jennek?
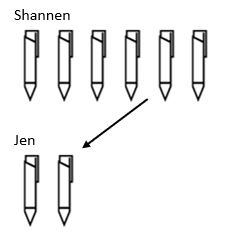
itt láthatjuk, hogy ahhoz, hogy megtaláljuk a Jen tollainak teljes mennyiségét, meg kellett vennünk azt az összeget, amely Shannennek volt, és 3-as méretarányú tényezővel csökkenteni kellett, hogy Jen 2 toll legyen.
a tapasztalatok szerint ez a legnehezebb felosztási struktúra a diákok számára, hogy megértsék és megértsék, és az egyik, amelyet újra kell vizsgálni a skálázással együtt, mint szorzás, mivel ez egy kulcsfontosságú készség, amikor a méréseket és a pénznemeket nagyobb összegről kisebb összegre konvertálják. Pl. kilométer to mérföld.
osztály 3.év
az angliai matematika nemzeti tantervében a matematika minden egyes körvonalazott területén van mind törvényi, mind nem törvényi elem. A törvényi elem a következő:
- Emlékezzünk és használjuk szorzás és osztás tények a 3, 4 és 8 szorzótábla
- Írni és számítani matematikai nyilatkozatok szorzás és osztás segítségével a szorzótábla, hogy tudják, beleértve a kétjegyű számok szorozva egyjegyű számok, a mentális és halad a formális írásbeli módszerek
- problémák megoldására, beleértve a hiányzó szám problémák, bevonásával szorzás és osztás, beleértve a pozitív egész skálázás problémák és levelezés problémák, amelyekben n tárgyak kapcsolódnak m tárgyakat.
jogszabályon kívüli Megjegyzések és útmutatások:
- a tanulók hatékony mentális módszereket fejlesztenek ki, például kommutativitást és asszociativitást (például, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) szorzási és osztási tények (például 3 × 2 = 6, 6 ÷ 3 = 2 és 2 = 6 (3) a kapcsolódó tények levezetésére (például, 30 × 2 = 60, 60 ÷ 3 = 20 és 20 = 60 6db.).
- a tanulók megbízható írásbeli módszereket fejlesztenek ki a szorzáshoz és osztáshoz, kezdve a kétjegyű számok egyjegyű számokkal történő kiszámításával és a rövid szorzás és osztás formális írásbeli módszereivel.
- a tanulók egyszerű problémákat oldanak meg kontextusban, eldöntve, hogy a négy művelet közül melyiket és miért használják. Ezek közé tartoznak a mérési és méretezési összefüggések (például négyszer olyan magas, nyolcszor olyan hosszú stb.) és levelezési problémák, amelyekben m objektumok kapcsolódnak n objektumhoz (például 3 kalap és 4 kabát, hány különböző ruha?; 12 édesség egyenlően oszlik meg 4 gyermek között; 4 sütemény egyenlően oszlik meg 8 gyermek között).
Osztálytevékenységek 3.év
ez önmagában nem terjed ki egy leckére, hanem útmutatást nyújt arról, hogyan lehet a divíziót bizonyos fogalmi megértéssel tanítani ebben a szakaszban. Ennek előfeltétele lenne a kapcsolódó szorzási tények tanítása, mielőtt bármilyen kapcsolódó felosztást tanítanának.
amikor a struktúrákra gondolunk, a diákok tanulási útjának ezen részén a legjobb, ha a csoportosításhoz és a megosztáshoz ragaszkodunk. A következő példákhoz, megvizsgáljuk, hogy a hallgatók megértsék-e az osztást 4. A konkrét-képi-absztrakt megközelítést követi.
gyakran a diákok számának megértése korlátozhatja a divízió előrehaladását. Különösen akkor, ha csoportosításról és megosztásról van szó, amikor csak az egyiket veszik el folyamatosan az egészből.
a tanítási osztály kezdetétől fogva a tanároknak arra kell támaszkodniuk, amit a diákok már tudnak a páros számokról és más számtényezőkről, hogy a diákokat a megfelelő számban számolják.
a számlálók felhasználhatók a kapcsolódó megosztási tények bemutatására, mivel a hallgatók téziseket használnak a szorzás fogalmi megértésének felépítésekor. Kérdések, mint például, ‘ hány csoport 4 vannak? és hányan vannak az egyes csoportokban? meg kell kérdezni, és a válaszoknak arra kell vonatkozniuk, hogy ez hogyan mutatja a megosztottságot.
tanár: hány számláló van?
Gyermek: Négy
Tanár: Jó. Ez egy négyes csoport. Hány Négyes csoport van?
Gyermek: Egy
Tanár: Kiváló. Négy számlálónk van egy csoportban. Négy számlálót csoportosítottunk egy csoportba. Mit tettünk?
gyermek: négy számlálót csoportosított egy csoportba.
Tanár: Ragyogó. Amikor négy számlálót egy csoportba csoportosítunk, elvégeztük a négy matematikai számítását osztva eggyel. Milyen számításokat végeztünk?
gyermek: négy osztva eggyel.
Mester: és amikor megoldjuk a négyet osztva eggyel, a válasz négy, mert létrehoztunk egy csoportot, amelyben négy elem van. Négy osztva eggyel, az Négy. Mi a négy osztva eggyel?
gyermek: Négy osztva eggyel, az Négy.
tanár: kiváló
láthatja, hogy ez hogyan ismétlődne meg a következőknél:
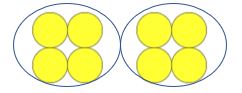
tanár: hány számláló van?
gyermek: nyolc
tanár: jó, ez egy négyes csoport. Hány Négyes csoport van?
Gyermek: Két
Tanár: Kiváló. Négy számlálónk van egy csoportban. Négy számlálót két csoportba csoportosítottunk. Mit tettünk?
gyermek: négy számlálót két csoportba csoportosított.
Tanár: Ragyogó. Amikor négy számlálót két csoportba csoportosítunk, elvégeztük a nyolc matematikai számítását osztva kettővel. Milyen számításokat végeztünk?
gyermek: nyolc osztva kettővel.
Mester: és amikor megoldjuk a nyolcat osztva kettővel, a válasz négy, mert két csoportot hoztunk létre, amelyekben négy elem van. Nyolc osztva kettővel, az Négy. Mi a nyolc osztva kettővel?
gyermek: nyolc osztva kettővel négy.
tanár: kiváló
amikor a diákok kezdenek magabiztossá válni ezzel, áttérhetünk más modellekre, például a Cuisenaire rudakra.

itt a teljes összeg képviselteti magát a felső vonat és a purple rod (ami ebben az esetben jelentése 4 és ha elolvasta más blogok ebben a sorozatban remélhetőleg tudni fogja, hogy mennyi egy szószólója vagyok azok használatát az osztályteremben, és így a diákok tisztában lesznek annak értékét addigra) használják, hogy hány csoport 4 mehet be a teljes összeget.
a diákok ezután továbbléphetnek a tanár által olvasott forgatókönyvek rajzolásához. Például. 24 gomb van, amelyeket 4-Be kell csoportosítani. Hány csoport van? A diákok felhívhatják ezeket a gombokat, és csoportosíthatják őket 4 stb.
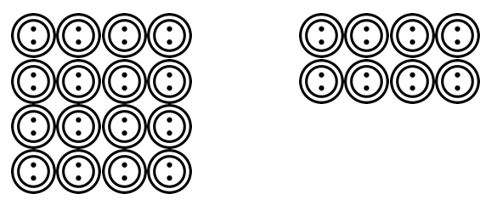
miután a diákok megszokták, hogy képesek megjeleníteni ezeket a csoportosítási vagy megosztási forgatókönyveket számos kontextusban, akkor matematikai szimbólumok segítségével továbbhaladhatnak az elvontabb ábrázolásokra.

3 hosszú osztású munkalapok 3-6 évig
készítse elő a tanulóit a hosszú osztásra a KS2-ben ezekkel a hosszú osztású munkalapokkal.
3. év
a 3.év Szóproblémái általában a csoportosítási vagy megosztási struktúrát használják.
40 sütemény és 10 diák van. Hány süteményt kap minden diák?
mivel tudjuk, hogy hány csoport van (10), ki kell dolgoznunk a csoportonkénti összeget, tehát ez egy megosztási struktúra. A diákok elvárják, hogy használja a tudásukat a 4-szeres táblázat, hogy dolgozzanak ki, és kap a válasz 4.
körzet: Érvelés és problémamegoldás 3. év
érvelés és problémamegoldás szempontjából jó tevékenységnek találom, ha egy szóproblémát egy számításhoz illesztek. Például:
illessze össze a 20 osztva 4-gyel megoldott szóproblémákat.
- 20 ceruza van, amelyeket 5-ös csomagokba kell helyezni. Hány van egy csomagban?
- 20 ceruza volt, majd egy diák még 4-et hoz be. Hány ceruza van most?
- 20 ceruza van, és 4 darabos csomagokba kerülnek. Hány van egy csomagban?
- 20 ceruza volt, majd 4 eltűnt. Hány ceruza van most?
hasznos, ha a hallgatók minden kérdésre leírják magyarázataikat, mivel ez lehetővé teszi gondolkodásuk megismerését. A kérdéseket gondosan választották ki, hogy az egyes kérdések számai a kérdés számaihoz kapcsolódjanak, így a hallgatók matematikai készségeikre támaszkodva levezetik a helyes választ.
4.osztály év
az angliai matematika nemzeti tantervében a felvázolt matematika minden területén van mind törvényi, mind nem törvényi elem. A törvényi elem a következő:
- emlékezzünk szorzás és osztás tények szorzótábla legfeljebb 12 62
- használja helyérték, ismert és származtatott tények szorozni és osztani mentálisan, beleértve: szorozva 0 és 1; elosztjuk 1; szorozva együtt három szám
nem kötelező Megjegyzések és útmutatás:
- a tanulók továbbra is gyakorolják a szorzótáblák és a kapcsolódó osztási tények felidézését és használatát a folyékonyság elősegítése érdekében.
- a tanulók mentális módszereket alkalmaznak, és ezt háromjegyű számokra is kiterjesztik a tények levezetése érdekében (például 600 3 = 200 2 x 3 = 6-ból származtatható).
- a tanulók gyakorolják, hogy folyékonyan elsajátítsák a rövid szorzás és a rövid Osztás formális írásbeli módszerét pontos válaszokkal
- a tanulók kétlépcsős problémákat oldanak meg kontextusban, kiválasztva a megfelelő műveletet, egyre nehezebb számokkal dolgozva. Ennek tartalmaznia kell a levelezési kérdéseket, például az étkezés választásának számát egy menüben, vagy három sütemény egyenlően oszlik meg 10 gyermekek.
osztály lecke ötletek 4.év
ehhez a leckéhez azt fogom megvizsgálni, hogyan kezdheti el a rövid Osztás tanítását manipulatív eszközökkel.
mondjuk fogunk tanítani a diákok rövid osztály a kérdés 168 osztva 12.
általában ezt írnánk az úgynevezett buszmegállóban. De ami érdekes,hogy a világ különböző helyei másképp írják.
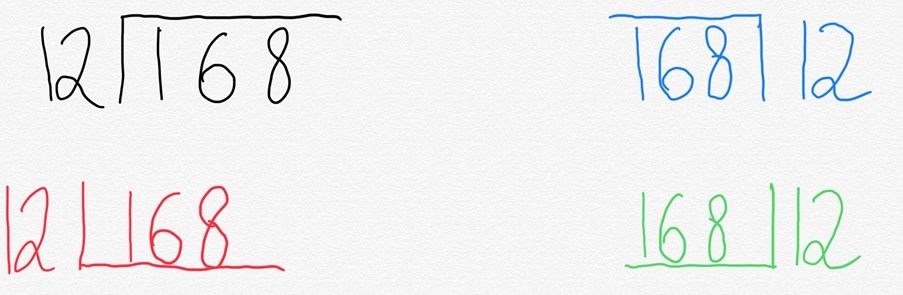
ennek oka meglehetősen egyszerű. Amit a’ buszmegálló ‘ valójában képvisel, az egy téglalap ábrázolásának rövidített módja.
amikor formális rövid felosztást tanítunk, akkor azt mondjuk, hogy el kell képzelni egy téglalapot, ahol a szélesség 12. A téglalap teljes területe 168, és megpróbáljuk megtalálni a hiányzó hosszúságot a tetején. Tehát hogyan mutathatjuk meg ezt manipulatív eszközökkel? A Dienes blokkok hasznos eszköz erre.
tudjuk, hogy a teljes összeg 168. Tehát össze kell gyűjtenünk 168 értékű diéneket a lehető legkisebb mennyiségű blokk felhasználásával. Ez az alábbiakban látható.
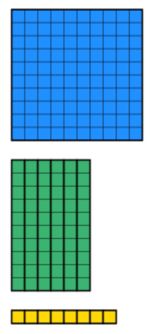
Visszatekintve a kérdésre, tudjuk, hogy a szélesség 12. Ez azt jelenti, hogy most kell manipulálni a blokkokat, hogy megkapjuk a szélessége 12. Ne feledje, hogy a téglalapnak szilárdnak kell lennie, és nem lehetnek hiányzó részei. Például az alábbiak nem engedélyezettek annak ellenére, hogy 12 egység megy le a szélességen.
ehelyett a diákok két 10S blokkot forgathatnak, hogy megkapják a következőket. Figyeljük meg, hogy van 12 minden oszlopban, és ez egy szilárd tárgy.
az utolsó rész, amelyet a hallgatóknak meg kell tenniük, a fennmaradó blokkok felhasználásával eladott téglalapot hoznak létre, miközben megtartják a 12 szélességet. Ez eltarthat egy ideig, de a gyakorlat, a diákok nem kap gyorsabb. Egy idő után a hallgatók ezt előállítják:
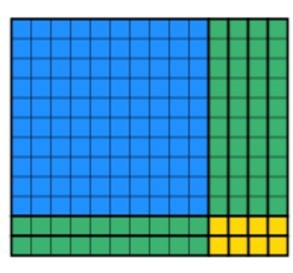
láthatjuk, hogy mind a 168 értékű tömböt felhasználták, és hogy a szélesség még mindig 12. A válasz megtalálásához a hallgatóknak meg kell számolniuk a hosszúságot, amely ebben az esetben 14. Az alábbiakban mindkét módszert egymásra helyeztem, így láthatja, hogyan egészítik ki egymást az alábbiakban.
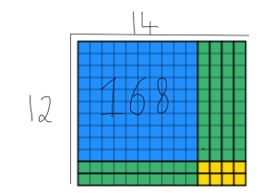
ez egy hasznos stratégia a hallgatók tanítására a 4. évben, mivel a tanterv más területein hatalmas visszahatások vannak, amelyek már megvilágítottak a hallgatók számára.
bár lehet, hogy még nem ismerik fel, az ilyen rövid felosztás tanításával már bevezették őket a kerületbe és a területre – gondolja meg, mennyi tanítási időt lehet megtakarítani, ha ez a kapcsolat létrejön. Nem csak ez, hanem másodlagosan ez a megközelítés átkerül az algebrai gondolkodásra.
Division Word problémák 4.év
a diákok várhatóan felhívni tudásukat helyérték megoldani osztály alapú problémák, és így egy megfelelő szót probléma lenne.
egy gyümölcsös 4800 almát termesztett egy szezonban. A piacra lépés előtt 4 darabos csomagolásban kerülnek forgalomba. Hány csomag van?
itt a diákok kell használni azt a tényt, hogy 4 x 12 = 48 és mivel 4800 százszor több, mint 48, 12 is meg kell szorozni 100, hogy 1200
osztály: Érvelés és problémamegoldás 4. év
mindig, néha vagy soha nem igaz, hogy három páros szám összege osztható 4-gyel?
ez a kérdés bőséges lehetőséget ad a hallgatóknak arra, hogy kísérletezzenek a kérdés paraméterein belül. Azok a diákok, akiknek több támogatásra van szükségük, megnézhetik a Sing digit páros számokat, és a diákok bármit is elérhetnek, amit jól érzik magukat.
a nyitott kérdések, mint ez, ez jó, hogy egy minimális követelmény, hogy hány kísérletet diákok kell tennie, különben gyakran úgy dönt, hogy nem a minimum.
a válasz erre a kérdésre néha.
egy gyors ‘trükk’ annak megállapítására, hogy egy szám osztható-e, ha megnézzük a szám utolsó 2 számjegyét, és megnézzük, hogy azok oszthatók-E 4-gyel. Például, ha egy gyermek megtalálta a 34, 36 és 38 összegét, és 108-at kapott, tanárként tudom, hogy ez a szám osztható 4-gyel, mivel az utolsó két számjegy (08) 8-at tesz ki, és osztható 4-gyel. Ha egy gyermek a 34 – et, a 36 – ot és a 48-at választotta a 118-hoz, akkor tudom, hogy ez nem osztható 4-gyel, mivel a 18-a 118 utolsó két számjegye-nem osztható 4-gyel.
5.osztály
az angliai matematika nemzeti tantervében a felvázolt matematika minden területén van mind törvényi, mind nem törvényi elem. A törvényi elem a következő:
- szorozzuk meg és osszuk el a számokat mentálisan ismert tények alapján
- osszuk el a számokat legfeljebb 4 számjegyig egyjegyű számmal a rövid Osztás formális írásbeli módszerével, és értelmezzük a maradványokat a kontextusnak megfelelően
- szorozzuk és osztjuk meg az egész számokat és a tizedesjegyeket 10, 100 és 1000
- oldja meg a szorzással és osztással kapcsolatos problémákat, beleértve a tényezők és osztások ismeretének felhasználását szorzók, négyzetek és kockák
- az összeadással, kivonással, szorzással és osztással kapcsolatos problémák megoldása, valamint a következők kombinációja ezek, beleértve a
- egyenlőségjel jelentésének megértését, megoldják a szorzással és osztással kapcsolatos problémákat, beleértve az egyszerű törtekkel történő skálázást és az egyszerű arányokkal kapcsolatos problémákat.
jogszabályon kívüli Megjegyzések és útmutatások:
- a tanulók az osztásra adott nem egész válaszokat úgy értelmezik, hogy az eredményeket a kontextus szerint különböző módon fejezik ki, beleértve a maradékokat is, törtként, tizedesjegyként vagy kerekítéssel (például 98 6.számú = = 24 r 2 = 24 = 24,5 25. számú).
- a tanulók inverzként használják a szorzást és az osztást, hogy támogassák az arány bevezetését a 6.évben, például a 10-es hatványokkal való szorzással és osztással a skála rajzokon, vagy az 1000-es hatványokkal való szorzással és osztással az egységek, például a kilométer és a méter közötti átváltáskor.
osztály tevékenységek 5.év
az 5. év osztályozása a válaszok maradványainak felhasználásával halad előre. Ehhez a leckéhez egy másik felhasználási manipulatívumot fogok megvizsgálni, amelyet a tanárok felhasználhatnak a 4-by-1 számjegyű Osztás tanítására.
ha a kérdés 5642 osztva 4-gyel, akkor ezt egy helyérték-diagram és helyérték-számlálók segítségével ábrázolhatjuk, amint azt alább láthatjuk.
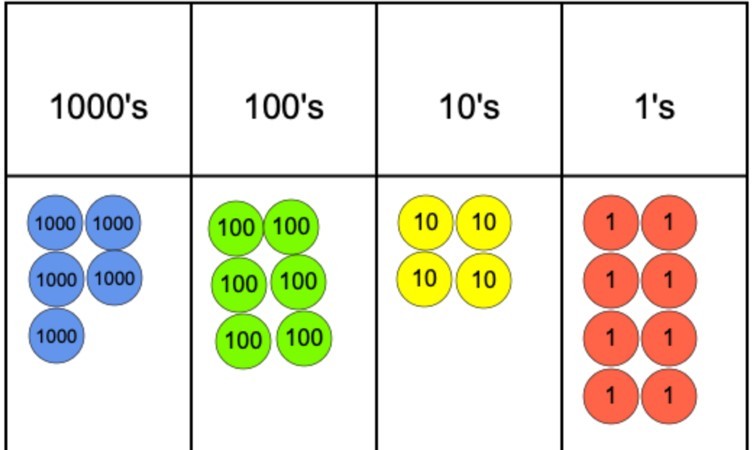
a következő lépés az lenne, hogy elkezdjük csoportosítani a számlálókat 4-re, mivel ez az osztónk. Amint azonban látható, gyorsan problémához jutunk az 1000-es oszlopban, mivel képesek vagyunk a számlálók 4-es csoportosítására, de akkor nem tudjuk csoportosítani a fennmaradó számlálót egy 4-es csoportba.
a probléma leküzdése érdekében az 1000 számláló, amelyet nem csoportosítottak, tíz 100 számlálóra cserélhető. Ezeket 4-es csoportokba lehet csoportosítani, és ez megtörténhet anélkül, hogy 100-as számlálók maradnának. Onnan, ez egy egyszerű eset, amikor a 10-es évekbe, végül pedig azokba költözünk.
mivel kilenc 1S számláló van, 8-at csoportosíthatunk 2 csoportba és 4-be, és azt állíthatjuk, hogy van még egy*. A válasz megtalálásához mindössze annyit kell tennie, hogy megszámolja az egyes helyértékekben létrehozott csoportok számát, és ezekkel írja be a számjegyeket a végső válasz létrehozásához. Ebben az esetben a válasz 1412 maradék 1 lenne.
* ha tizedesjegyeket néz, akkor a fennmaradó 1S számlálót tíz 0,1 számlálóra cserélheti, és folytathatja a felosztást a fent leírtak szerint. A diákok, hogy ismeri ezt a modellt hasznos, mert segíthet demisztifikálni osztály tizedesjegyekkel, amelyek a diákok küzdenek. Ez segít nekik látni, hogy ez egy olyan folyamat folytatása, amelyet már ismernek, nem pedig valami újat.
Division problémák 5.év
amikor elosztjuk az 5. év, a diákok találkoznak forgatókönyvek, ahol meg kell kerekíteni a választ fel annak érdekében, hogy a válasz, hogy van értelme a kontextusban. Egy megfelelő kérdés, amely ezt bizonyítja, a következő lenne:
egy iskola társadalmi távolságtartó diszkót tervez, ahol azt tervezik, hogy minden hallgatónak 250 ml gyümölcslevet kínálnak. Vásárolhatnak 2 literes üveg gyümölcslevet. 33 diák érkezését várják, így tudják, hogy 8,25 liter gyümölcslevet adnak ki. Hány üveg gyümölcslevet kell vásárolni?
általános válasz, hogy a diákok 4-et és negyedet mondanak. Azonban, mivel nem lehet egy negyed palackot vásárolni, ebben az esetben a helyes válasz az lenne 5 üveg gyümölcslé lenne szükség annak biztosítására, hogy minden diák részt vehessen.
osztály: érvelés és problémamegoldás 5. év
mint fentebb megjegyeztük, az 5.évben a diákok a divízión belüli forgatókönyvekkel találkoznak, ahol meg kell választaniuk, hogy a választ felfelé vagy lefelé kell-e kerekíteni. Például, amikor egy kérdés arra kéri a diákokat, hogy dolgozzanak ki, hány buszra van szükség egy iskolai utazáshoz.
az, hogy a hallgatók saját problémákat hozzanak létre a megadott kontextus használatával, valóban kihívást jelentő tevékenység lehet, amely a diákokat matematikailag gondolkodik a kontextusról és a megosztásról.
a diákok ezután kicserélhetik ezeket a kérdéseket, amelyeket létrehoztak egy partnerrel, majd megoldhatják őket, és ellenőrizhetik az eredeti kérdéskészítővel, hogy helyes-e a válasz.
6.osztály
az angliai matematika nemzeti tantervében a felvázolt matematika minden területén van mind törvényi, mind nem törvényi elem. A törvényi elem a következő:
- osszuk el a számokat legfeljebb 4 számjegyig egy kétjegyű egész számmal a hosszú osztás formális írásbeli módszerével, és értelmezzük a maradványokat egész számmaradékként, törtként vagy kerekítéssel, a kontextusnak megfelelően
- osszuk el a számokat legfeljebb 4 számjegyig kétjegyű számmal a rövid Osztás formális írásbeli módszerével, ahol szükséges, értelmezzük a maradványokat a kontextus szerint
- végezzen mentális számításokat, beleértve a vegyes műveleteket és a nagy számokat
- közös tényezők, közös szorzók és prímszámok azonosítása
- a műveletek sorrendjével kapcsolatos ismereteik felhasználásával végezzen számításokat a négy művelettel
nem jogszabályban előírt Megjegyzések és útmutatások:
- az összeadással, kivonással, szorzással és osztással kapcsolatos problémák megoldása
- használja a becslést a számítások válaszainak ellenőrzésére és a probléma összefüggésében a megfelelő pontosság meghatározására.
osztály lecke ötletek 6.év
Sophie Bartlett (@_MissieBee) kiváló blogot hozott létre itt (link Sophie blogjához a hosszú osztály tanításáról), amely részletezi, hogyan tanítana hosszú osztályt egy 6. évfolyamon. Mivel a long division az egyetlen új tanulás a 6. évfolyamon, ez ideális módszer a long division eljárás bevezetésére.
osztály kérdések 6.év
egy tipikus osztály szó probléma, hogy egy év 6 diák is találkoznak lenne:
egy iskola emelt 3,146 egy bake sale. 104 szülő vett részt az eseményen. Ha minden szülő egyenlő összeget költött, mennyit költött minden szülő?
itt a diákok elvárják, hogy a hosszú osztás módszer, hogy megoldja ezt a kérdést, hogy a választ 60,25.
osztály: érvelés és problémamegoldás 6.év
valami eljárási, mint a hosszú osztály, egy jó érvelési tevékenység az, hogy a diákok hibákat találnak. Ezek az erőforrások az ilyen tevékenységek nagy bankját biztosítják. Amint az alábbi kérdésből láthatjuk, a diákok minden kemény munkát elvégeztek, de egy gondatlan hiba az 59-es csoportok számlálásakor azt jelentette, hogy a gyermek úgy gondolta, hogy az 59 x 7 472, nem pedig 59 x 8.
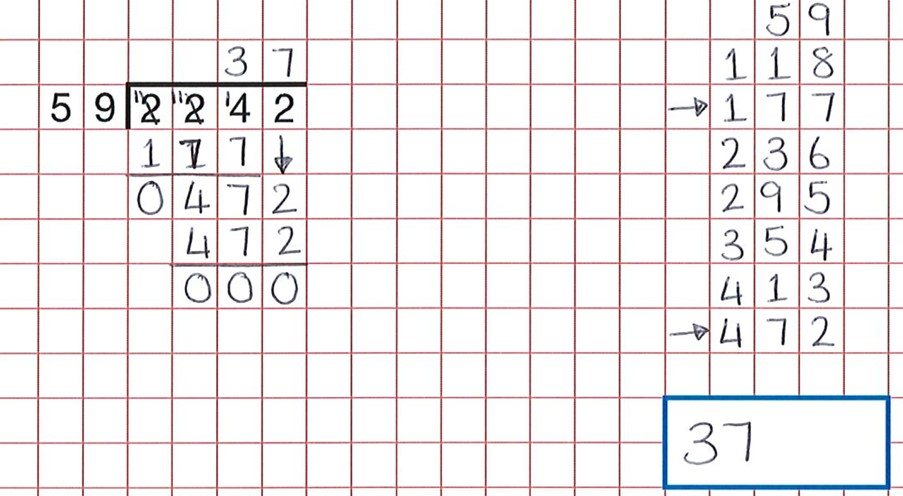
a helyes válasz 38 lett volna.
a Divízió kulcsfontosságú matematikai téma, nem csak a KS2-nél, hanem a matematika egészében is. Remélhetőleg ez a bejegyzés jó ötleteket adott neked, amelyek segítenek a tanulóknak magabiztosan megközelíteni.
Online 1-to-1 matematika órák az iskolák és a tanárok megbízásából
minden héten a Third Space Learning matematikai szakoktatói általános iskolás gyermekek ezreit támogatják heti online 1-to-1 órákkal és matematikai beavatkozásokkal. 2013 óta több mint 100 000 gyermeknek segítettünk magabiztosabb, képességesebb matematikusokká válni. Tudjon meg többet, vagy kérjen személyre szabott árajánlatot, hogy beszéljen velünk az Ön igényeiről és arról, hogyan tudunk segíteni.
az általános iskolai oktatás az egyes gyermekek igényeire irányul, és szorosan követi a Nemzeti tantervet.