neste guia, explicarei Qual é a fórmula de erro padrão e como usá-la para resolver o erro padrão por meio do uso de um exemplo.
Qual é o erro padrão?
O erro padrão (SE), às vezes referido como o erro padrão da média (SEM), é uma estatística que corresponde ao desvio padrão de uma amostra da distribuição, em relação ao valor médio. Mas o que realmente é isso?
dizem que você está interessado na Idade Média, as pessoas no Reino Unido são diagnosticadas com a doença de Alzheimer. Não é viável determinar isso para todos no Reino Unido, portanto, os pesquisadores coletam uma população de amostra para generalizar um número geral. Por exemplo, 10.000 britânicos com a doença podem ser analisados e serão usados para gerar a idade média do diagnóstico. Se você fizer isso em uma amostra aleatória de 5.000 pacientes, você pode obter uma idade média de diagnóstico de 61,5 anos. No entanto, se você fizer a análise da amostra em uma amostra aleatória separada de 10.000 outros pacientes, poderá ter uma idade média de 62,3 anos. Digamos, hipoteticamente falando, é claro, que se você fosse capaz de analisar todas as pessoas no Reino Unido que têm a doença de Alzheimer para obter o número real, você pode acabar com 64,3 anos. Você pode notar que os números obtidos das populações amostrais (61,5 e 62,3 anos) diferem do valor real (64,3 anos). Essa variação nos valores médios é esperada e, à medida que você aumenta o número de pessoas em sua população de amostra, obtém um valor mais próximo do valor real. É exatamente isso que o erro padrão representa. O erro padrão significa essa variação nos valores médios entre as populações da amostra.
para uma leitura mais aprofundada, sugiro que você leia a breve nota estatística dos professores Douglas Altman e Martin Bland publicada no British Medical Journal. É uma visão útil sobre o que é o erro padrão e qual é a diferença com o desvio padrão.
A fórmula de erro padrão
para calcular o erro padrão, você precisa ter duas informações: o desvio padrão e o número de amostras no conjunto de dados. O erro padrão é calculado dividindo o desvio padrão pela raiz quadrada do número de amostras.
aqui está a fórmula de erro padrão anotada completa:
exemplo
para entender melhor a fórmula de erro padrão, pode ajudar a passar por um exemplo. Digamos que temos uma população de 80 pessoas e estamos interessados em sua altura. Medimos sua altura e calculamos o desvio padrão como 30,6 cm. Agora precisamos conectar esses valores em nossa equação:
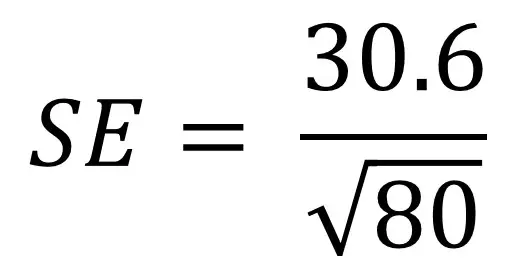se você está desconfortável com a introdução de equações em calculadoras, você pode quebrar a fórmula em pedaços gerenciáveis. Aqui estão os passos que você pode tomar.
- em primeiro lugar, calcule a raiz quadrada do número de amostras (n). Neste caso, n é 80. A raiz quadrada de 80 é 8,94.
- em seguida, divida o desvio padrão (30,6) pela raiz quadrada de 80 (8,94). Fazer isso dá um valor de 3,42.
- portanto, o erro padrão em nossa população de altura é de 3,42 cm.