Divisão no Key Stage 2 formas, a última parte do “Quatro Operações” – os quatro principais conceitos matemáticos os alunos devem saber. Este blog irá ajudá-lo a garantir que todos os seus alunos, do ano 3 ao ano 6, possam abordar a divisão com a confiança de que precisam para ter sucesso.
a divisão em matemática KS2 baseia-se no que foi aprendido no KS1. No final do Y2, os alunos no padrão esperado poderão ” recordar e usar Fatos de multiplicação e divisão para as tabelas de multiplicação 2, 5 e 10, incluindo o reconhecimento de números ímpares e pares.’
para professores no ano 3, é sempre uma boa ideia garantir que os alunos os conheçam muito bem. Com isso, não quero dizer simplesmente que eles possam papagaio os fatos de divisão em você, mas eles realmente entendem como representar esses fatos tanto com representações concretas, explicações verbais e através de outros métodos pictóricos. Alunos que não são capazes de fazer isso, mas são capazes de dizer verbalmente os fatos da divisão, têm uma compreensão muito superficial da divisão e para que eles progridam em atividades de resolução de problemas mais difíceis, aprofundar sua compreensão conceitual da divisão é uma obrigação no ano 3.
o currículo nacional coloca a divisão dentro da mesma seção que a multiplicação para os anos 3-5 e a coloca dentro de uma seção chamada ‘Quatro Operações’ no ano 6. As partes retiradas do Currículo Nacional referem-se apenas àquelas que mencionam especificamente a divisão. Os outros elementos dessas seções podem ser encontrados no blog sobre multiplicação ou adição e subtração, quando apropriado.
O Que É Divisão?
a divisão é uma das Quatro Operações – os quatro principais conceitos matemáticos que os alunos devem conhecer-juntamente com adição e subtração e multiplicação.
onde a multiplicação está combinando um número várias vezes, a divisão é o oposto: descobrir quantas vezes um número está contido em outro. Por exemplo, dividir 10 por 2 é perguntar quantas vezes 2 está contido dentro de 10.

das intervenções matemáticas online da Third Space Learning.
Divisão de ensino KS2-a teoria
divisão é o inverso da multiplicação. Tal como acontece com o blog de multiplicação, o ensino da divisão contém três estruturas subjacentes, que, quando combinadas com Fatos de divisão e compreensão conceitual, darão aos alunos a melhor oportunidade de ter sucesso ao resolver problemas relacionados à divisão.
as três estruturas estão compartilhando, agrupando e escalando. Embora não haja tempo suficiente para explorá-los em profundidade, o que se segue será apenas uma breve introdução a eles.
compartilhar e agrupar são o inverso da multiplicação como adição repetida. O compartilhamento é um conceito estrutural introduzido no KS1 e anterior, onde, como o nome sugere, um valor é compartilhado em grupos iguais.
por exemplo, 12 maçãs são compartilhadas entre 3 alunos. Quantas maçãs cada aluno recebe? Aqui sabemos a quantidade total (12 maçãs) e, crucialmente, sabemos como a quantidade em que vamos compartilhar (3). Dependendo de onde os alunos estão em sua jornada matemática, eles podem subtrair repetidamente por algum número (1, 2, 3 ou 4) do valor em três pilhas que representam os três alunos.
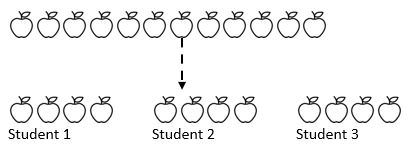
como podemos ver acima, o valor total foi compartilhado em três grupos iguais.
o agrupamento é semelhante ao compartilhamento, mas o que sabemos é um pouco diferente quando comparado ao compartilhamento. Na estrutura de compartilhamento, sabemos a quantidade de grupos que o compartilhamento ocorrerá. Na estrutura de agrupamento, sabemos o valor em cada grupo, mas não o número de grupos reais que existem.
por exemplo, 12 maçãs são compartilhadas em grupos de 4. Quantos grupos haverá? Embora esta questão seja muito semelhante à acima, agora assume a estrutura de agrupamento, pois sabemos quantos entrarão em cada grupo, mas não sabem mais quantos grupos haverá agora. Como sabemos que existem 4 em cada grupo, podemos agrupar 4 maçãs até Termos coberto todos os 12 para ver que existem 3 grupos.
a estrutura final da divisão é escalonada. Enquanto na multiplicação estávamos aumentando um valor, a estrutura de divisão diminui. Por exemplo, Shannen tem 6 Canetas e Jen tem 3 vezes menos. Quantas Canetas Jen tem?
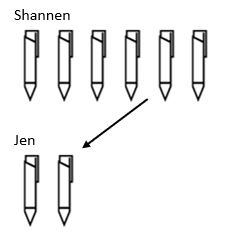
Aqui podemos ver que para encontrar o valor total de canetas que Jen tem, tivemos que tomar a quantidade que Shannen tinha e redução por um fator de escala de 3 de modo que Jen acaba com 2 canetas.
por experiência própria, esta é a estrutura de divisão mais difícil para os alunos compreenderem e compreenderem e é aquela que precisa ser revisitada em conjunto com a escala como multiplicação, pois esta é uma habilidade crucial ao converter medições e moedas de uma quantidade maior para uma quantidade menor. Por exemplo, quilômetros a milhas.
ano de Divisão 3
no Currículo Nacional de matemática na Inglaterra, para cada área de matemática delineada, existe um elemento estatutário e um elemento não estatutário. O elemento estatutário é o seguinte:
- recuperar e usar a multiplicação e a divisão de fatos para os 3, 4 e 8 tabelas de multiplicação
- Escrever e calcular matemática instruções de multiplicação e divisão, utilizando as tabelas de multiplicação que eles sabem, inclusive para números de dois dígitos vezes um dígito, usando mental e avançar para a escrita formal, métodos de
- Resolver problemas, incluindo a falta de número de problemas que envolvem a multiplicação e a divisão, incluindo inteiro positivo problemas de escala e a correspondência problemas em que n objetos estão conectados a m objetos.
Não-estatutárias e notas de orientação:
- os Alunos a desenvolver mentais eficazes métodos, por exemplo, usando commutativity e associatividade ‘ (por exemplo,, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) e, multiplicação e divisão de números (por exemplo, usando 3 × 2 = 6, 6 ÷ 3 = 2 e 2 = 6 ÷ 3) para derivar relacionadas a fatos (por exemplo,, 30 × 2 = 60, 60 ÷ 3 = 20 e 20 = 60 ÷ 3). Os alunos desenvolvem métodos escritos confiáveis para multiplicação e divisão, começando com cálculos de números de dois dígitos por números de um dígito e progredindo para os métodos escritos formais de multiplicação e divisão curtas.
- os alunos resolvem problemas simples em contextos, decidindo qual das quatro operações usar e por quê. Isso inclui contextos de medição e dimensionamento (por exemplo, quatro vezes mais alto, oito vezes mais longo etc.) e problemas de correspondência em que M objetos estão conectados a n objetos (por exemplo, 3 Chapéus e 4 Casacos, quantas roupas diferentes?; 12 doces compartilhados igualmente entre 4 crianças; 4 bolos compartilhados igualmente entre 8 crianças).
atividades de divisão ano 3
isso não cobrirá uma lição em si, mas fornecerá um guia sobre como a divisão pode ser ensinada com algum entendimento conceitual nesta fase. Um pré-requisito para isso seria o ensino de fatos de multiplicação relacionados antes de ensinar qualquer divisão relacionada.
ao pensar em estruturas, é melhor nesta parte da jornada de aprendizagem dos alunos manter o agrupamento e o compartilhamento. Para os exemplos a seguir, analisaremos o desenvolvimento da compreensão dos alunos de dividir por 4. Seguirá a abordagem Concreto-pictórica-abstrata.
muitas vezes, é a compreensão do número pelos alunos que pode limitar seu progresso na divisão. Particularmente quando se trata de agrupar e compartilhar quando eles apenas tiram um continuamente do todo. Desde o início da Divisão de ensino, os professores devem se apoiar no que os alunos já sabem sobre números pares e outros fatos numéricos para levar os alunos a contar em qualquer número que possa ser apropriado.
contadores podem ser usados para demonstrar Fatos de divisão relacionados, pois os alunos terão usado teses ao construir sua compreensão conceitual da multiplicação. Perguntas como: ‘quantos grupos de 4 existem?’e’ quantos há em cada grupo?’deve ser perguntado e as respostas devem se relacionar com a forma como isso mostra a divisão.
Professor: quantos contadores existem?
Criança: Quatro
Professor: Bom. Este é um grupo de quatro. Quantos grupos de quatro existem?
Criança: Um
Professor: Excelente. Temos quatro contadores em um grupo. Agrupamos quatro contadores em um grupo. O que fizemos?
criança: agrupou quatro contadores em um grupo.
Professor: Brilhante. Quando agrupamos quatro contadores em um grupo, fizemos o cálculo matemático de quatro divididos por um. Que cálculo fizemos?
criança: quatro divididos por um.Professor: e quando resolvemos quatro divididos por um, a resposta é quatro porque fizemos um grupo que tem quatro itens nele. Quatro divididos por um são quatro. O que é quatro dividido por um?
criança: Quatro divididos por um são quatro.
Professor: Excelente
Você pode ver como isso iria ser repetido para o seguinte:
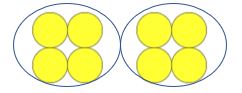
Professor: Como muitos contadores estão lá?
criança: oito
Professor: bom, este é um grupo de quatro. Quantos grupos de quatro existem?
Criança: Dois
Professor: Excelente. Temos quatro contadores em um grupo. Agrupamos quatro contadores em dois grupos. O que fizemos?
criança: agrupou quatro contadores em dois grupos.
Professor: Brilhante. Quando agrupamos quatro contadores em dois grupos, fizemos o cálculo matemático de oito dividido por dois. Que cálculo fizemos?
criança: oito dividido por dois.
professor: e quando resolvemos oito dividido por dois, a resposta é quatro porque fizemos dois grupos que têm quatro itens nele. Oito dividido por dois é quatro. O que é oito dividido por dois?
criança: oito dividido por dois é quatro.
Professor: Excelente
Quando os alunos estão começando a ficar confiante com isso, podemos passar para outros modelos, tais como varas de Cuisenaire.

Aqui todo o valor é representado em cima do trem e o roxo da haste (que neste caso representa 4 e se você ler outros blogs nesta série, esperamos que você vai saber o quanto de um advogado, eu sou para o seu uso na sala de aula e para os alunos conscientes do seu valor, em seguida,) é usada para mostrar como muitos grupos de 4, pode ir para o montante total.
os alunos podem então passar para desenhar cenários lidos pelo professor. Por exemplo. Existem 24 botões e eles precisam ser agrupados em 4. Quantos grupos existem? Os alunos podem desenhar esses botões e agrupá-los em 4 etc.
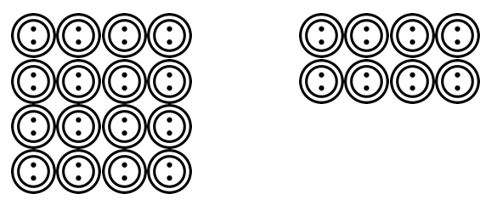
uma vez que os alunos se acostumaram a visualizar esses cenários de divisão de agrupamento ou compartilhamento em uma variedade de contextos, eles podem passar para representações mais abstratas usando Símbolos matemáticos.

3 planilhas de divisão longa para os anos 3-6
prepare seus alunos para a divisão longa em todo o KS2 com essas planilhas de divisão longa.
problemas de Palavras de divisão ano 3
problemas de palavras no ano 3 geralmente usam a estrutura de agrupamento ou compartilhamento.
existem 40 bolos e 10 alunos. Quantos bolos cada aluno receberia?Como sabemos quantos grupos existem (10), precisamos calcular o valor por grupo, então esta é uma estrutura de compartilhamento. Espera-se que os alunos usem seus conhecimentos da tabela 4 vezes para resolver isso e obter a resposta 4.
Divisão: Raciocínio e resolução de problemas ano 3
para raciocínio e resolução de problemas, uma boa atividade que acho é combinar um problema de palavra com um cálculo. Por exemplo:
combine a palavra problemas que são resolvidos conhecendo 20 divididos por 4.
- existem 20 lápis e eles serão colocados em embalagens de 5. Quantos em cada pacote?
- havia 20 lápis e, em seguida, um aluno traz mais 4. Quantos lápis existem agora?
- existem 20 lápis e eles serão colocados em embalagens de 4. Quantos em cada pacote?
- havia 20 lápis e depois 4 desapareciam. Quantos lápis existem agora?
fazer com que os alunos escrevam suas explicações para cada pergunta é útil, pois permite ver seu pensamento. As perguntas foram selecionadas cuidadosamente para que os números em cada pergunta se relacionem com os números da pergunta, para que os alunos confiem em suas habilidades matemáticas para deduzir a resposta correta.
ano de Divisão 4
no Currículo Nacional de matemática na Inglaterra, para cada área de matemática delineada, existe um elemento estatutário e um elemento não estatutário. O legal elemento é da seguinte maneira:
- Lembro de multiplicação e de divisão de fatos para tabelas de multiplicação até 12 × 12
- Usar o valor de lugar, conhecido e derivados fatos para multiplicar e dividir mentalmente, incluindo: multiplicar por 0 e 1; dividindo por 1; multiplicando-se em conjunto de três números
Não-estatutárias e notas de orientação:
- os alunos continuam a praticar a recordação e o uso de tabelas de multiplicação e fatos de divisão relacionados para ajudar na fluência. Os alunos praticam métodos mentais e estendem isso a números de três dígitos para derivar fatos (por exemplo, 600 ÷ 3 = 200 pode ser derivado de 2 x 3 = 6).
- os alunos praticam para se tornarem fluentes no método formal escrito de multiplicação curta e divisão curta com respostas exatas
- os alunos resolvem problemas de duas etapas em contextos, escolhendo a operação apropriada, trabalhando com números cada vez mais difíceis. Isso deve incluir perguntas por correspondência, como o número de opções de uma refeição em um cardápio, ou três bolos compartilhados igualmente entre 10 crianças.
idéias de lição de divisão ano 4
para esta lição, vou ver como você pode começar a ensinar divisão curta usando manipulativos ao lado dela.
digamos que vamos ensinar aos alunos uma divisão curta para a questão 168 dividida por 12.
normalmente escreveríamos isso no que é comumente referido como ponto de ônibus. Mas o interessante é que diferentes lugares do mundo o escrevem de maneira diferente.
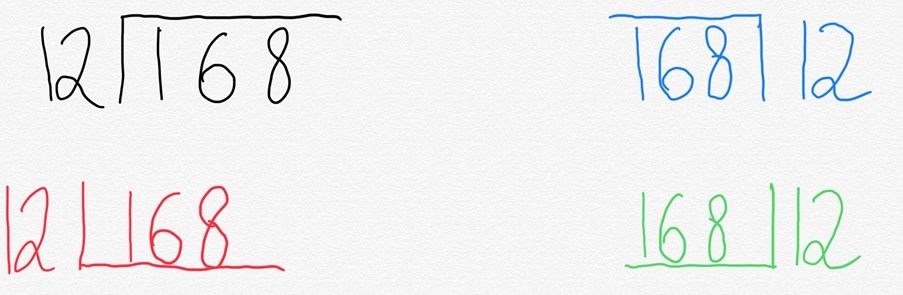
a razão para isso é bastante simples. O que o’ ponto de ônibus ‘ realmente representa é uma maneira abreviada de representar um retângulo.
quando ensinamos a divisão curta formal, o que estamos efetivamente dizendo é que você precisa imaginar um retângulo onde a largura é 12. A área total do retângulo é 168 e estamos tentando encontrar o comprimento que falta no topo. Então, como mostramos isso usando manipulativos? Blocos de Dienes são uma ferramenta útil para isso.
sabemos que o valor total é 168. Portanto, precisamos coletar 168 dienos usando as menores quantidades de blocos possíveis. Isso é mostrado abaixo.
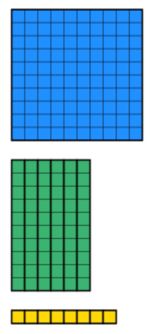
olhando para trás, sabemos que a largura é 12. Isso significa que agora precisamos manipular os blocos para obter uma largura de 12. Observe que o retângulo precisa ser sólido e não pode ter partes ausentes. Por exemplo, o abaixo não seria permitido, apesar de haver 12 unidades descendo a largura.
em vez disso, os alunos podem girar dois blocos 10s para obter o seguinte. Observe como há 12 em cada coluna e é um objeto sólido.
a parte final que os alunos devem fazer é usar os blocos restantes para criar um retângulo vendido, mantendo a largura 12. Isso pode levar algum tempo, mas com a prática, os alunos ficam mais rápidos. Depois de algum tempo, os alunos produzirão isso:
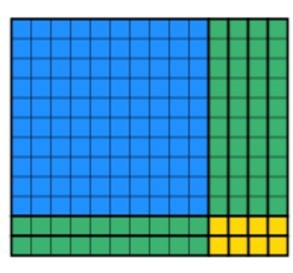
podemos ver que todos os 168 blocos foram usados e que a largura ainda é 12. Para encontrar a resposta, os alunos são obrigados a contar o comprimento, que neste caso é 14. Eu sobrepus os dois métodos abaixo para que você possa ver como eles se complementam abaixo.
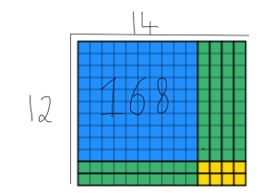
esta é uma estratégia útil para ensinar os alunos no ano 4, pois há repercussões maciças em outras áreas do currículo que já estão iluminadas para os alunos. Embora ainda não possam reconhecê – lo, ensinando divisões curtas como essa, eles já foram introduzidos no perímetro e na área-pense em quanto tempo de ensino pode ser salvo quando essa conexão é feita. Não só isso, mas em secundário, essa abordagem se transfere para o pensamento algébrico.
problemas de Palavras de divisão ano 4
espera-se que os alunos se baseiem em seu conhecimento de valor local para resolver problemas baseados em divisão e, portanto, um problema de palavra apropriado seria.
um pomar cultivou 4.800 maçãs em uma estação. Eles são colocados em embalagens de 4 antes de ir ao mercado. Quantos pacotes existem?
aqui os alunos devem usar o fato de que 4 x 12 = 48 e como 4.800 é cem vezes mais do que 48, 12 também deve por multiplicado por 100 para obter 1.200
Divisão: Raciocínio e resolução de problemas ano 4
é sempre, às vezes ou nunca verdade que a soma de três números pares é divisível por 4?
esta questão dá aos alunos ampla oportunidade de experimentar dentro dos parâmetros da questão. Os alunos que precisam de mais apoio podem olhar para números pares de dígitos e os alunos podem ir até o que eles se sentem confortáveis com.
com perguntas abertas como essa, é bom fornecer um requisito mínimo para quantas tentativas os alunos devem fazer, caso contrário, eles geralmente optarão por fazer o mínimo.
a resposta a esta pergunta é às vezes.
um “truque” rápido para saber se um número é divisível é olhar para os últimos 2 dígitos do número e ver se esses são divisíveis por 4. Por exemplo, se uma criança encontrou a soma de 34, 36 e 38 e obteve 108, como professor, sei que esse número é divisível por 4, pois os dois dígitos finais (08) fazem 8 e são divisíveis por 4. Se uma criança escolheu 34, 36 e 48 para obter 118, eu sei que isso não é divisível por 4 Como 18 – Os dois dígitos finais de 118 – não são divisíveis por 4.
ano de divisão 5
no Currículo Nacional de matemática na Inglaterra, para cada área de matemática delineada, existe um elemento estatutário e um elemento não estatutário. O elemento estatutário é o seguinte:
- Multiplicar e dividir números mentalmente baseando-se em fatos conhecidos
- Dividir números com até 4 algarismos por um número de um dígito, usando a escrita formal, o método de curto divisão e interpretar os resíduos de forma adequada para o contexto
- Multiplicar e dividir números inteiros e as que envolvem números decimais por 10, 100 e 1000
- Resolver problemas envolvendo a multiplicação e a divisão, incluindo o uso de seu conhecimento de fatores e múltiplos, quadrados e cubos
- Resolver problemas envolvendo adição, subtração, multiplicação e divisão e a combinação de estes, incluindo a compreensão do significado do sinal de igual
- resolver problemas envolvendo multiplicação e divisão, incluindo dimensionamento por frações simples e problemas envolvendo taxas simples.
Não-estatutárias e notas de orientação:
- os Alunos interpretam inteiro não respostas a divisão por expressar os resultados em diferentes maneiras, de acordo com o contexto, inclusive com restos, como frações, decimais ou por arredondamento (por exemplo, 98 ÷ 4 = = 24 r 2 = 24 = 24.5 ≈ 25).Os alunos usam multiplicação e divisão como inversos para apoiar a introdução da razão no ano 6, por exemplo, multiplicando e dividindo por potências de 10 em desenhos em escala ou multiplicando e dividindo por potências de 1.000 na conversão entre unidades como quilômetros e metros.
atividades de divisão o ano 5
divisão no ano 5 progride através do uso de restos em Respostas. Para esta lição, vou olhar para outro uso manipulativos que os professores podem usar para ensinar divisão de 4 por 1 dígitos.
se a questão fosse 5.642 dividida por 4, poderíamos representar isso usando um gráfico de valor de lugar e contadores de valor de lugar, como podemos ver abaixo.
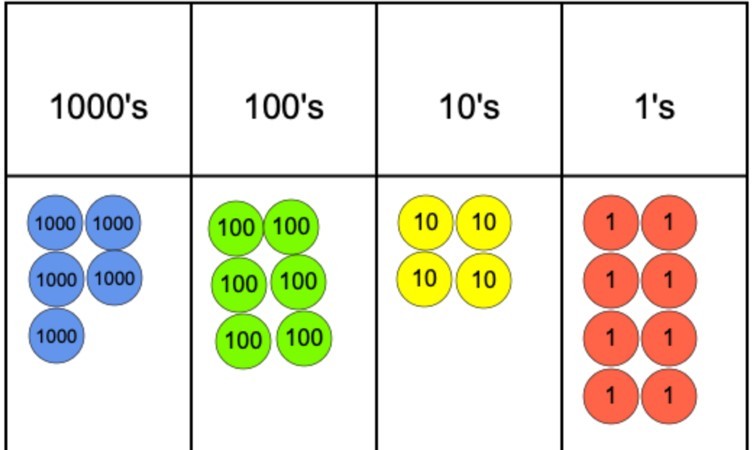
o próximo passo seria começar a agrupar os contadores em 4, pois este é o nosso divisor. No entanto, como pode ser visto, rapidamente chegamos a um problema na coluna dos anos 1000, pois somos capazes de agrupar 4 dos contadores, mas não podemos agrupar o contador restante em um grupo de 4.
para combater esse problema, o contador 1000 que não foi agrupado pode ser trocado por dez contadores 100. Estes podem então ser agrupados em grupos de 4 e isso pode acontecer sem que haja mais de 100 contadores. A partir daí, é um caso simples de passar para os anos 10 e, finalmente, para aqueles.
como existem nove contadores 1s, podemos agrupar 8 deles em 2 grupos e 4 e afirmar que resta um*. Para encontrar a resposta, tudo o que é necessário é contar o número de grupos feitos em cada valor de lugar e usá-los para escrever os dígitos para criar a resposta final. Nesse caso, a resposta seria 1.412 restante 1.
* quando você está olhando para decimais, você pode trocar o contador 1s restante por dez contadores 0.1 e continuar a divisão conforme descrito acima. Os alunos que estão familiarizados com este modelo é útil, pois pode ajudar a desmistificar a divisão com decimais com os quais os alunos podem lutar. Isso os ajuda a ver que é uma continuação de um processo com o qual eles já estão familiarizados, em vez de algo novo.
problemas de divisão ano 5
ao dividir no ano 5, Os alunos se depararão com cenários em que precisarão arredondar sua resposta para que a resposta faça sentido no contexto. Uma pergunta apropriada que demonstra isso seria algo como o seguinte:
uma escola está planejando uma discoteca distanciada social onde eles planejam oferecer 250ml de suco a cada aluno. Eles podem comprar garrafas de suco de 2 litros. Eles esperam que 33 alunos cheguem, então saiba que distribuirão 8,25 litros de suco. Quantas garrafas de suco eles precisarão comprar?
uma resposta comum é que os alunos dirão 4 e um quarto. No entanto, como você não pode comprar um quarto de garrafa, neste caso, a resposta correta seria 5 garrafas de suco seriam necessárias para garantir que todos os alunos pudessem participar.
Divisão: Raciocínio e Resolução de problemas, Ano 5
Como observado acima, no Ano 5, os alunos vão encontrar cenários dentro da divisão, onde eles terão de escolher se uma resposta precisa ser arredondados para cima ou para baixo. Por exemplo, quando uma pergunta pede aos alunos para descobrir quantos ônibus são necessários para uma escola uma viagem. Fazer com que os alunos criem seus próprios problemas usando uma variedade de contexto fornecido pode ser uma atividade realmente desafiadora que faz com que os alunos pensem matematicamente sobre contexto e divisão.
os alunos podem trocar essas perguntas que criaram com um parceiro e depois resolvê-las e verificar com o criador da pergunta original se eles têm a resposta correta.
ano de divisão 6
no Currículo Nacional de matemática na Inglaterra, para cada área de matemática delineada, existe um elemento estatutário e um elemento não estatutário. O elemento estatutário é o seguinte:
- dividir números com até 4 algarismos por um de dois dígitos número inteiro usando a escrita formal, o método de divisão longa, e interpretar os restos como número inteiro restos, frações, ou por arredondamento, conforme apropriado para o contexto
- dividir números com até 4 algarismos por um número de dois dígitos, utilizando a escrita formal, o método de curto divisão, onde apropriado, a interpretação de restos de acordo com o contexto
- executar cálculos mentais, inclusive com uma mistura de operações e números grandes
- identificar fatores comuns, comuns e múltiplos de números primos
- use os seus conhecimentos de ordem de operações para realizar cálculos envolvendo as quatro operações
Não-estatutárias e notas de orientação:
- Resolver problemas envolvendo adição, subtração, multiplicação e divisão
- Use estimativa para verificar as respostas para cálculos e determinar, no contexto de um problema, um grau adequado de rigor.
idéias de lição de divisão ano 6
Sophie Bartlett (@_MissieBee) criou um excelente blog aqui (link para o blog de Sophie sobre ensino de longa divisão) detalhando como ela ensinaria longa divisão por um ano 6 classe. Como a divisão longa é o único novo aprendizado sobre a divisão para o ano 6, esta é uma maneira ideal de introduzir o procedimento de divisão longa.
perguntas da Divisão ano 6
um problema típico de palavras de divisão que um aluno do ano 6 encontraria seria:
uma escola levantou £3.146 de uma venda de bolos. 104 pais participaram do evento. Se todos os pais gastaram uma quantia igual de dinheiro, quanto cada pai gastou?
aqui, espera-se que os alunos usem o método de divisão longa para resolver esta questão para obter a resposta £30,25.
Divisão: raciocínio e resolução de problemas ano 6
com algo processual como divisão longa, uma boa atividade de raciocínio é fazer com que os alunos encontrem erros. Esses recursos fornecem um grande banco de tais atividades. Como podemos ver na pergunta abaixo, os alunos fizeram todo o trabalho duro, mas um erro descuidado na contagem dos grupos de 59 significa que a criança acreditava que 59 x 7 era 472 e não 59 x 8.
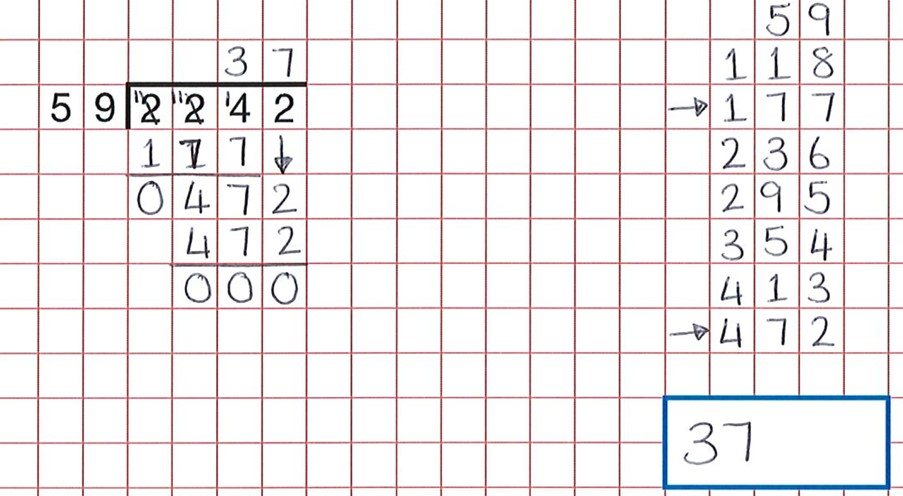
a resposta correta teria sido 38.
a divisão é um tópico chave da matemática, não apenas no KS2, mas na matemática como um todo. Espero que este post tenha lhe dado algumas boas ideias para ajudar seus alunos a abordá-lo com confiança.
aulas de matemática Online de 1 a 1 com a confiança de escolas e professores
todas as semanas, os tutores especializados em matemática da Third Space Learning apoiam milhares de crianças do ensino fundamental com aulas semanais on-line de 1 a 1 e intervenções matemáticas. Desde 2013, ajudamos mais de 100.000 crianças a se tornarem matemáticos mais confiantes e capazes. Saiba mais ou solicite um orçamento personalizado para falar conosco sobre suas necessidades e como podemos ajudar.
ensino primário voltado para as necessidades de cada criança e seguindo de perto o Currículo Nacional.