vârfurile, fețele și marginile apar foarte mult în geometria școlii primare atunci când copiii învață despre proprietățile formelor 3d. Aici vă explicăm ce înseamnă fiecare dintre acestea și cum să calculați numărul de vârfuri, fețe și margini pentru orice formă. De asemenea, includem numărul de margini, fețe și vârfuri ale celor mai comune forme.
acest vocabular este introdus în curriculumul național la anul 2, astfel încât următoarele informații pot fi utilizate cu elevii de-a lungul anilor de școală primară. Chiar și elevii din anul 1 pot începe să se angajeze cu proprietăți De forme în acest fel dacă doriți să le dați un început!
ce sunt vârfurile în forme?
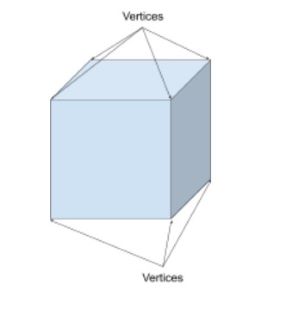
nodurile în forme sunt punctele în care se întâlnesc două sau mai multe segmente de linie sau muchii (ca un colț). Singularul vârfurilor este vertex. De exemplu, un cub are 8 vârfuri și un con are un vârf.
nodurile sunt uneori numite colțuri, dar atunci când se ocupă cu forme 2D și 3D, cuvântul noduri este preferat.
un cub are 8 vârfuri. 7 sunt vizibile aici și unul este ascuns.
ce sunt marginile?
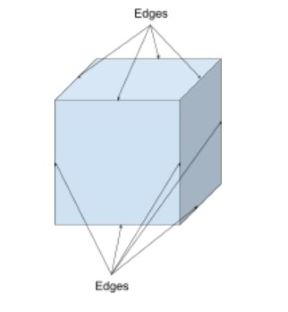
marginile sunt segmentele de linie care unesc un nod cu altul și sunt, de asemenea, locul în care se întâlnesc fețele formei. Acestea pot fi folosite pentru a descrie formele 2d și 3D.
deși multe forme au linii drepte și muchii drepte, există forme care au muchii curbate, cum ar fi o emisferă. Un cub va avea 12 margini drepte așa cum se vede mai jos; 9 sunt vizibile și 3 sunt ascunse.

forme 3D gratuite foi de lucru independente de recapitulare
Ajutați elevii din anul 2 (și mai în vârstă) să revizuiască vârfurile, fețele și marginile cu foile noastre de lucru gratuite independente de recapitulare.
ce sunt fețele?
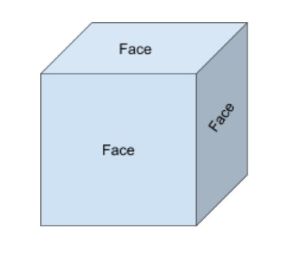
fețele sunt suprafața plană a unei forme solide. De exemplu, un cuboid are 6 fețe. Când ne gândim la formele 2d și 3D, este important să știm că o formă 2D reprezintă doar fața unei forme 3D.
de asemenea, este important să știm că, deoarece realitatea noastră este construită în 3 dimensiuni, este imposibil să gestionăm fizic formele 2D, deoarece suntem înconjurați de forme 3-dimensionale. Prin urmare, dacă în clasă există un sertar etichetat ‘forme 2d’, acest lucru ar trebui eliminat, deoarece îi învață pe copii o concepție greșită. Deși un concept interactiv pentru clasă, formele 2d pot exista doar ca desene dimensionale 2.
puteți avea atât fețe plate, cât și fețe curbate, dar mi se pare util să mă refer la fețele curbate ca suprafețe curbate, deoarece se potrivește bine cu aspectul vizual al formei.
există trei fețe care sunt vizibile și trei care sunt ascunse pe cubul de mai jos.
vârfuri, fețe și muchii de forme 3D comune
câte fețe, muchii și vârfuri are un cuboid?
un cuboid are 8 vârfuri.
un cuboid are 12 muchii.
un cuboid are 6 fețe.

câte fețe, muchii și vârfuri are un cilindru?
un cilindru are 0 vârfuri.
un cilindru are 2 muchii.
un cilindru are 2 fețe și 1 suprafață curbată.

câte fețe, muchii și vârfuri are o emisferă?
o emisferă are 0 vârfuri.
o emisferă are 1 margine curbată.
o emisferă are 1 față și 1 suprafață curbată.

câte fețe, muchii și vârfuri are un con?
un con are 1 vârf.
un con are 1 margine.
o emisferă are 1 față și 1 suprafață curbată.

câte fețe, muchii și vârfuri are un tetraedru?
un tetraedru are 4 vârfuri.
un tetraedru are 6 muchii.
un tetraedru are 4 fețe.

câte fețe, muchii și vârfuri are o sferă?
o sferă are 0 vârfuri.
un tetraedru are 0 muchii.
un tetraedru are 1 suprafață curbată.

câte fețe, muchii și vârfuri are o prismă?
o prismă este un obiect solid, formă geometrică sau poliedru în care fețele ambelor capete au aceeași formă. Ca atare, elevii vor întâlni multe tipuri de prisme pe tot parcursul școlarizării. Cele obișnuite includ cuburi, cuboide, prisme triunghiulare, prisme pentagonale și prisme hexagonale.
| formă | Pictorial | fețe | muchii | vârfuri |
|---|---|---|---|---|
| prisma triunghiulară | 5 | 9 | 6 | |
| prisma pentagonală | 7 | 15 | 10 | |
| prismă hexagonală | 8 | 18 | 12 | |
| cub |  |
6 | 8 | 12 |
| Cuboid |
 |
6 | 8 | 12 |
când învață copiii despre vârfuri, fețe și margini în școala primară?
copiii trebuie să fie introduși în mod oficial în vocabularul vârfurilor, fețelor și marginilor în anul 2 atunci când studiază geometria. Cu toate acestea, profesorii pot face alegerea de a introduce acest vocabular mai devreme.
anul 2 elevii ar trebui să poată:
- identificarea și descrierea proprietăților formelor 3-D, inclusiv numărul de muchii, vârfuri și fețe
ghidul non-statutar prevede că:
- elevii manipulează și numesc o mare varietate de forme comune 2-d și 3-d, inclusiv: patrulatere și poligoane și cuboide, prisme și conuri și identifică proprietățile fiecărei forme (de exemplu, numărul de laturi, numărul de fețe). Elevii identifică, compară și sortează formele pe baza proprietăților lor și folosesc vocabularul cu precizie, cum ar fi laturile, marginile, vârfurile și fețele.
din acest moment, curriculum-ul național nu face referire la vârfuri, fețe și margini în mod explicit din nou, astfel încât profesorii din alte grupuri de ani vor trebui să continue să folosească acest vocabular atunci când se uită la forma
cum se raportează vârfurile, fețele și marginile la alte domenii ale matematicii?
elevii vor folosi cunoștințele de noduri, fețe și margini atunci când se uită la forme 2d, precum și forme 3d. Știind ce margini sunt și identificarea lor pe forme compuse este crucială pentru găsirea perimetrului și a zonei formelor compuse 2D. Este o bază importantă pentru anii următori atunci când se ocupă de diferite teoreme matematice, cum ar fi teoria grafurilor și parabolele.
cum se raportează vârfurile, fețele și marginile la viața reală?
orice obiect din viața reală are vârfuri, fețe și muchii. De exemplu, un cristal este un octaedru – are opt fețe, douăsprezece margini și șase vârfuri. Cunoașterea acestor proprietăți pentru diferite forme tridimensionale pune bazele diferitelor industrii, cum ar fi arhitectura, designul interior, ingineria și multe altele.
noduri, fețe și muchii Exemple de întrebări
1. Explicați ce este un vârf.
(răspuns: un nod este locul unde se întâlnesc două linii)
2. Câte margini are o prismă triunghiulară?
(răspuns: 9)
3. Câte vârfuri are un con?
(răspuns: 1 vârf)
4. Câte fețe are un cuboid? Care sunt formele 2D ale acestor fețe?
(răspuns: 6 fețe. Pot avea 2 fețe pătrate și 4 fețe dreptunghiulare sau doar 6 fețe dreptunghiulare.)
5. Pentru toate prismele comune (cuburi, cuboide, prisme triunghiulare, prisme pentagonale și prisme hexagonale) adăugați fețele și vârfurile împreună și scădeți marginile. Ce observați despre răspunsuri?
(Răspuns: Răspunsul este întotdeauna 2. Aceasta este cunoscută sub numele de formula lui Euler (număr de vârfuri – număr de margini + număr de fețe = 2)
vă întrebați cum să explicați copiilor dvs. alte vocabular cheie de matematică? Consultați dicționarul nostru de matematică primară sau încercați aceste:
- ce este Maths Mastery?
- ce sunt formele 2d?
- ce sunt formele 3d?
puteți găsi o mulțime de planuri de lecții de geometrie și foi de lucru imprimabile pentru elevii de școală primară pe al treilea spațiu de învățare matematică Hub.
lecții de matematică Online 1-la-1 de încredere de către școli și profesori
în fiecare săptămână, tutorii specializați în matematică ai Third Space Learning susțin mii de copii din școala primară cu lecții săptămânale online 1-la-1 și intervenții matematice. Din 2013 am ajutat peste 100.000 de copii să devină matematicieni mai încrezători și mai capabili. Aflați mai multe sau solicitați o ofertă personalizată pentru a ne vorbi despre nevoile dvs. și despre modul în care vă putem ajuta.
școlarizarea noastră online pentru programul de Matematică oferă fiecărui copil propriul tutore profesionist unu la unu la matematică