Divizia din etapa cheie 2 formează ultima parte a celor patru operații – cele patru concepte matematice de bază pe care elevii ar trebui să le cunoască. Acest blog vă va ajuta să vă asigurați că toți elevii dvs., din anul 3 până în anul 6, pot aborda diviziunea cu încrederea de care au nevoie pentru a reuși.
diviziunea în matematica KS2 se bazează pe ceea ce a fost învățat la KS1. Până la sfârșitul Y2 elevii de la standardul așteptat va fi capabil să ‘amintesc și de a folosi multiplicare și divizare fapte pentru 2, 5 și 10 tabele de multiplicare, inclusiv recunoașterea numere impare și pare.’
pentru profesorii din anul 3, este întotdeauna o idee bună să ne asigurăm că elevii le cunosc foarte bine. Prin aceasta, nu mă refer pur și simplu la faptul că pot papagaliza faptele divizării la tine, ci înțeleg cu adevărat cum să reprezinte aceste fapte atât cu reprezentări concrete, explicații verbale, cât și prin alte metode picturale.
elevii care nu sunt capabili să facă acest lucru, dar sunt capabili să vă spună verbal faptele diviziunii, au o înțelegere foarte superficială a diviziunii și pentru ca aceștia să progreseze în activități mai dificile de rezolvare a problemelor, aprofundarea înțelegerii conceptuale a diviziunii este o necesitate la Anul 3.
curriculumul național plasează diviziunea în aceeași secțiune ca înmulțirea pentru anii 3-5 și o plasează într-o secțiune numită ‘patru operații’ în anul 6. Părțile preluate din programa națională se referă numai la cele care menționează în mod specific diviziunea. Celelalte elemente ale acestor secțiuni pot fi găsite în blogul despre înmulțire sau adunare și scădere, după caz.
Ce Este Diviziunea?
diviziunea este una dintre cele patru operații – cele patru concepte matematice de bază pe care elevii ar trebui să le cunoască – alături de adunare, scădere și înmulțire.
unde înmulțirea combină un număr de mai multe ori, împărțirea este opusul: de câte ori un număr este conținut în altul. De exemplu, împărțirea 10 la 2 se întreabă de câte ori 2 este conținut în 10.

din intervențiile matematice online ale Third Space Learning.
Divizia de predare KS2-teoria
diviziunea este inversul înmulțirii. Ca și în cazul blogului de multiplicare, predarea diviziunii conține trei structuri subiacente, care, atunci când sunt cuplate cu fapte de divizare și înțelegere conceptuală, vor oferi studenților cea mai bună oportunitate de a avea succes atunci când rezolvă probleme legate de diviziune.
cele trei structuri sunt partajarea, gruparea și scalarea. Deși nu este suficient timp pentru a le explora în profunzime, ceea ce urmează va fi doar o scurtă introducere a acestora.
partajarea și gruparea sunt inversul înmulțirii ca adunare repetată. Partajarea este un concept structural care este introdus în KS1 și mai devreme în cazul în care, după cum sugerează și numele, o sumă este împărțită în grupuri egale.
de exemplu, 12 mere sunt împărțite între 3 elevi. Câte mere primește fiecare elev? Aici știm întreaga cantitate (12 mere) și, în mod crucial, știm în ce cantitate vom împărți (3). În funcție de locul în care se află elevii în călătoria lor matematică, aceștia pot scădea în mod repetat cu un anumit număr (1, 2, 3 sau 4) din cantitate în trei grămezi care reprezintă cei trei elevi.
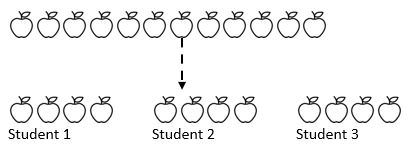
după cum putem vedea din cele de mai sus, întreaga sumă a fost împărțită în trei grupuri egale.
gruparea este similară cu partajarea, dar ceea ce știm este ușor diferit în comparație cu partajarea. În structura de partajare, știm cantitatea de grupuri pe care partajarea va avea loc. În structura de grupare, știm suma din fiecare grup, dar nu Numărul de grupuri reale care există.
de exemplu, 12 mere sunt împărțite în grupuri de 4. Câte grupuri vor fi? Deși această întrebare este foarte asemănătoare cu cea de mai sus, acum preia structura de grupare, deoarece știm câți vor intra în fiecare grup, dar nu mai știm câte grupuri vor exista acum.
după cum știm că există 4 în fiecare grup, putem grupa 4 mere până când am acoperit toate cele 12 pentru a vedea că există 3 grupuri.
structura finală a diviziunii este scalarea. În timp ce în multiplicare creșteam o valoare, structura diviziunii scade. De exemplu, Shannen are 6 pixuri, iar Jen are de 3 ori mai puține. Câte pixuri are Jen?
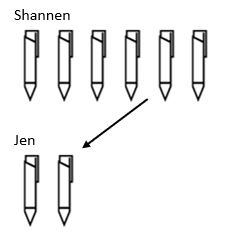
aici putem vedea că pentru a găsi cantitatea totală de pixuri pe care le are Jen, a trebuit să luăm cantitatea pe care o avea Shannen și să o micșorăm cu un factor de scară de 3, astfel încât Jen să ajungă cu 2 pixuri.
din experiență, aceasta este cea mai grea structură de diviziune pe care elevii o pot înțelege și înțelege și este una care trebuie revizuită împreună cu scalarea ca multiplicare, deoarece aceasta este o abilitate crucială atunci când convertiți măsurătorile și monedele dintr-o cantitate mai mare într-o cantitate mai mică. De exemplu, kilometri până la mile.
Divizia Anul 3
în curriculumul național de Matematică din Anglia, pentru fiecare domeniu de matematică prezentat, există atât un element statutar, cât și un element non-statutar. Elementul statutar este următorul:
- rechemare și de a folosi multiplicare și divizare fapte pentru 3, 4 și 8 tabele de multiplicare
- scrie și calcula declarații matematice pentru înmulțire și împărțire folosind tabelele de multiplicare pe care le cunosc, inclusiv pentru numere de două cifre ori numere de o cifră, folosind mentale și progresează la metode formale scrise
- rezolva probleme, inclusiv probleme de numere lipsă, care implică înmulțire și împărțire, inclusiv probleme de scalare întreg pozitiv și probleme de corespondență în care n obiecte sunt conectate la M obiecte.
note și îndrumări nestatutare:
- elevii dezvoltă metode mentale eficiente, de exemplu, folosind comutativitatea și asociativitatea (de exemplu, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) și fapte de înmulțire și împărțire (de exemplu, folosind 3 × 2 = 6, 6 ÷ 3 = 2 și 2 = 6 3) pentru a obține fapte conexe (de exemplu, 30 × 2 = 60, 60 ÷ 3 = 20 și 20 = 60 int 3).
- elevii dezvoltă metode scrise fiabile pentru înmulțire și împărțire, începând cu calculele numerelor din două cifre cu numere dintr-o singură cifră și progresând la metodele formale scrise de înmulțire și împărțire scurtă.
- elevii rezolvă probleme simple în contexte, hotărând care dintre cele patru operații să folosească și de ce. Acestea includ contexte de măsurare și scalare (de exemplu, de patru ori mai mari, de opt ori mai lungi etc.) și probleme de corespondență în care obiectele m sunt conectate la n obiecte (de exemplu, 3 pălării și 4 Paltoane, câte ținute diferite?; 12 dulciuri împărțite în mod egal între 4 copii; 4 prăjituri împărțite în mod egal între 8 copii).
activități de divizare Anul 3
aceasta nu va acoperi o lecție în sine, ci va oferi un ghid cu privire la modul în care diviziunea poate fi predată cu o anumită înțelegere conceptuală în această etapă. O condiție prealabilă pentru aceasta ar fi predarea faptelor de multiplicare conexe mai întâi înainte de a preda orice diviziune conexă.
când ne gândim la structuri, cel mai bine este ca în această parte a călătoriei de învățare a elevilor să rămânem la grupare și partajare. Pentru următoarele exemple, ne vom uita la curs de dezvoltare înțelegerea elevilor de divizare de 4. Va urma abordarea concretă-picturală-abstractă.
adesea înțelegerea numărului de către studenți poate limita progresul lor în diviziune. Mai ales atunci când vine vorba de gruparea și partajarea atunci când acestea iau doar unul departe continuu de întreg.
de la începutul diviziei de predare, profesorii ar trebui să se bazeze pe ceea ce elevii știu deja despre numere pare și alte fapte de număr pentru a progresa elevii pe numărarea în orice număr ar fi adecvat.
contoarele pot fi folosite pentru a demonstra fapte legate de diviziune, deoarece elevii vor fi folosit teze atunci când își construiesc înțelegerea conceptuală a multiplicării. Întrebări precum: ‘câte grupuri de 4 sunt acolo? și câți sunt în fiecare grup? ar trebui să fie întrebat și răspunsurile ar trebui să se refere la modul în care aceasta arată diviziunea.
Învățătorul: câte contoare există?
Copil: Patru
Profesor: Bun. Acesta este un grup de patru. Câte grupuri de patru sunt acolo?
Copil: Unul
Profesor: Excelent. Avem patru contoare într-un singur grup. Am grupat patru contoare într-un singur grup. Ce am făcut?
copil: grupate patru contoare într-un singur grup.
Profesor: Genial. Când grupăm patru contoare într-un singur grup, am făcut calculul matematic al patru împărțit la unul. Ce calcul am făcut?
copil: patru împărțit la unul.
Învățătorul: și când rezolvăm patru împărțit la unu răspunsul este patru pentru că am făcut un grup care are patru elemente în el. Patru împărțit la unu este de patru. Ce este patru împărțit la unul?
copil: Patru împărțit la unu este de patru.
profesor: excelent
puteți vedea cum s-ar repeta acest lucru pentru următoarele:
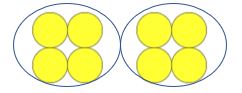
Învățătorul: câte contoare există?
copil: opt
Profesor: bine, acesta este un grup de patru. Câte grupuri de patru sunt acolo?
Copil: Doi
Profesor: Excelent. Avem patru contoare într-un singur grup. Am grupat patru contoare în două grupuri. Ce am făcut?
copil: grupate patru contoare în două grupuri.
Profesor: Genial. Când grupăm patru contoare în două grupuri, am făcut calculul matematic al opt împărțit la două. Ce calcul am făcut?
copil: opt împărțit la doi.
Învățătorul: și când rezolvăm opt împărțit la doi răspunsul este patru pentru că am făcut două grupuri care au patru elemente în el. Opt împărțit la doi este de patru. Ce este opt împărțit la două?
copil: opt împărțit la doi este de patru.
profesor: excelent
când elevii încep să devină încrezători în acest lucru, putem trece la alte modele, cum ar fi tijele Cuisenaire.

aici întreaga sumă este reprezentată în trenul de sus și tija purpurie (care în acest caz reprezintă 4 și dacă ați citit alte bloguri din această serie sperăm că veți ști cât de mult sunt un avocat pentru utilizarea lor în clasă și astfel elevii vor fi conștienți de valoarea sa până atunci) este folosit pentru a arăta câte grupuri de 4 pot intra în suma totală.
elevii pot trece apoi la elaborarea scenariilor citite de profesor. De exemplu. Există 24 de butoane și trebuie grupate în 4. Câte grupuri sunt acolo? Elevii ar putea desena aceste butoane și să le grupeze în 4 etc.
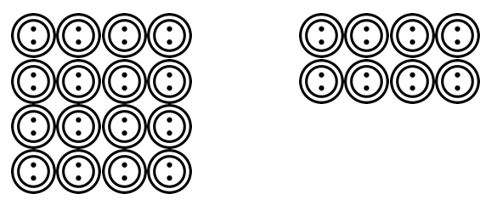
odată ce elevii s-au obișnuit să poată vizualiza aceste scenarii de grupare sau partajare a diviziunilor într-o serie de contexte, atunci pot trece la reprezentări mai abstracte folosind simboluri matematice.

3 foi de lucru cu diviziune lungă pentru anii 3-6
pregătiți-vă elevii pentru diviziune lungă în KS2 cu aceste foi de lucru cu diviziune lungă.
Probleme Word Division Anul 3
problemele Word din anul 3 vor folosi în mod obișnuit structura de grupare sau partajare.
sunt 40 de prăjituri și 10 elevi. Câte prăjituri ar primi fiecare elev?
după cum știm cât de multe grupuri sunt (10) avem nevoie pentru a lucra în suma pe grup, astfel încât aceasta este o structură de partajare. Elevii ar fi de așteptat să-și folosească cunoștințele despre tabelul de 4 ori pentru a rezolva acest lucru și pentru a obține răspunsul 4.
diviziune: Raționament și rezolvarea problemelor Anul 3
pentru raționament și rezolvarea problemelor, o activitate bună pe care o găsesc este să potrivesc o problemă de cuvânt cu un calcul. De exemplu:
potriviți problemele de cuvinte care sunt rezolvate prin cunoașterea 20 împărțit la 4.
- sunt 20 de creioane și vor fi puse în pachete de 5. Câte în fiecare pachet?
- erau 20 de creioane și apoi un student aduce încă 4. Câte creioane sunt acum?
- există 20 de creioane și vor fi plasate în pachete de 4. Câte în fiecare pachet?
- au fost 20 de creioane și apoi 4 dispar. Câte creioane sunt acum?
obținerea elevilor să-și scrie explicațiile pentru fiecare întrebare este utilă, deoarece le permite să le vadă gândirea. Întrebările au fost selectate cu atenție, astfel încât numerele din fiecare întrebare se referă la numerele de pe întrebarea astfel încât elevii se bazează pe abilitățile lor matematice pentru a deduce răspunsul corect.
Divizia Anul 4
în curriculumul național de Matematică din Anglia, pentru fiecare domeniu de matematică prezentat, există atât un element statutar, cât și un element non-statutar. Elementul statutar este următorul:
- rechemare înmulțire și împărțire fapte pentru tabele de multiplicare până la 12 octombrie 12
- folosiți valoarea locului, fapte cunoscute și derivate pentru a înmulți și împărți mental, inclusiv: înmulțirea cu 0 și 1; împărțirea cu 1; înmulțirea împreună trei numere
note și îndrumări nestatutare:
- elevii continuă să practice rechemarea și utilizarea tabelelor de înmulțire și a faptelor legate de diviziune pentru a ajuta fluența.
- elevii practică metode mentale și extind acest lucru la numere de trei cifre pentru a obține fapte (de exemplu, 600 3 = 200 pot fi derivate din 2 x 3 = 6).
- elevii exersează pentru a deveni fluenți în metoda formală scrisă de înmulțire scurtă și împărțire scurtă cu răspunsuri exacte
- elevii rezolvă probleme în doi pași în contexte, alegând operația corespunzătoare, lucrând cu numere din ce în ce mai grele. Aceasta ar trebui să includă întrebări de corespondență, cum ar fi numărul de alegeri ale unei mese dintr-un meniu sau trei prăjituri împărțite în mod egal între 10 copii.
idei de lecții de diviziune Anul 4
pentru această lecție, mă voi uita la modul în care puteți începe să predați diviziunea scurtă folosind manipulative alături de ea.
să spunem că vom învăța elevii diviziune scurtă pentru întrebarea 168 împărțit la 12.
în mod normal, am scrie acest lucru în ceea ce este denumit în mod obișnuit stația de autobuz. Dar ceea ce este interesant este că diferite locuri din lume o scriu diferit.
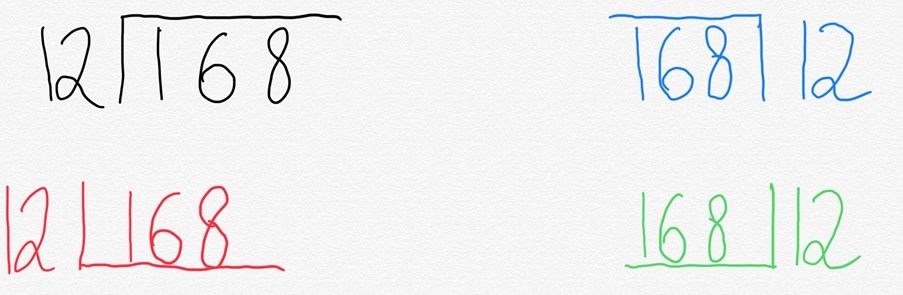
motivul pentru aceasta este destul de simplu. Ceea ce reprezintă de fapt stația de autobuz este un mod scurtat de a reprezenta un dreptunghi.
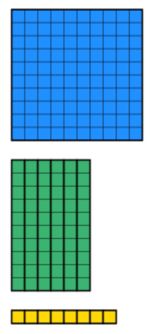
când predăm diviziunea formală scurtă, ceea ce spunem efectiv este că trebuie să vă imaginați un dreptunghi unde lățimea este 12. Suprafața totală a dreptunghiului este 168 și încercăm să găsim lungimea lipsă în partea de sus. Deci, cum putem arăta acest lucru folosind manipulative? Blocurile Dienes sunt un instrument util pentru acest lucru.
știm că suma totală este de 168. Deci, avem nevoie pentru a aduna 168 în valoare de dienes folosind cele mai mici cantități de blocuri posibile. Acest lucru este prezentat mai jos.
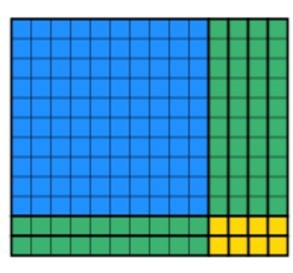
Privind înapoi la întrebare, știm că lățimea este 12. Asta înseamnă că acum trebuie să manipulăm blocurile astfel încât să obținem o lățime de 12. Rețineți că dreptunghiul trebuie să fie solid și nu poate avea părți lipsă. De exemplu, cele de mai jos nu ar fi permise, în ciuda faptului că există 12 unități care coboară pe lățime.
în schimb, elevii pot roti două blocuri 10s pentru a obține următoarele. Observați cum există 12 în fiecare coloană și este un obiect solid.
partea finală pe care elevii trebuie să o facă este să folosească blocurile rămase pentru a crea un dreptunghi vândut, păstrând în același timp lățimea 12. Acest lucru ar putea dura ceva timp, dar cu practica, elevii obține mai repede. După ceva timp, elevii vor produce acest lucru:
putem vedea că toate blocurile 168 au fost folosite și că lățimea este încă 12. Pentru a găsi răspunsul, elevii trebuie să numere lungimea, care în acest caz este de 14. Am suprapus ambele metode de mai jos, astfel încât să puteți vedea cum se completează reciproc mai jos.
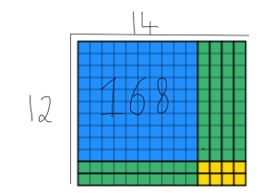
aceasta este o strategie utilă pentru a preda elevilor în anul 4, deoarece există repercusiuni masive în alte domenii ale curriculumului care sunt deja iluminate studenților.
deși s – ar putea să nu-l recunoască încă, învățând o diviziune scurtă ca aceasta, ei au fost deja introduși în perimetru și zonă-gândiți-vă cât timp de predare poate fi economisit atunci când se face această conexiune. Nu numai asta, dar în secundar, această abordare se transferă gândirii algebrice.
probleme de divizare a cuvintelor Anul 4
elevii ar fi de așteptat să se bazeze pe cunoștințele lor despre valoarea locului pentru a rezolva problemele bazate pe diviziune și astfel ar fi o problemă de cuvânt adecvată.
o livadă a cultivat 4.800 de mere într-un sezon. Acestea sunt plasate în pachete de 4 înainte de a merge pe piață. Câte pachete sunt acolo?
aici elevii ar trebui să folosească faptul că 4 x 12 = 48 și ca 4800 este de o sută de ori mai mult decât 48, 12 trebuie, de asemenea, înmulțită cu 100 pentru a obține 1200
diviziune: Raționament și rezolvarea problemelor Anul 4
este întotdeauna, uneori sau niciodată adevărat că suma a trei numere pare este divizibilă cu 4?
această întrebare oferă studenților posibilitatea de a experimenta în parametrii întrebării. Elevii care au nevoie de mai mult sprijin se pot uita la numerele sing digit chiar și elevii ar putea merge până la orice se simt confortabil cu.
cu întrebări deschise, cum ar fi acest lucru, este bine să ofere o cerință minimă pentru cât de multe încercări elevii ar trebui să facă altfel ei vor alege de multe ori să facă minimul.
răspunsul la această întrebare este uneori.
un truc rapid pentru a ști dacă un număr este divizibil este să te uiți la ultimele 2 cifre ale numărului și să vezi dacă acestea sunt divizibile cu 4. De exemplu, dacă un copil a găsit suma de 34, 36 și 38 și a obținut 108, ca profesor știu că acest număr este divizibil cu 4, deoarece ultimele două cifre (08) fac 8 și sunt divizibile cu 4. Dacă un copil a ales 34, 36 și 48 pentru a obține 118, știu că acest lucru nu este divizibil cu 4, deoarece 18 – ultimele două cifre ale lui 118 – nu sunt divizibile cu 4.
Divizia anul 5
în curriculumul național de Matematică din Anglia, pentru fiecare domeniu de matematică prezentat, există atât un element statutar, cât și un element non-statutar. Elementul statutar este următorul:
- înmulțiți și împărțiți numerele bazându-vă mental pe fapte cunoscute
- împărțiți numerele de până la 4 cifre cu un număr dintr-o singură cifră folosind metoda formală scrisă de divizare scurtă și interpretați resturile în mod corespunzător pentru context
- înmulțiți și împărțiți numerele întregi și cele care implică zecimale cu 10, 100 și 1000
- rezolvați problemele care implică înmulțirea și împărțirea, inclusiv multipli, pătrate și cuburi
- rezolva problemele care implică adunare, scădere, înmulțire și împărțire și o combinație de acestea, inclusiv înțelegerea semnificației semnului egal
- rezolvă probleme care implică înmulțirea și împărțirea, inclusiv scalarea prin fracții simple și probleme care implică rate simple.
note și îndrumări nestatutare:
- elevii interpretează răspunsurile non-întregi la împărțire prin exprimarea rezultatelor în moduri diferite în funcție de context, inclusiv cu resturi, ca fracții, ca zecimale sau prin rotunjire (de exemplu, 98 int 4 = = 24 R 2 = 24 = 24,5 int 25).
- elevii folosesc înmulțirea și împărțirea ca inverse pentru a susține introducerea raportului în anul 6, de exemplu, prin înmulțirea și împărțirea cu puteri de 10 în desenele la scară sau prin înmulțirea și împărțirea cu puteri de 1.000 în conversia între unități precum kilometri și metri.
activități de divizare anul 5
diviziunea în anul 5 progresează prin utilizarea resturilor în răspunsuri. Pentru această lecție, mă voi uita la o altă utilizare manipulative pe care profesorii le pot folosi pentru a preda diviziunea 4-cu-1-cifre.
dacă întrebarea ar fi 5.642 împărțită la 4, am putea reprezenta acest lucru folosind o diagramă a valorii locului și contoare de valoare a locului, după cum putem vedea mai jos.
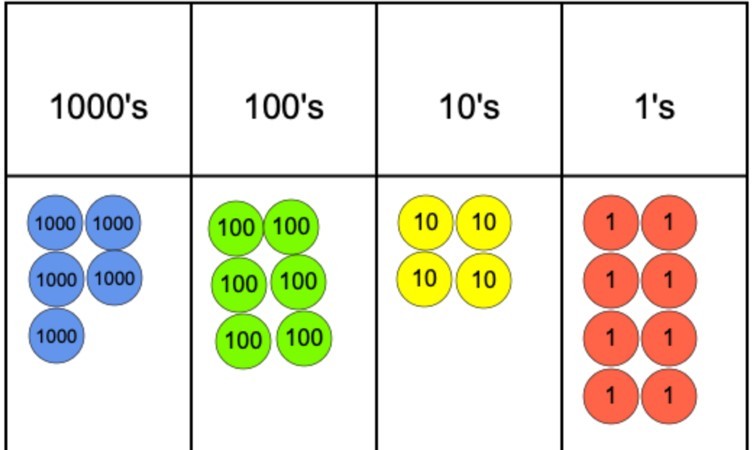
următorul pas ar fi să începem să grupăm contoarele în 4, deoarece acesta este divizorul nostru. Cu toate acestea, după cum se poate observa, ajungem rapid la o problemă în coloana 1000, deoarece suntem capabili să grupăm 4 dintre contoare, dar atunci nu putem grupa contorul rămas într-un grup de 4.
pentru a combate această problemă, contorul 1000 care nu a fost grupat poate fi schimbat pentru zece contoare 100. Acestea pot fi apoi grupate în grupuri de 4 și acest lucru se poate întâmpla fără a exista contoare 100s rămase. De acolo, este un caz simplu de a trece apoi la anii 10 și în cele din urmă la cei.
deoarece există nouă contoare 1s, putem grupa 8 dintre ele în 2 grupuri și 4 și susținem că a mai rămas unul*. Pentru a găsi răspunsul, tot ce este necesar este să numărați numărul de grupuri realizate în fiecare valoare a locului și să le folosiți pentru a scrie cifrele pentru a crea răspunsul final. În acest caz, răspunsul ar fi 1.412 rest 1.
* când vă uitați la zecimale, puteți schimba contorul 1s rămas pentru zece contoare 0.1 și continuați diviziunea așa cum este descris mai sus. Elevii care sunt familiarizați cu acest model sunt utili, deoarece pot ajuta la demistificarea diviziunii cu zecimale cu care elevii se pot lupta. Acest lucru îi ajută să vadă că este o continuare a unui proces cu care sunt deja familiarizați, mai degrabă decât ceva nou.
probleme de diviziune anul 5
când se împarte în anul 5, elevii vor întâlni scenarii în care vor trebui să-și rotunjească răspunsul pentru ca răspunsul să aibă sens în context. O întrebare adecvată care demonstrează acest lucru ar fi ceva de genul:
o școală planifică o discotecă distanțată socială în care intenționează să ofere 250 ml de suc fiecărui elev. Ei pot cumpăra sticle de suc de 2 litri. Se așteaptă ca 33 de studenți să sosească, astfel încât să știe că vor da 8,25 litri de suc. Câte sticle de suc vor trebui să cumpere?
un răspuns comun este că elevii vor spune 4 și un sfert. Cu toate acestea, deoarece nu puteți cumpăra un sfert de sticlă, în acest caz răspunsul corect ar fi 5 sticle de suc ar fi necesare pentru a se asigura că toți elevii ar putea lua parte.
Divizia: raționament și rezolvarea problemelor anul 5
după cum sa menționat mai sus, în anul 5, elevii vor întâlni scenarii în cadrul diviziei în care li se va cere să aleagă dacă un răspuns trebuie rotunjit în sus sau în jos. De exemplu, atunci când o întrebare cere elevilor să lucreze cât de multe autobuze sunt necesare pentru o școală o excursie.
a-i determina pe elevi să-și creeze propriile probleme folosind o serie de contexte furnizate poate fi o activitate cu adevărat provocatoare, care îi determină pe elevi să se gândească matematic la context și diviziune.
elevii pot apoi să schimbe aceste întrebări pe care le-au creat cu un partener și apoi să le rezolve și să verifice cu creatorul întrebării originale dacă au răspunsul corect.
Divizia Anul 6
în curriculumul național de Matematică din Anglia, pentru fiecare domeniu de matematică prezentat, există atât un element statutar, cât și un element non-statutar. Elementul statutar este următorul:
- împărțiți numerele de până la 4 cifre la un număr întreg din două cifre folosind metoda formală scrisă de divizare lungă și interpretați resturile ca resturi de numere întregi, fracții sau prin rotunjire, după caz pentru contextul
- împărțiți numerele de până la 4 cifre la un număr din două cifre folosind metoda formală scrisă de divizare scurtă, după caz, interpretarea resturilor în funcție de context
- efectuați calcule mentale, inclusiv numerele
- identifică factori comuni, multipli comuni și numere prime
- să utilizeze cunoștințele lor despre ordinea operațiunilor pentru a efectua calcule care implică cele patru operațiuni
note și îndrumări nestatutare:
- rezolva problemele care implică adunare, scădere, înmulțire și împărțire
- utilizați estimarea pentru a verifica răspunsurile la calcule și de a determina, în contextul unei probleme, un grad adecvat de precizie.
idei de lecții de diviziune Anul 6
Sophie Bartlett (@_missiebee) a creat un blog excelent aici (link către blogul lui Sophie despre predarea diviziei lungi) detaliind modul în care va preda divizia lungă pentru o clasă de Anul 6. Deoarece diviziunea lungă este singura nouă învățare pe diviziune pentru anul 6, acesta este un mod ideal de a introduce procedura divizării lungi.
întrebări despre diviziune Anul 6
o problemă tipică a cuvântului de diviziune pe care o va întâlni un student din anul 6 ar fi:
o școală a ridicat 3.146 de la o vânzare de coacere. La eveniment au participat 104 părinți. Dacă toți părinții au cheltuit o sumă egală de bani, cât a cheltuit fiecare părinte?
aici, elevii ar fi de așteptat să folosească metoda diviziunii lungi pentru a rezolva această întrebare pentru a obține răspunsul 30.25.
Divizia: raționament și rezolvarea problemelor Anul 6
cu ceva procedural precum diviziunea lungă, o activitate bună de raționament este de a-i determina pe elevi să găsească greșeli. Aceste resurse oferă o bancă mare de astfel de activități. După cum putem vedea din întrebarea de mai jos, elevii au făcut toată munca grea, dar o eroare neglijentă în numărarea grupurilor de 59 înseamnă că copilul credea că 59 x 7 era 472 și nu 59 x 8.
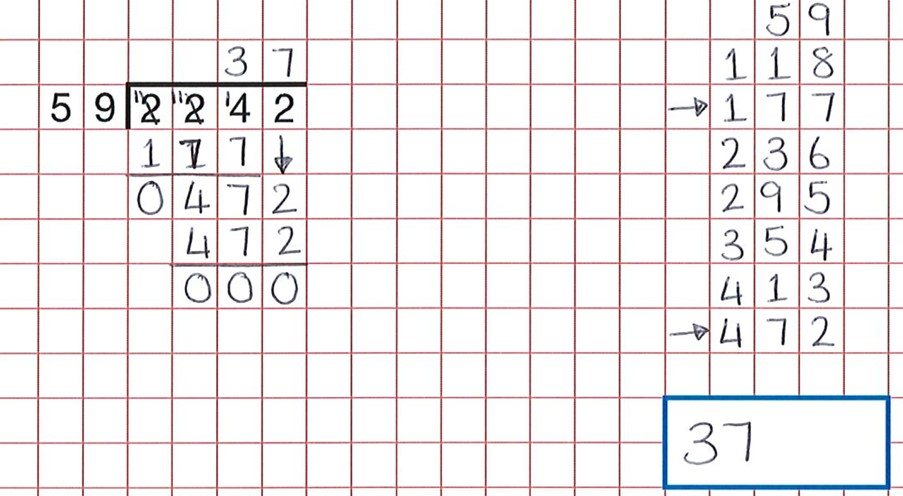
răspunsul corect ar fi fost 38.
diviziunea este un subiect cheie de matematică, nu doar la KS2, ci în matematică în ansamblu. Sperăm că această postare v-a oferit câteva idei bune pentru a vă ajuta elevii să o abordeze cu încredere.
lecții de matematică Online 1-la-1 de încredere de către școli și profesori
în fiecare săptămână, tutorii specializați în matematică ai Third Space Learning susțin mii de copii din școala primară cu lecții săptămânale online 1-la-1 și intervenții matematice. Din 2013 am ajutat peste 100.000 de copii să devină matematicieni mai încrezători și mai capabili. Aflați mai multe sau solicitați o ofertă personalizată pentru a ne vorbi despre nevoile dvs. și despre modul în care vă putem ajuta.
școlarizarea școlară primară vizează nevoile fiecărui copil și urmărește îndeaproape Curriculumul Național.