i den här guiden kommer jag att förklara vad standardfelformeln är och hur man använder den för att räkna ut standardfelet genom att använda ett exempel.
vad är standardfelet?
standardfelet (se), ibland kallat standardfelet för medelvärdet (SEM), är en statistik som motsvarar standardavvikelsen för en provtagningsfördelning i förhållande till medelvärdet. Men vad är det egentligen?
säg att du är intresserad av medelåldern människor i Storbritannien diagnostiseras med Alzheimers sjukdom. Det är inte möjligt att bestämma detta för alla i Storbritannien, därför tar forskare en provpopulation för att generalisera en övergripande siffra. Till exempel kan 10 000 brittiska personer med sjukdomen analyseras och kommer att användas för att generera medelåldern för diagnos. Om du gör detta på ett slumpmässigt urval av 5000 patienter kan du få en medelålder för diagnos på 61,5 år. Men om du gör provanalysen på ett separat slumpmässigt urval av 10 000 andra patienter kan du få en medelålder på 62,3 år. Låt oss säga, hypotetiskt sett naturligtvis, att om du kunde analysera alla människor i Storbritannien som har Alzheimers sjukdom för att få den faktiska siffran, kan du sluta med 64,3 år. Du kan märka att siffrorna från provpopulationerna (61,5 och 62,3 år) skiljer sig från den faktiska siffran (64,3 år). Denna variation i medelvärden förväntas, och när du ökar antalet personer i din provpopulation får du ett värde som ligger närmare den faktiska siffran. Detta är precis vad standardfelet representerar. Standardfelet betyder denna variation i medelvärdena mellan provpopulationerna.
för vidare läsning föreslår jag att du läser den korta Statistikanteckningen av professorerna Douglas Altman och Martin Bland publicerad i British Medical Journal. Det är en bra inblick i vad standardfelet är och vad skillnaden med standardavvikelsen.
standardfelformeln
för att beräkna standardfelet måste du ha två bitar av information: standardavvikelsen och antalet prover i datamängden. Standardfelet beräknas genom att dividera standardavvikelsen med kvadratroten av antalet prover.
här är den fullständiga annoterade standardfelformeln:
exempel
för att förstå standardfelformeln bättre kan det hjälpa till att gå igenom ett exempel. Säg att vi har en befolkning på 80 personer och vi är intresserade av deras höjd. Vi mäter deras höjd och beräknar standardavvikelsen som 30,6 cm. Vi måste nu ansluta dessa värden till vår ekvation:
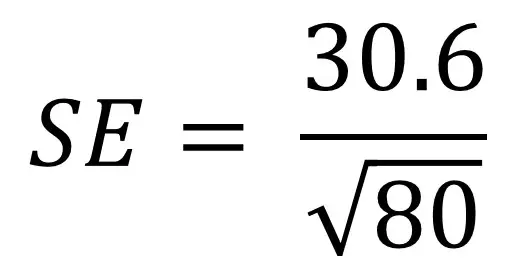om du är obekväm med att mata in ekvationer i miniräknare kan du bryta ner formeln i hanterbara bitar. Här är de steg du kan ta.
- beräkna först kvadratroten av antalet prover (n). I detta fall är n 80. Kvadratroten på 80 är 8,94.
- dela sedan standardavvikelsen (30,6) med kvadratroten på 80 (8,94). Att göra detta ger ett värde på 3,42.
- därför är standardfelet i vår befolkning för höjd 3,42 cm.