Division I Key Stage 2 utgör den sista delen av ’fyra operationer’ – de fyra centrala matematiska begreppen eleverna bör känna till. Den här bloggen hjälper dig att se till att alla dina elever, från år 3 till år 6, kan närma sig division med det förtroende de behöver för att lyckas.
Division I KS2 matematik bygger på vad som har lärt sig på KS1. I slutet av Y2 studenter vid den förväntade standarden kommer att kunna ’ återkalla och använda multiplikation och division fakta för 2, 5 och 10 multiplikationstabellen, inklusive att känna igen udda och jämna tal.’
för lärare i årskurs 3 är det alltid bra att se till att eleverna känner till dessa mycket väl. Med det menar jag inte bara att de kan papegoja delningsfakta på dig, men de förstår verkligen hur man representerar dessa fakta både med konkreta representationer, verbala förklaringar och genom andra bildmetoder.
studenter som inte kan göra detta, men ändå kan muntligt berätta delningsfakta, ha en mycket grund förståelse för division och för att de ska kunna gå vidare till svårare problemlösningsaktiviteter, fördjupa sin konceptuella förståelse för division är ett måste vid År 3.
den nationella läroplanen placerar division inom samma avsnitt som multiplikation i år 3-5 och placerar den inom ett avsnitt som heter ’fyra operationer’ under år 6. De delar som tas från den nationella läroplanen avser endast de som specifikt nämner division. De andra elementen i dessa avsnitt finns i bloggen om multiplikation eller addition och subtraktion där så är lämpligt.
Vad Är Division?
Division är en av de fyra operationerna – de fyra centrala matematiska begreppen som eleverna borde veta-tillsammans med addition och subtraktion och multiplikation.
där multiplikation kombinerar ett nummer flera gånger är division motsatt: räkna ut hur många gånger ett nummer finns i en annan. Att dela 10 med 2 frågar till exempel hur många gånger 2 finns inom 10.

från Third Space Learning ’ s online maths interventions.
Teaching Division KS2-teorin
Division är inversen av multiplikation. Som med multiplikationsbloggen innehåller undervisningen i division tre underliggande strukturer, som i kombination med divisionsfakta och konceptuell förståelse ger eleverna den bästa möjligheten att lyckas när de löser problem relaterade till division.
de tre strukturerna delar, grupperar och skalar. Även om det inte finns tillräckligt med tid att utforska dessa på djupet, vad som följer kommer att vara bara en kort introduktion till dem.
delning och gruppering är inversen av multiplikation som upprepad tillsats. Delning är ett strukturellt koncept som introduceras i KS1 och tidigare där, som namnet antyder, ett belopp delas i lika grupper.
till exempel delas 12 äpplen mellan 3 studenter. Hur många äpplen får varje elev? Här vet vi hela beloppet (12 äpplen) och avgörande, vi vet hur det belopp vi kommer att dela in (3). Beroende på var eleverna är på sin matematiska resa kan de upprepade gånger subtrahera med något tal (1, 2, 3 eller 4) från beloppet i tre högar som representerar de tre studenterna.
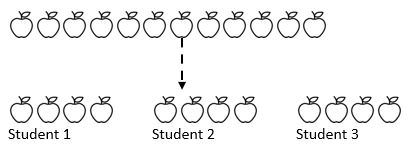
som vi kan se från ovanstående har hela beloppet delats in i tre lika stora grupper.
gruppering liknar delning men det vi vet är något annorlunda jämfört med delning. I delningsstrukturen vet vi hur många grupper som delningen kommer att äga rum. I grupperingsstrukturen vet vi beloppet i varje grupp men inte antalet faktiska grupper som finns.
till exempel delas 12 äpplen i grupper om 4. Hur många grupper kommer det att finnas? Även om denna fråga är mycket lik den ovan, tar den nu gruppstrukturen eftersom vi vet hur många som kommer att gå in i varje grupp men inte längre vet hur många grupper det nu kommer att finnas.
eftersom vi vet att det finns 4 i varje grupp kan vi gruppera 4 äpplen tills vi har täckt alla 12 för att se att det finns 3 grupper.
den slutliga uppdelningsstrukturen är skalning. Medan vi i multiplikation skalar upp ett värde, skalar divisionsstrukturen ner. Till exempel har Shannen 6 pennor och Jen har 3 gånger så färre. Hur många pennor har Jen?
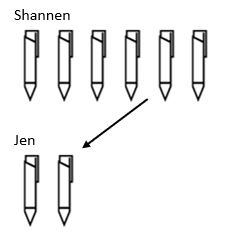
här kan vi se att för att hitta den totala mängden pennor som Jen har, var vi tvungna att ta det belopp som Shannen hade och minska det med en skalfaktor på 3 så att Jen slutar med 2 pennor.
av erfarenhet är detta den svåraste uppdelningsstrukturen för studenter att förstå och förstå och är en som måste ses över i samband med skalning som multiplikation eftersom detta är en avgörande färdighet när man konverterar mätningar och valutor från en större mängd till en mindre mängd. T. ex. kilometer till miles.
Division år 3
i den nationella läroplanen för matematik i England, för varje område av matematik som beskrivs, finns det både ett lagstadgat element och ett icke-lagstadgat element. Det lagstadgade elementet är följande:
- minns och använda multiplikation och division fakta för 3, 4 och 8 multiplikationstabeller
- skriv och beräkna matematiska uttalanden för multiplikation och division med hjälp av multiplikationstabeller som de vet, bland annat för tvåsiffriga tal gånger ensiffriga tal, med hjälp av mentala och utvecklas till formella skriftliga metoder
- lösa problem, inklusive saknade nummerproblem, som involverar multiplikation och division, inklusive positiva heltal skalningsproblem och korrespondensproblem där n objekt är anslutna till m objekt.
icke-lagstadgade anteckningar och vägledning:
- eleverna utvecklar effektiva mentala metoder, till exempel med hjälp av kommutativitet och associativitet (till exempel, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) och multiplikation och division fakta (till exempel med hjälp av 3 × 2 = 6, 6 ÷ 3 = 2 och 2 = 6 2ubbi 3) för att härleda relaterade fakta (till exempel, 30 × 2 = 60, 60 ÷ 3 = 20 och 20 = 60 2BG 3).
- eleverna utvecklar tillförlitliga skriftliga metoder för multiplikation och division, som börjar med beräkningar av tvåsiffriga tal med ensiffriga tal och går vidare till de formella skriftliga metoderna för kort multiplikation och division.
- eleverna löser enkla problem i sammanhang, bestämmer vilken av de fyra operationerna som ska användas och varför. Dessa inkluderar mätning och skalning av sammanhang, (till exempel fyra gånger så höga, åtta gånger så långa etc.) och korrespondensproblem där M-objekt är anslutna till n-objekt (till exempel 3 hattar och 4 rockar, hur många olika kläder?; 12 godis delas lika mellan 4 barn; 4 kakor delas lika mellan 8 barn).
Division aktiviteter år 3
detta kommer inte att täcka en lektion i sig, men ger en guide om hur division kan läras med viss konceptuell förståelse i detta skede. En förutsättning för detta skulle vara undervisning i relaterade multiplikation fakta först innan undervisning någon relaterad division.
när man tänker på strukturer är det bäst på den här delen av elevernas inlärningsresa att hålla fast vid gruppering och delning. För följande exempel kommer vi att titta på att utveckla elevernas förståelse för att dela med 4. Det kommer att följa det konkreta-bildliga-abstrakta tillvägagångssättet.
det är ofta elevernas förståelse av antal som kan begränsa deras framsteg i division. Särskilt när det gäller att gruppera och dela när de bara tar bort en kontinuerligt från helheten.
från början av undervisningsavdelningen bör lärare luta sig på vad eleverna redan vet om jämntal och andra nummerfakta för att utveckla eleverna på att räkna i vilket nummer som helst som är lämpligt.
räknare kan användas för att demonstrera relaterade divisionsfakta eftersom studenter kommer att ha använt avhandlingar när de bygger sin konceptuella förståelse för multiplikation. Frågor som, ’ hur många grupper av 4 finns det?’och’ hur många finns det i varje grupp?’bör ställas och svaren bör relatera till hur detta visar division.
lärare: hur många räknare finns det?
Barn: Fyra
Lärare: Bra. Detta är en grupp på fyra. Hur många grupper om fyra finns det?
Barn: En
Lärare: Utmärkt. Vi har fyra räknare i en grupp. Vi har grupperat fyra räknare i en grupp. Vad har vi gjort?
barn: grupperade fyra räknare i en grupp.
Lärare: Lysande. När vi grupperar fyra räknare i en grupp har vi gjort den matematiska beräkningen av fyra dividerat med en. Vilken beräkning gjorde vi?
barn: fyra dividerat med en.
lärare: och när vi löser fyra dividerat med en är svaret fyra eftersom vi har gjort en grupp som har fyra objekt i den. Fyra dividerat med en är fyra. Vad är fyra dividerat med en?
barn: Fyra dividerat med en är fyra.
Lärare: utmärkt
du kan se hur det skulle upprepas för följande:
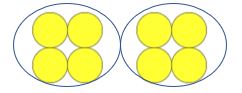
lärare: hur många räknare finns det?
barn: åtta
lärare: bra, det här är en grupp på fyra. Hur många grupper om fyra finns det?
Barn: Två
Lärare: Utmärkt. Vi har fyra räknare i en grupp. Vi har grupperat fyra räknare i två grupper. Vad har vi gjort?
barn: grupperade fyra räknare i två grupper.
Lärare: Lysande. När vi grupperar fyra räknare i två grupper har vi gjort den matematiska beräkningen av åtta dividerat med två. Vilken beräkning gjorde vi?
barn: åtta dividerat med två.
lärare: och när vi löser åtta dividerat med två är svaret fyra eftersom vi har gjort två grupper som har fyra objekt i den. Åtta dividerat med två är fyra. Vad är åtta dividerat med två?
barn: åtta dividerat med två är fyra.
Lärare: utmärkt
när eleverna börjar bli säkra på detta kan vi gå vidare till andra modeller som Cuisenaire rods.

här är hela beloppet representerat i topptåget och den lila stången (som i detta fall representerar 4 och om du har läst andra bloggar i den här serien förhoppningsvis kommer du att veta hur mycket av en förespråkare jag är för deras användning i klassrummet och så kommer eleverna att vara medvetna om dess värde då) används för att visa hur många grupper om 4 som kan gå in i det totala beloppet.
eleverna kan sedan gå vidare till att rita ut scenarier som läses av läraren. Exempelvis. Det finns 24 knappar och de måste grupperas i 4. Hur många grupper finns det? Eleverna kunde dra dessa knappar och gruppera dem i 4 etc.
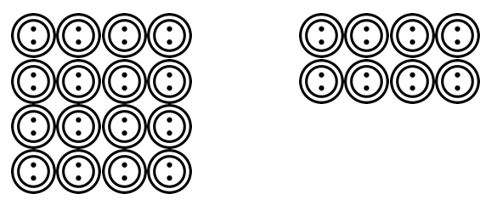
när eleverna har blivit vana vid att kunna visualisera dessa grupperings-eller delningsscenarier i en rad olika sammanhang, kan de gå vidare till mer abstrakta representationer med hjälp av matematiska symboler.

3 Long Division kalkylblad för år 3-6
få dina elever prepped för long division hela KS2 med dessa long division kalkylblad.
Delningsordproblem år 3
ordproblem i år 3 använder vanligtvis grupperings-eller delningsstrukturen.
det finns 40 kakor och 10 studenter. Hur många kakor skulle varje elev få?
eftersom vi vet hur många grupper Det finns (10) måste vi räkna ut beloppet per grupp, så det här är en delningsstruktur. Studenter förväntas använda sin kunskap om 4 gånger tabellen för att lösa detta och få svaret 4.
sektion: Resonemang och problemlösning år 3
för resonemang och problemlösning är en bra aktivitet jag tycker att matcha ett ordproblem till en beräkning. Till exempel:
matcha ordet problem som löses genom att veta 20 dividerat med 4.
- det finns 20 pennor och de kommer att placeras i förpackningar om 5. Hur många i varje förpackning?
- det fanns 20 pennor och sedan tar en student in 4 till. Hur många pennor finns det nu?
- det finns 20 pennor och de kommer att placeras i förpackningar om 4. Hur många i varje förpackning?
- det fanns 20 pennor och sedan saknas 4. Hur många pennor finns det nu?
att få eleverna att skriva ner sina förklaringar för varje fråga är användbart eftersom det gör det möjligt att se deras tänkande. Frågorna har valts noggrant så att siffrorna i varje fråga relaterar till siffrorna på frågan så att eleverna litar på sina matematiska färdigheter för att härleda rätt svar.
Division år 4
i den nationella läroplanen för matematik i England, för varje område av matematik som beskrivs, finns det både ett lagstadgat element och ett icke-lagstadgat element. Det lagstadgade elementet är följande:
- minns multiplikations-och delningsfakta för multiplikationstabeller upp till 12 12 1809>
- använd platsvärde, kända och härledda fakta för att multiplicera och dela mentalt, inklusive: multiplicera med 0 och 1; dividera med 1; multiplicera tillsammans tre siffror
icke-lagstadgade anteckningar och vägledning:
- eleverna fortsätter att öva på att återkalla och använda multiplikationstabeller och relaterade divisionsfakta för att underlätta flyt.
- eleverna utövar mentala metoder och utvidgar detta till tresiffriga tal för att härleda fakta, (till exempel kan 600 3 = 200 2 x 3 = 6).
- eleverna tränar för att bli flytande i den formella skriftliga metoden för kort multiplikation och kort division med exakta svar
- eleverna löser tvåstegsproblem i sammanhang, väljer lämplig operation, arbetar med allt hårdare tal. Detta bör omfatta korrespondens frågor såsom antalet val av en måltid på en meny, eller tre kakor delas lika mellan 10 barn.
Division Lektionsideer år 4
för den här lektionen kommer jag att titta på hur du kan börja lära dig kort division med hjälp av manipulativ bredvid den.
säg att vi ska lära eleverna kort division för frågan 168 dividerat med 12.
vi skulle normalt skriva detta i vad som vanligtvis kallas busshållplats. Men det som är intressant är att olika platser i världen skriver det annorlunda.
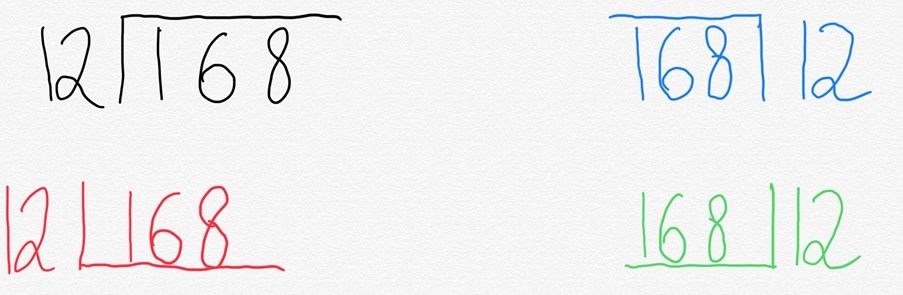
anledningen till detta är ganska enkelt. Vad ’busshållplatsen’ faktiskt representerar är ett förkortat sätt att representera en rektangel.
när vi undervisar formell kort division vad vi effektivt säger är att du måste föreställa dig en rektangel där bredden är 12. Rektangelns totala yta är 168 och vi försöker hitta den saknade längden över toppen. Så hur visar vi detta med hjälp av manipulativ? Dienes block är ett användbart verktyg för detta.
vi vet att det totala beloppet är 168. Så vi måste samla 168 värde av Diener med de minsta mängderna av block som möjligt. Detta visas nedan.
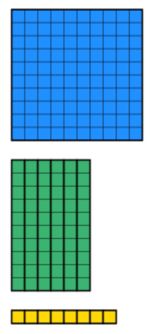
när vi tittar tillbaka på frågan vet vi att bredden är 12. Det betyder att vi nu måste manipulera blocken så att vi får en bredd på 12. Notera, att rektangeln, måste vara fast och kan inte ha några saknade delar. Till exempel skulle nedanstående inte tillåtas trots att det finns 12 enheter som går ner i bredden.
istället kan eleverna rotera två 10s-block för att få följande. Lägg märke till hur det finns 12 i varje kolumn och det är ett fast föremål.
den sista delen eleverna måste göra är att använda de återstående blocken för att skapa en såld rektangel samtidigt som bredden 12. Det kan ta lite tid men med övning blir eleverna snabbare. Efter en tid kommer eleverna att producera detta:
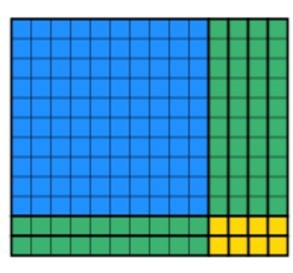
vi kan se att alla 168-värde av block har använts och att bredden fortfarande är 12. För att hitta svaret måste eleverna räkna längden, vilket i detta fall är 14. Jag har överlagrat båda metoderna nedan så att du kan se hur de kompletterar varandra nedan.
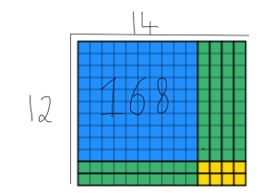
Detta är en användbar strategi för att undervisa studenter i år 4 eftersom det finns massiva återverkningar på andra områden i läroplanen som redan är upplysta för studenter.
även om de kanske inte känner igen det ännu, genom att undervisa kort division som denna har de redan introducerats till omkrets och område – tänk hur mycket undervisningstid som kan sparas när denna anslutning görs. Inte bara det, men i sekundärt, övergår detta tillvägagångssätt till algebraiskt tänkande.
Division Word Problem år 4
studenter förväntas dra nytta av sin kunskap om platsvärde för att lösa divisionsbaserade problem och så skulle ett lämpligt ordproblem vara.
en fruktträdgård odlade 4800 äpplen under en säsong. De placeras i förpackningar om 4 innan de går till marknaden. Hur många förpackningar finns det?
här ska eleverna använda det faktum att 4 x 12 = 48 och som 4,800 är hundra gånger mer än 48, 12 måste också multipliceras med 100 för att få 1,200
Division: Resonemang och problemlösning år 4
är det alltid, ibland eller aldrig sant att summan av tre jämna tal är delbar med 4?
denna fråga ger eleverna gott om möjligheter att experimentera inom parametrarna för frågan. Studenter som behöver mer stöd kan titta på sing digit even numbers och eleverna kan gå upp till vad de känner sig bekväma med.
med öppna frågor som detta är det bra att ge ett minimikrav för hur många försök eleverna ska göra annars kommer de ofta att välja att göra det minsta.
svaret på denna fråga är ibland.
ett snabbt ’trick’ för att veta om ett tal är delbart är att titta på de sista 2 siffrorna i numret och se om de är delbara med 4. Till exempel, om ett barn hittade summan av 34, 36 och 38 och fick 108, som lärare vet jag att detta nummer är delbart med 4 eftersom de sista två siffrorna (08) Gör 8 och är delbara med 4. Om ett barn valde 34, 36 och 48 för att få 118, vet jag att detta inte är delbart med 4 Eftersom 18 – de sista två siffrorna i 118 – inte är delbara med 4.
Division år 5
i den nationella läroplanen för matematik i England, för varje område av matematik som beskrivs, finns det både ett lagstadgat element och ett icke-lagstadgat element. Det lagstadgade elementet är följande:
- multiplicera och dela siffror mentalt med hjälp av kända fakta
- dela upp siffror upp till 4 siffror med ett ensiffrigt nummer med hjälp av den formella skriftliga metoden för kort uppdelning och tolka rester på lämpligt sätt för sammanhanget
- multiplicera och dela heltal och de som involverar decimaler med 10, 100 och 1000
- lösa problem som involverar multiplikation och division inklusive att använda sina kunskaper om faktorer och multiplar, kvadrater och kuber
- lösa problem som involverar addition, subtraktion, multiplikation och division och en kombination av dessa, inklusive att förstå betydelsen av likhetstecknet
- löser problem med multiplikation och division, inklusive skalning med enkla fraktioner och problem med enkla priser.
icke-lagstadgade anteckningar och vägledning:
- eleverna tolkar icke-heltal svar på division genom att uttrycka resultat på olika sätt beroende på sammanhanget, inklusive med remainders, som fraktioner, som decimaler eller genom avrundning (till exempel 98 2BG 4 = = 24 r 2 = 24 = 24,5 25).
- elever använder multiplikation och division som inverser för att stödja införandet av förhållandet i år 6, till exempel genom att multiplicera och dividera med befogenheter på 10 i skalritningar eller genom att multiplicera och dividera med befogenheter på 1000 i omvandling mellan enheter som kilometer och meter.
Division aktiviteter år 5
Division I år 5 fortskrider genom användning av remainders I svar. För den här lektionen kommer jag att titta på en annan användning manipulativ som lärare kan använda för att undervisa 4-by-1-siffrig division.
om frågan var 5,642 dividerat med 4, kan vi representera detta med hjälp av ett platsvärdesdiagram och platsvärderäknare som vi kan se nedan.
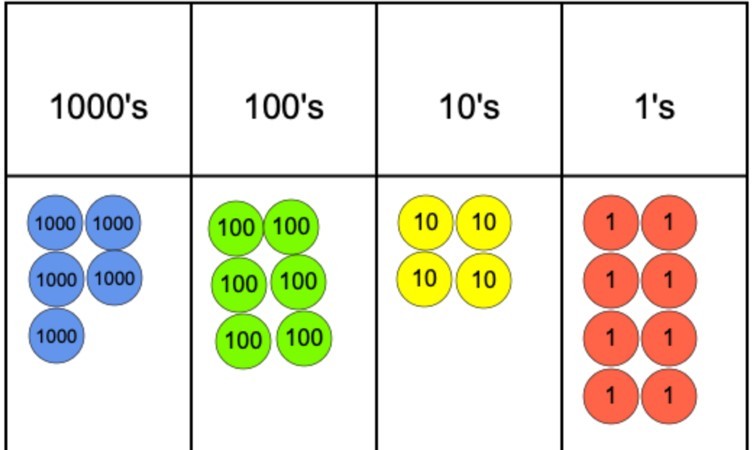
nästa steg skulle vara att börja gruppera räknarna i 4 eftersom det här är vår divisor. Men som det kan ses kommer vi snabbt till ett problem i 1000-talskolumnen eftersom vi kan gruppera 4 av räknarna men då kan vi inte gruppera den återstående räknaren i en grupp av 4.
för att bekämpa denna fråga Kan 1000-räknaren som inte har grupperats bytas ut för tio 100-räknare. Dessa kan sedan grupperas i grupper om 4 och detta kan hända utan att det finns några 100s-räknare kvar. Därifrån är det ett enkelt fall att sedan flytta till 10-talet och slutligen de.
eftersom det finns nio 1s-räknare kan vi gruppera 8 av dem i 2-grupper och 4 och hävda att det finns en kvar*. För att hitta svaret är allt som krävs att räkna antalet grupper som gjorts på varje platsvärde och använda dessa för att skriva siffrorna för att skapa det slutliga svaret. I detta fall skulle svaret vara 1,412 resten 1.
* när du tittar på decimaler kan du byta ut de återstående 1s-räknarna mot tio 0.1-räknare och fortsätta divisionen enligt beskrivningen ovan. Studenter som är bekanta med denna modell är användbara eftersom det kan hjälpa till att avmystifiera division med decimaler som eleverna kan kämpa med. Detta hjälper dem att se att det är en fortsättning på en process som de redan är bekanta med snarare än något nytt.
Divisionsproblem år 5
vid uppdelning i år 5 kommer eleverna att stöta på scenarier där de kommer att behöva runda sitt svar för att svaret ska vara meningsfullt i sammanhanget. En lämplig fråga som visar detta skulle vara något som följande:
en skola planerar ett socialt distanserat disco där de planerar att erbjuda 250 ml juice till varje elev. De kan köpa 2 liter flaskor juice. De förväntar sig 33 studenter att anlända så vet att det kommer att ge ut 8,25 liter juice. Hur många flaskor juice kommer de att behöva köpa?
ett vanligt svar är att eleverna kommer att säga 4 och en fjärdedel. Men eftersom du inte kan köpa en fjärdedel av en flaska, i det här fallet skulle det rätta svaret vara 5 flaskor juice skulle behövas för att säkerställa att alla studenter kunde delta.
Division: resonemang och problemlösning år 5
som nämnts ovan, i år 5, studenter kommer att stöta på scenarier inom division där de kommer att krävas för att välja om ett svar måste avrundas uppåt eller nedåt. Till exempel, när en fråga ber eleverna att räkna ut hur många bussar som behövs för en skola en resa.
att få eleverna att skapa sina egna problem med hjälp av en rad medföljande sammanhang kan vara en riktigt utmanande aktivitet som får eleverna att tänka matematiskt om sammanhang och division.
eleverna kan sedan byta dessa frågor de har skapat med en partner och sedan gå om att lösa dem och kontrollera med den ursprungliga frågan skapare om de har rätt svar.
Division år 6
i den nationella läroplanen för matematik i England, för varje område av matematik som beskrivs, finns det både ett lagstadgat element och ett icke-lagstadgat element. Det lagstadgade elementet är följande:
- dela upp siffror upp till 4 siffror med ett tvåsiffrigt heltal med den formella skriftliga metoden för lång uppdelning och tolka rester som heltalrester, fraktioner eller genom avrundning, beroende på sammanhanget
- dela upp siffror upp till 4 siffror med ett tvåsiffrigt nummer med den formella skriftliga metoden för kort uppdelning där så är lämpligt, tolka rester enligt sammanhanget
- utföra mentala beräkningar, inklusive med blandade operationer och stora siffror
- identifiera gemensamma faktorer, gemensamma multiplar och primtal
- använda sina kunskaper i ordningsföljden för att utföra beräkningar som involverar de fyra operationer
icke-lagstadgade anteckningar och vägledning:
- Lös problem med addition, subtraktion, multiplikation och division
- använd uppskattning för att kontrollera svar på beräkningar och bestämma, i samband med ett problem, en lämplig grad av noggrannhet.
Division Lesson Ideas Year 6
Sophie Bartlett (@_missiebee) har skapat en utmärkt blogg här (länk till Sophie ’ s blog on teaching long division) som beskriver hur hon skulle undervisa long division i ett år 6-klass. Eftersom long division är det enda nya lärandet på division för år 6, är detta ett idealiskt sätt att introducera proceduren för long division.
Division frågor år 6
en typisk division ord problem som ett år 6 student skulle komma över skulle vara:
en skola upp 3,146 från en bake försäljning. 104 föräldrar deltog i evenemanget. Om alla föräldrar spenderade lika mycket pengar, hur mycket spenderade varje förälder?
här förväntas eleverna använda long division-metoden för att lösa denna fråga för att få svaret på 30.25-talet.
Division: resonemang och problemlösning år 6
med något procedurellt som long division är en bra resonemangsaktivitet att få eleverna att hitta misstag. Dessa resurser ger en stor bank av sådan verksamhet. Som vi kan se från frågan nedan har eleverna gjort allt det hårda arbetet men ett slarvigt fel i att räkna grupperna på 59 betyder att barnet trodde att 59 x 7 var 472 och inte 59 x 8.
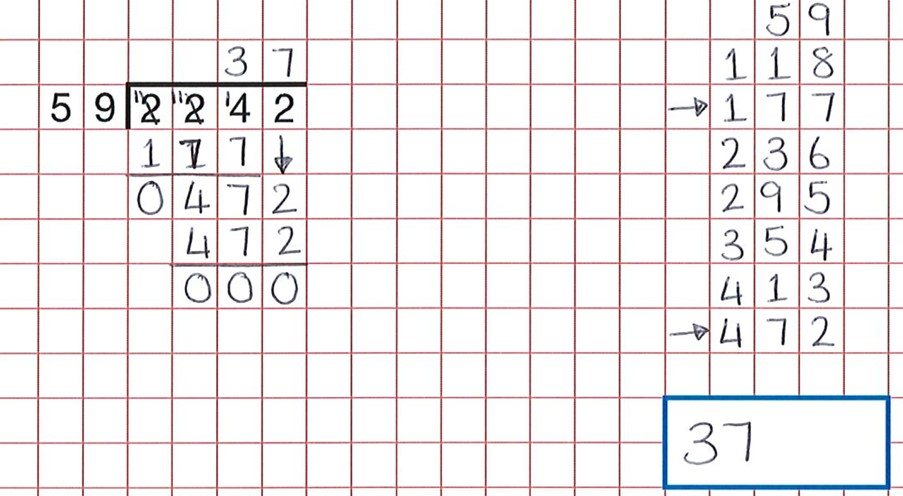
det rätta svaret skulle ha varit 38.
Division är ett viktigt matematikämne, inte bara vid KS2 utan i matematik som helhet. Förhoppningsvis har det här inlägget gett dig några bra ideer för att hjälpa dina elever att närma sig det med självförtroende.
Online 1-till-1-matematiklektioner som är betrodda av skolor och lärare
varje vecka stöder Third Space Learning ’ s maths specialist tutors tusentals grundskolebarn med veckovisa online 1-till-1-lektioner och matematikinterventioner. Sedan 2013 har vi hjälpt över 100 000 barn att bli mer självsäkra, kapabla matematiker. Läs mer eller begär en personlig offert för att prata med oss om dina behov och hur vi kan hjälpa till.
Grundskoleundervisning riktad mot varje barns behov och följer noggrant den nationella läroplanen.