vrcholy, tváře a hrany přicházejí hodně v geometrii základní školy, když se děti učí o vlastnostech 3d tvarů. Zde vysvětlíme, co každý z nich znamená a jak zjistit počet vrcholů, ploch a hran pro jakýkoli tvar. Zahrnujeme také počet hran, ploch a vrcholů nejběžnějších tvarů.
tato slovní zásoba je zavedena v Národním vzdělávacím programu ve 2. ročníku, a proto mohou být následující informace použity u žáků v průběhu let základní školy. Dokonce i rok 1 žáci se mohou začít zabývat vlastnostmi tvarů tímto způsobem, pokud jim chcete dát náskok!
co jsou vrcholy ve tvarech?
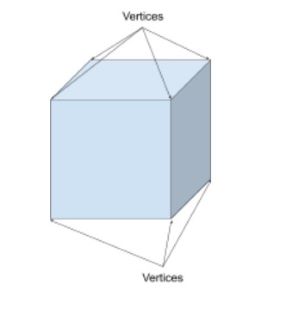
vrcholy ve tvarech jsou body, kde se setkávají dva nebo více úseček nebo hran (jako roh). Singulární vrcholů je vrchol. Například krychle má 8 vrcholů a kužel má jeden vrchol.
vrcholy se někdy nazývají rohy, ale při práci s 2D a 3D tvary je preferováno slovo vrcholy.
krychle má 8 vrcholů. 7 jsou zde viditelné a jeden je skrytý.
co jsou hrany?
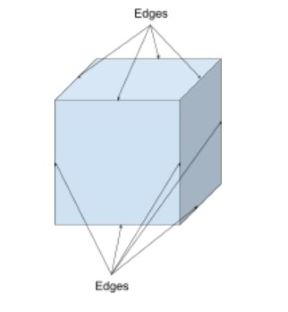
hrany jsou segmenty čáry, které spojují jeden vrchol s druhým a jsou také tam, kde se setkávají tváře tvaru. Ty lze použít k popisu 2d a 3d tvarů.
ačkoli mnoho tvarů má přímé linie a rovné hrany, existují tvary, které mají zakřivené hrany, jako je polokoule. Krychle bude mít 12 rovných okrajů, jak je vidět níže; 9 jsou viditelné a 3 jsou skryté.

zdarma 3D tvary nezávislé Rekapitulace listy
Pomozte svým žákům roku 2 (a starším) revidovat vrcholy, tváře a hrany pomocí našich bezplatných nezávislých Rekapitulačních listů.
co jsou tváře?
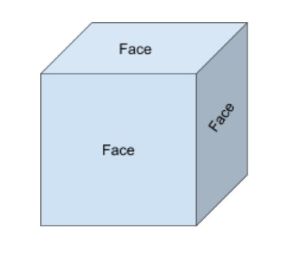
plochy jsou plochý povrch pevného tvaru. Například kvádr má 6 tváří. Když přemýšlíte o 2d a 3d tvarech, je důležité vědět, že 2d tvar představuje pouze tvář 3d tvaru.
je také důležité vědět, že vzhledem k tomu, že naše realita je konstruována ve 3 rozměrech, není možné fyzicky zvládnout 2d tvary, protože jsme obklopeni 3rozměrnými tvary. Pokud je tedy ve vaší třídě zásuvka označená „2d tvary“, měla by být odstraněna, protože učí děti mylné představě. Ačkoli interaktivní koncept pro učebnu, 2d tvary mohou existovat pouze jako 2 rozměrové kresby.
můžete mít ploché i zakřivené plochy, ale považuji za užitečné odkazovat na zakřivené plochy jako zakřivené plochy, protože dobře odpovídá vizuálu tvaru.
existují tři plochy, které jsou viditelné a tři, které jsou skryty na krychli níže.
vrcholy, plochy a hrany běžných 3D tvarů
kolik ploch, hran a vrcholů má kvádr?
kvádr má 8 vrcholů.
kvádr má 12 hran.
kvádr má 6 tváří.

kolik ploch, hran a vrcholů má válec?
válec má 0 vrcholů.
válec má 2 hrany.
válec má 2 plochy a 1 zakřivený povrch.

kolik ploch, hran a vrcholů má polokoule?
polokoule má 0 vrcholů.
polokoule má 1 zakřivenou hranu.
polokoule má 1 obličej a 1 zakřivený povrch.

kolik ploch, hran a vrcholů má kužel?
kužel má 1 vrchol.
kužel má 1 hranu.
polokoule má 1 obličej a 1 zakřivený povrch.

kolik ploch, hran a vrcholů má čtyřstěn?
čtyřstěn má 4 vrcholy.
čtyřstěn má 6 hran.
čtyřstěn má 4 tváře.

kolik ploch, hran a vrcholů má koule?
koule má 0 vrcholů.
čtyřstěn má 0 hran.
čtyřstěn má 1 zakřivený povrch.

kolik ploch, hran a vrcholů má hranol?
hranol je pevný objekt, geometrický tvar nebo mnohostěn, kde plochy obou konců mají stejný tvar. Jako takový, studenti se během své školní docházky setkají s mnoha typy hranolů. Mezi běžné patří kostky, kvádry, trojúhelníkové hranoly, pětiúhelníkové hranoly a šestihranné hranoly.
| tvar | obrazové | plochy | hrany | vrcholy |
|---|---|---|---|---|
| trojúhelníkový hranol | 5 | 9 | 6 | |
| pětiúhelníkový hranol | 7 | 15 | 10 | |
| šestihranný hranol | 8 | 18 | 12 | |
| Cube |  |
6 | 8 | 12 |
| kvádr |  |
6 | 8 | 12 |
kdy se děti učí o vrcholech, tvářích a hranách na základní škole?
děti musí být formálně seznámeny se slovní zásobou vrcholů, ploch a hran v roce 2 při studiu geometrie. Učitelé se však mohou rozhodnout představit tuto slovní zásobu dříve.
žáci 2. ročníku by měli být schopni:
- identifikujte a popište vlastnosti 3D tvarů, včetně počtu hran, vrcholů a ploch
nestátní pokyny uvádějí, že:
- žáci zpracovávají a pojmenovávají širokou škálu běžných tvarů 2-d a 3-d, včetně: čtyřúhelníků a mnohoúhelníků a kvádrů, hranolů a kuželů a identifikují vlastnosti každého tvaru (například počet stran, počet ploch). Žáci identifikují, porovnávají a třídí tvary na základě svých vlastností a přesně používají slovní zásobu, jako jsou strany, hrany, vrcholy a plochy.
od tohoto okamžiku Národní kurikulum znovu výslovně neodkazuje na vrcholy, tváře a hrany, takže učitelé v jiných ročnících budou muset i nadále používat tuto slovní zásobu při pohledu na tvar
jak se vrcholy, plochy a hrany vztahují k jiným oblastem matematiky?
studenti využijí znalosti vrcholů, ploch a hran při pohledu na 2d tvary i 3d tvary. Vědět, jaké jsou hrany a jejich identifikace na složených tvarech, je zásadní pro nalezení obvodu a oblasti 2d složených tvarů. Je to důležitý základ pro pozdější roky při řešení různých matematických vět, jako je teorie grafů a paraboly.
jak se vrcholy, plochy a hrany vztahují ke skutečnému životu?
jakýkoli objekt v reálném životě má vrcholy, plochy a hrany. Například krystal je osmistěn-má osm ploch, dvanáct okrajů a šest vrcholů. Znalost těchto vlastností pro různé trojrozměrné tvary představuje základ pro různá průmyslová odvětví, jako je architektura, interiérový design, strojírenství a další.
vrcholy, plochy a hrany příklad otázky
1. Vysvětlete, co je vrchol.
(odpověď: vrchol je místo, kde se setkávají dvě čáry)
2. Kolik hran má trojúhelníkový hranol?
(odpověď: 9)
3. Kolik vrcholů má kužel?
(Odpověď: 1 vrchol)
4. Kolik tváří má kvádr? Jaké jsou 2D tvary těchto tváří?
(odpověď: 6 tváří. Mohou mít 2 čtvercové plochy a 4 obdélníkové plochy nebo jen 6 obdélníkových ploch.)
5. Pro všechny běžné hranoly (kostky, kvádry, trojúhelníkové hranoly, pětiúhelníkové hranoly a šestihranné hranoly) přidejte plochy a vrcholy dohromady a odečtěte hrany. Co si všimnete na odpovědích?
(odpověď: Odpověď je vždy 2. Toto je známé jako Eulerův vzorec (počet vrcholů – počet hran + počet tváří = 2)
zajímá Vás, jak vysvětlit svým dětem další klíčovou matematickou slovní zásobu? Podívejte se na náš primární matematický slovník, nebo zkuste tyto:
- co je matematické mistrovství?
- co jsou 2d tvary?
- co jsou 3D tvary?
můžete najít spoustu geometrie plány lekce a tisknutelné pracovní listy pro žáky základních škol na třetí Space Learning Maths Hub.
online lekce matematiky 1-to-1 důvěryhodné školami a učiteli
každý týden učitelé matematiky třetího vesmírného učení podporují tisíce dětí základních škol s týdenními online lekcemi 1-to-1 a matematickými intervencemi. Od roku 2013 jsme pomohli více než 100 000 dětem stát se sebevědomějšími a schopnějšími matematiky. Zjistěte více nebo požádejte o osobní nabídku, abyste s námi mluvili o vašich potřebách a o tom, jak vám můžeme pomoci.
naše online výuka pro matematiku program poskytuje každé dítě s jejich vlastní profesionální jeden na jednoho učitele matematiky