v této příručce vysvětlím, co je standardní chybový vzorec a jak jej použít k vyřešení standardní chyby pomocí příkladu.
jaká je standardní chyba?
standardní chyba (se), někdy označovaná jako standardní chyba průměru (SEM), je statistika, která odpovídá směrodatné odchylce vzorkovacího rozdělení vzhledem ke střední hodnotě. Ale co to vlastně je?
Řekněme, že máte zájem o průměrný věk lidé ve Velké Británii jsou diagnostikováni s Alzheimerovou chorobou. Není možné to určit pro všechny ve Velké Británii, proto vědci odebírají vzorek populace, aby zobecnili celkové číslo. Například 10 000 Britů s touto chorobou může být analyzováno a bude použito ke generování průměrného věku diagnózy. Pokud tak učiníte na náhodném vzorku 5 000 pacientů, můžete získat průměrný věk diagnózy 61,5 let. Pokud však provedete analýzu vzorku na samostatném náhodném vzorku 10 000 dalších pacientů, můžete dosáhnout průměrného věku 62,3 let. Řekněme, hypoteticky řečeno, samozřejmě, že pokud jste byli schopni analyzovat všechny lidi ve Velké Británii, kteří mají Alzheimerovu chorobu, abyste získali skutečné číslo, můžete skončit s 64.3 roky. Můžete si všimnout, že údaje získané z populací vzorků (61, 5 a 62, 3 let) se liší od skutečného čísla (64, 3 let). Očekává se tato změna průměrných hodnot, a jak zvýšíte počet lidí ve vaší populaci vzorku, získáte hodnotu, která je blíže skutečnému číslu. To je přesně to, co představuje standardní chyba. Standardní chyba znamená tuto změnu průměrných hodnot mezi populacemi vzorků.
pro další čtení doporučuji přečíst si krátkou statistickou poznámku profesorů Douglas Altman a Martin Bland zveřejněnou v British Medical Journal. Je to užitečný vhled do toho, co je standardní chyba a jaký je rozdíl se směrodatnou odchylkou.
vzorec standardní chyby
pro výpočet standardní chyby musíte mít dvě informace: směrodatnou odchylku a počet vzorků v datové sadě. Standardní chyba se vypočítá vydělením směrodatné odchylky druhou odmocninou počtu vzorků.
zde je úplný anotovaný vzorec standardní chyby:
příklad
Chcete-li lépe porozumět vzorci standardní chyby, může vám pomoci projít příkladem. Řekněme, že máme populaci 80 lidí a zajímá nás jejich výška. Měříme jejich výšku a vypočítáme směrodatnou odchylku jako 30,6 cm. Nyní musíme tyto hodnoty zapojit do naší rovnice:
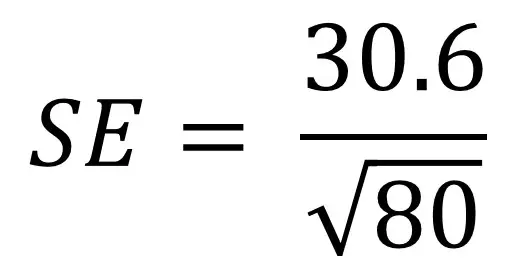pokud se vám nelíbí zadávání rovnic do kalkulaček, můžete vzorec rozdělit na zvládnutelné kousky. Zde jsou kroky, které můžete podniknout.
- nejprve Vypočítejte druhou odmocninu počtu vzorků (n). V tomto případě je n 80. Druhá odmocnina z 80 je 8,94.
- dále vydělte směrodatnou odchylku (30.6) druhou odmocninou z 80 (8.94). To dává hodnotu 3, 42.
- proto je standardní chyba v naší populaci pro výšku 3,42 cm.