divize v klíčové fázi 2 tvoří poslední část “ čtyř operací – – čtyři základní matematické pojmy, které by žáci měli znát. Tento blog vám pomůže zajistit, aby všichni vaši žáci, od roku 3 do roku 6, mohou přistupovat k divizi s důvěrou, kterou potřebují k úspěchu.
dělení v matematice KS2 navazuje na to, co se naučilo na KS1. Do konce roku Y2 studenti na očekávaném standardu budou schopni ‚ vyvolat a používat násobení a dělení fakta pro 2, 5 a 10 multiplikační tabulky, včetně rozpoznávání lichých a sudých čísel.‘
pro učitele v roce 3 je vždy dobré zajistit, aby je studenti velmi dobře znali. Tím nemyslím jen to, že na vás mohou papouškovat fakta o rozdělení, ale skutečně chápou, jak tyto skutečnosti reprezentovat jak konkrétními reprezentacemi, verbálními vysvětleními, tak jinými obrazovými metodami.
studenti, kteří nejsou schopni to udělat, přesto jsou schopni slovně říci fakta o rozdělení, mají velmi mělké porozumění rozdělení a aby mohli postupovat k obtížnějším činnostem řešení problémů, prohloubení jejich koncepčního chápání rozdělení je nutností v roce 3.
Národní kurikulum umístí rozdělení do stejné sekce jako násobení pro roky 3-5 a umístí jej do sekce nazvané „čtyři operace“ v roce 6. Části převzaté z národních učebních osnov se týkají pouze těch, které konkrétně zmiňují rozdělení. Ostatní prvky těchto sekcí lze nalézt v blogu o násobení nebo sčítání a odčítání, kde je to vhodné.
Co Je Divize?
dělení je jednou ze čtyř operací – čtyř základních matematických pojmů, které by žáci měli znát – vedle sčítání a odčítání a násobení.
kde násobení kombinuje jedno číslo vícekrát, dělení je opačné: zjistit, kolikrát je jedno číslo obsaženo v jiném. Například dělení 10 na 2 se ptá, kolikrát je 2 obsaženo v 10.

z online matematických intervencí třetího vesmírného učení.
učební dělení KS2-teorie
dělení je inverzní násobení. Stejně jako u multiplikačního blogu obsahuje Výuka Dělení tři základní struktury, které ve spojení s fakty o dělení a koncepčním porozuměním poskytnou studentům nejlepší příležitost být úspěšní při řešení problémů souvisejících s dělením.
tyto tři struktury jsou sdílení, seskupování a škálování. I když není dost času na to, abychom je podrobně prozkoumali, to, co následuje, bude jen krátký úvod do nich.
sdílení a seskupování jsou inverzní násobení jako opakované sčítání. Sdílení je strukturální koncept, který je zaveden v KS1 a dříve, kde, jak název napovídá, je částka sdílena do stejných skupin.
například 12 jablek je sdíleno mezi 3 studenty. Kolik jablek dostane každý student? Zde známe celou částku (12 jablek) a hlavně víme, do jaké částky se budeme dělit (3). V závislosti na tom, kde jsou studenti na své matematické cestě, mohou opakovaně odečíst nějakým číslem (1, 2, 3 nebo 4) z částky do tří hromádek, které představují tři studenty.
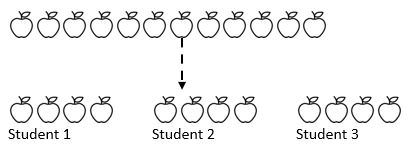
jak vidíme z výše uvedeného, celá částka byla rozdělena do tří stejných skupin.
seskupování je podobné sdílení, ale to, co víme, je mírně odlišné ve srovnání se sdílením. Ve struktuře sdílení víme, kolik skupin bude sdílení probíhat. Ve struktuře seskupení známe částku v každé skupině, ale ne počet skutečných skupin, které existují.
například 12 jablek je sdíleno ve skupinách po 4. Kolik skupin bude? I když je tato otázka velmi podobná té výše uvedené, nyní přebírá strukturu seskupení, protože víme, kolik jich půjde do každé skupiny, ale už nevíme, kolik skupin bude nyní.
protože víme, že v každé skupině jsou 4, můžeme seskupit 4 jablka, dokud nepokryjeme všech 12, abychom zjistili, že existují 3 skupiny.
konečná struktura dělení je škálování. Zatímco v násobení jsme zvětšovali hodnotu, struktura dělení se zmenšuje. Například, Shannen má 6 pera a Jen má 3 krát méně. Kolik má jen propisek?
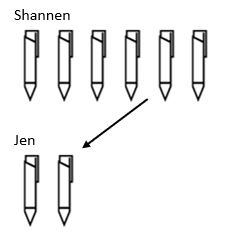
zde vidíme, že k nalezení celkového množství per, které má Jen, jsme museli vzít částku, kterou měl Shannen, a snížit ji o měřítko 3 tak, aby Jen skončila 2 pera.
ze zkušenosti je to nejtěžší struktura dělení, kterou studenti uchopí a pochopí, a je třeba ji znovu navštívit ve spojení s škálováním jako násobením, protože to je zásadní dovednost při převodu měření a měn z většího množství na menší množství. Např. kilometry na míle.
Division Year 3
v Národním kurikulu pro matematiku v Anglii je pro každou nastíněnou oblast matematiky jak zákonný prvek, tak nestatutární prvek. Zákonný prvek je následující:
- vyvolat a používat násobení a dělení fakta pro 3, 4 a 8 násobilky
- psát a vypočítat matematické příkazy pro násobení a dělení pomocí násobilky, které znají, včetně dvoumístných čísel krát jednomístná čísla, pomocí mentální a postupující k formálním písemným metodám
- řešit problémy, včetně chybějících čísel, zahrnující násobení a dělení, včetně kladných celočíselných škálování problémů a korespondence problémy, ve kterých jsou n objekty připojeny k m objektům.
nestátní poznámky a pokyny:
- žáci rozvíjejí efektivní mentální metody, například pomocí komutativity a asociativity (například, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) a násobení a dělení faktů (například pomocí 3 × 2 = 6, 6 ÷ 3 = 2 a 2 = 6 ÷ 3) odvodit související skutečnosti (například, 30 × 2 = 60, 60 ÷ 3 = 20 a 20 = 60 ÷ 3).
- žáci rozvíjejí spolehlivé písemné metody násobení a dělení, počínaje výpočty dvoumístných čísel jednocifernými čísly a postupujícími k formálním písemným metodám krátkého násobení a dělení.
- žáci řeší jednoduché problémy v souvislostech a rozhodují, kterou ze čtyř operací použít a proč. Patří sem kontexty měření a škálování (například čtyřikrát vyšší, osmkrát delší atd.) a problémy s korespondencí, ve kterých jsou M objekty spojeny s n objekty (například 3 klobouky a 4 kabáty, kolik různých oblečení?; 12 sladkostí sdílených rovnoměrně mezi 4 dětmi; 4 dorty sdílené rovnoměrně mezi 8 dětmi).
činnosti divize rok 3
to nepokryje lekci sama o sobě, ale poskytne průvodce, jak lze v této fázi vyučovat dělení s určitým koncepčním porozuměním. Předpokladem pro to by byla výuka souvisejících multiplikačních faktů nejprve před vyučováním jakéhokoli souvisejícího rozdělení.
při přemýšlení o strukturách je nejlepší v této části studijní cesty studentů držet se seskupování a sdílení. V následujících příkladech se podíváme na rozvoj porozumění dělením podle 4. Bude následovat konkrétní-obrazový-abstraktní přístup.
často studenti chápou číslo, které může omezit jejich pokrok v dělení. Zejména pokud jde o seskupování a sdílení, když od celku nepřetržitě odebírají pouze jedno.
Od počátku rozdělení výuky by se učitelé měli opřít o to, co studenti již vědí o sudých číslech a dalších číselných faktech, aby studenti mohli počítat v jakémkoli počtu, který může být vhodný.
čítače mohou být použity k prokázání souvisejících faktů dělení, protože studenti budou při budování koncepčního chápání násobení používat teze. Otázky jako, “ kolik skupin 4 jsou tam? a kolik jich je v každé skupině?“je třeba se zeptat a odpovědi by se měly týkat toho, jak to ukazuje rozdělení.
učitel: kolik čítačů existuje?
Dítě: Čtyři
Učitel: Dobrý. Jedná se o čtyřčlennou skupinu. Kolik je čtyřčlenných skupin?
Dítě: Jeden
Učitel: Výborný. Máme čtyři čítače v jedné skupině. Seskupili jsme čtyři čítače do jedné skupiny. Co jsme to udělali?
dítě: seskupeny čtyři čítače do jedné skupiny.
Učitel: Brilantní. Když seskupíme čtyři čítače do jedné skupiny, provedli jsme matematický výpočet čtyř dělených jedním. Jaký výpočet jsme udělali?
dítě: čtyři děleno jedním.
učitel: a když vyřešíme čtyři děleno jedním, odpověď je čtyři, protože jsme vytvořili jednu skupinu, která má v sobě čtyři položky. Čtyři děleno jedním jsou čtyři. Co je čtyři děleno jedním?
dítě: Čtyři děleno jedním jsou čtyři.
učitel: výborný
můžete vidět, jak by se to opakovalo pro následující:
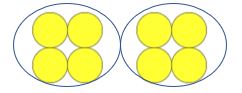
učitel: kolik čítačů existuje?
dítě: osm
učitel: dobrý, To je skupina čtyř. Kolik je čtyřčlenných skupin?
Dítě: Dva
Učitel: Výborný. Máme čtyři čítače v jedné skupině. Seskupili jsme čtyři čítače do dvou skupin. Co jsme to udělali?
dítě: seskupeny čtyři čítače do dvou skupin.
Učitel: Brilantní. Když seskupíme čtyři čítače do dvou skupin, provedli jsme matematický výpočet osmi děleno dvěma. Jaký výpočet jsme udělali?
dítě: osm děleno dvěma.
učitel: a když vyřešíme osm děleno dvěma, odpověď je čtyři, protože jsme vytvořili dvě skupiny, které mají v sobě čtyři položky. Osm děleno dvěma je čtyři. Co je osm děleno dvěma?
dítě: osm děleno dvěma je čtyři.
učitel: výborný
když si s tím studenti začínají být jisti, můžeme přejít k jiným modelům,jako jsou pruty Cuisenaire.

zde je celá částka zastoupena v horním vlaku a fialová tyč (což v tomto případě představuje 4 a pokud jste si přečetli další blogy v této sérii, doufejme, že budete vědět, kolik obhájce jsem pro jejich použití ve třídě, a tak si studenti budou vědomi své hodnoty do té doby) se používá k ukázání, kolik skupin po 4 může jít do celkové částky.
studenti pak mohou přejít na kreslení scénářů čtených učitelem. Příklad. K dispozici je 24 tlačítek a je třeba je seskupit do 4. Kolik je tam skupin? Studenti mohli kreslit tato tlačítka a seskupit je do 4 atd.
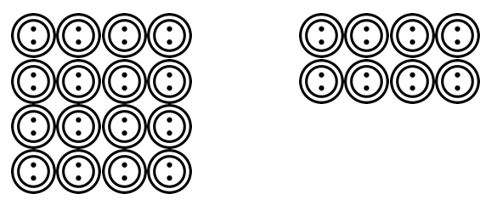
jakmile si studenti zvykli na to, že jsou schopni vizualizovat tyto scénáře seskupování nebo sdílení rozdělení v různých kontextech, mohou přejít k abstraktnějším reprezentacím pomocí matematických symbolů.

3 dlouhé dělící listy pro roky 3-6
Získejte své žáky připravené na dlouhé dělení v KS2 pomocí těchto dlouhých dělících listů.
rozdělení slovní problémy rok 3
slovní problémy v roce 3 se běžně používají seskupování nebo sdílení strukturu.
existuje 40 koláče a 10 studenti. Kolik dortů by každý student dostal?
protože víme, kolik skupin existuje (10), musíme zjistit částku na skupinu, takže se jedná o strukturu sdílení. Od studentů by se očekávalo, že využijí své znalosti tabulky 4 times, aby to vyřešili a dostali odpověď 4.
divize: Uvažování a řešení problémů rok 3
pro uvažování a řešení problémů je dobrá aktivita, kterou považuji za přiřazení slovního problému k výpočtu. Například:
zápas slovo problémy, které jsou řešeny tím, že zná 20 děleno 4.
- existuje 20 tužek a budou umístěny do balení po 5. Kolik v každém balení?
- bylo 20 tužek a pak student přinese další 4. Kolik tužek je teď?
- existuje 20 tužek a budou umístěny do balení po 4. Kolik v každém balení?
- bylo 20 tužek a pak 4 zmizely. Kolik tužek je teď?
přimět studenty, aby si zapsali svá vysvětlení pro každou otázku, je užitečné, protože umožňuje vidět jejich myšlení. Otázky byly vybrány pečlivě tak, aby čísla v každé otázce se vztahují k číslům na otázku, takže studenti se spoléhají na své matematické dovednosti odvodit správnou odpověď.
Division Year 4
v Národním kurikulu pro matematiku v Anglii je pro každou nastíněnou oblast matematiky jak zákonný prvek, tak nestatutární prvek. Zákonný prvek je následující:
- Připomeňme násobení a dělení fakta pro násobilky do 12 × 12
- použijte místo hodnoty, známé a odvozené skutečnosti násobit a rozdělit mentálně, včetně: násobení 0 a 1; dělení 1; násobení dohromady tři čísla
Non-statutární poznámky a pokyny:
- žáci pokračují v procvičování vzpomínek a používání multiplikačních tabulek a souvisejících faktů dělení, aby pomohli plynulosti.
- žáci praktikují mentální metody a rozšiřují je na tříciferná čísla, aby odvodili fakta (například 600 ÷ 3 = 200 lze odvodit z 2 x 3 = 6).
- žáci si procvičují plynulou formální písemnou metodu krátkého násobení a krátkého dělení s přesnými odpověďmi
- žáci řeší dvoufázové problémy v souvislostech, volí vhodnou operaci, pracují se stále těžšími čísly. To by mělo zahrnovat korespondenční otázky, jako je počet možností jídla v nabídce, nebo tři koláče sdílené rovnoměrně mezi 10 děti.
nápady na lekce divize rok 4
pro tuto lekci se podívám na to, jak můžete začít učit krátké dělení pomocí manipulativů vedle něj.
Řekněme, že budeme učit studenty krátké dělení na otázku 168 děleno 12.
normálně bychom to napsali do toho, co se běžně označuje jako autobusová zastávka. Zajímavé však je, že různá místa na světě to píší jinak.
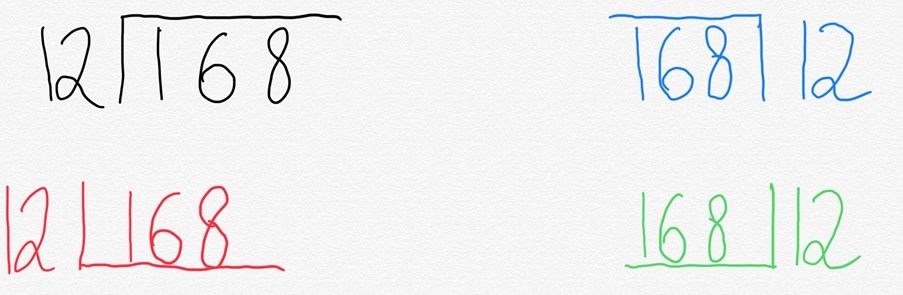
důvod je poměrně jednoduchý. „Autobusová zastávka“ ve skutečnosti představuje zkrácený způsob reprezentace obdélníku.
když učíme formální krátké dělení, účinně říkáme, že si musíte představit obdélník, kde je šířka 12. Celková plocha obdélníku je 168 a snažíme se najít chybějící délku přes vrchol. Jak to tedy ukážeme pomocí manipulativů? Bloky Dienes jsou pro to užitečným nástrojem.
víme, že celková částka je 168. Takže musíme shromáždit 168 dienů za použití co nejmenšího množství bloků. To je uvedeno níže.
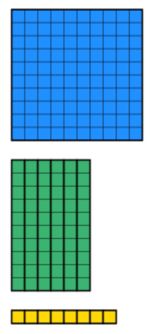
při pohledu zpět na otázku víme, že šířka je 12. To znamená, že nyní musíme manipulovat s bloky tak, abychom získali šířku 12. Všimněte si, že obdélník musí být pevný a nesmí mít žádné chybějící části. Například, níže by nebylo povoleno, přestože existuje 12 jednotky jdou dolů na šířku.
místo toho mohou studenti otočit dva bloky 10s a získat následující. Všimněte si, jak je v každém sloupci 12 a je to pevný objekt.
závěrečná část, kterou musí studenti udělat, je použít zbývající bloky k vytvoření prodaného obdélníku při zachování šířky 12. To může nějakou dobu trvat, ale s praxí se studenti zrychlují. Po nějaké době to studenti vyrobí:
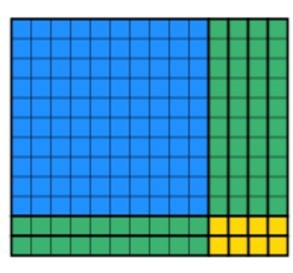
vidíme, že všech 168 bloků v hodnotě byly vyčerpány a že šířka je stále 12. Chcete-li najít odpověď, studenti jsou povinni počítat délku, která je v tomto případě 14. Obě metody jsem překrýval níže, takže můžete vidět, jak se navzájem doplňují níže.
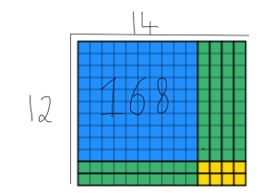
Toto je užitečná strategie pro výuku studentů v roce 4, protože v jiných oblastech učebních osnov, které jsou studentům již osvětleny, existují masivní dopady.
i když to možná ještě nepoznají, vyučováním krátkého dělení, jako je toto, již byli zavedeni do obvodu a oblasti-přemýšlejte, kolik času výuky lze ušetřit, když je toto spojení provedeno. Nejen to, ale v sekundárním případě se tento přístup přenáší na algebraické myšlení.
rozdělení slovní problémy rok 4
od studentů by se očekávalo, že budou čerpat ze svých znalostí hodnoty místa k řešení problémů založených na rozdělení, a tak by byl vhodný slovní problém.
sad vypěstoval za sezónu 4800 jablek. Jsou umístěny v balení po 4 před odchodem na trh. Kolik balení je tam?
zde by studenti měli použít skutečnost, že 4 x 12 = 48 a protože 4 800 je stokrát více než 48, 12 musí také vynásobit 100, aby získali 1 200
: Uvažování a řešení problémů rok 4
je vždy, někdy nebo nikdy pravda, že součet tří sudých čísel je dělitelný 4?
tato otázka dává studentům dostatek příležitostí experimentovat v rámci parametrů otázky. Studenti, kteří potřebují větší podporu, se mohou podívat na sudá čísla sing digit a studenti by mohli jít na to, s čím se cítí dobře.
s otevřenými otázkami, jako je tato, je dobré stanovit minimální požadavek na to, kolik pokusů by studenti měli udělat, jinak se často rozhodnou udělat holé minimum.
odpověď na tuto otázku je někdy.
rychlý „trik“, jak zjistit, zda je číslo dělitelné, je podívat se na poslední 2 číslice čísla a zjistit, zda jsou dělitelné 4. Například, pokud dítě našlo součet 34, 36 a 38 a dostalo 108, jako učitel vím, že toto číslo je dělitelné 4, protože poslední dvě číslice (08)činí 8 a jsou dělitelné 4. Pokud si dítě zvolilo 34, 36 a 48, aby získalo 118, vím, že to není dělitelné 4 jako 18-poslední dvě číslice 118 – nejsou dělitelné 4.
Division Year 5
v Národním kurikulu pro matematiku v Anglii je pro každou nastíněnou oblast matematiky jak zákonný prvek, tak nestatutární prvek. Zákonný prvek je následující:
- vynásobte a vydělte čísla mentálně na základě známých skutečností
- vydělte čísla až 4 číslicemi jednociferným číslem pomocí formální písemné metody krátkého dělení a interpretujte zbytky vhodně pro kontext
- vynásobte a vydělte celá čísla a čísla zahrnující desetinná čísla 10, 100 a 1000
- vyřešte problémy zahrnující násobení a dělení včetně využití jejich znalostí faktorů a násobků, čtverců a kostek
- vyřešte problémy zahrnující sčítání, odčítání, násobení a dělení a kombinace ty, včetně pochopení významu znaménka rovnosti
- , řeší problémy zahrnující násobení a dělení, včetně škálování jednoduchými zlomky a problémy zahrnující jednoduché sazby.
nestátní poznámky a pokyny:
- žáci interpretují neceločíselné odpovědi na dělení vyjádřením výsledků různými způsoby podle kontextu, včetně zbytků, jako zlomků, desetinných míst nebo zaokrouhlením (například 98 ÷ 4 = = 24 r 2 = 24 = 24,5 ≈ 25).
- žáci používají násobení a dělení jako inverzi, aby podpořili zavedení poměru v roce 6, například vynásobením a dělením mocninami 10 ve výkresech měřítka nebo vynásobením a vydělením mocninami 1000 V přepočtu mezi jednotkami, jako jsou kilometry a metry.
činnosti divize rok 5
dělení v roce 5 postupuje použitím zbytků v odpovědích. Pro tuto lekci se podívám na další použití manipulativů, které mohou učitelé použít k výuce 4-by-1-místné dělení.
pokud byla otázka 5 642 děleno 4, mohli bychom to reprezentovat pomocí grafu hodnoty místa a čítačů hodnot místa, jak vidíme níže.
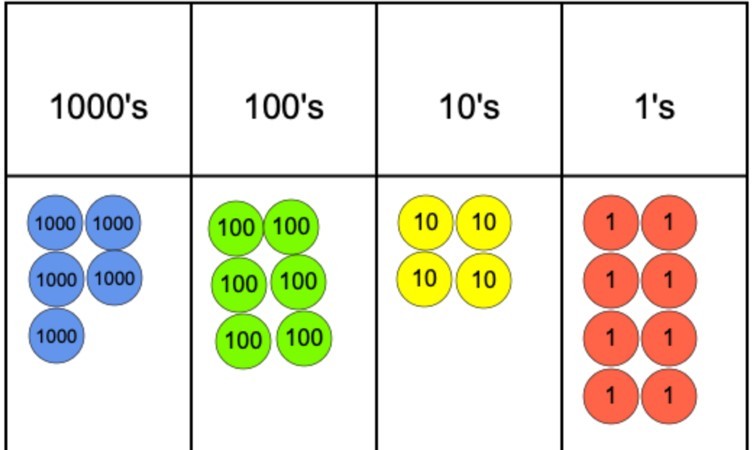
dalším krokem by bylo začít seskupovat čítače do 4, protože to je náš dělitel. Nicméně, jak je vidět, rychle se dostaneme k problému ve sloupci 1000, protože jsme schopni seskupit 4 čítačů, ale pak nemůžeme seskupit zbývající čítač do skupiny 4.
pro boj s tímto problémem lze čítač 1000, který nebyl seskupen, vyměnit za deset čítačů 100. Ty pak mohou být seskupeny do skupin po 4 a to se může stát, aniž by existovaly nějaké čítače 100s. Odtud je to jednoduchý případ, kdy se přesuneme na 10 a nakonec na ty.
protože existuje devět čítačů 1s, můžeme seskupit 8 z nich do 2 skupin a 4 a tvrdit, že zbývá jeden*. Chcete-li najít odpověď, vše, co je potřeba, je spočítat počet skupin vytvořených v každé hodnotě místa a použít je k zápisu číslic k vytvoření konečné odpovědi. V tomto případě by odpověď byla 1 412 1.
* když se díváte na desetinná místa, můžete vyměnit zbývající čítač 1s za deset čítačů 0.1 a pokračovat v dělení, jak je popsáno výše. Studenti, kteří jsou obeznámeni s tímto modelem, jsou užiteční, protože mohou pomoci demystifikovat dělení desetinnými místy, se kterými mohou studenti bojovat. To jim pomáhá vidět, že se jedná o pokračování procesu, který již znají, spíše než o něco nového.
problémy dělení rok 5
při dělení v roce 5 se studenti setkají se scénáři, kde budou muset zaokrouhlit svou odpověď, aby odpověď měla smysl v kontextu. Vhodná otázka, která to dokazuje, by byla něco jako následující:
škola plánuje společenskou diskotéku, kde plánuje nabídnout každému studentovi 250 ml šťávy. Mohou si koupit 2 litrové láhve džusu. Očekávají, že přijede 33 studentů, takže vědí, že vydají 8,25 litru šťávy. Kolik lahví šťávy budou muset koupit?
běžnou odpovědí je, že studenti řeknou 4 a čtvrt. Nicméně, protože si nemůžete koupit čtvrtinu láhve, v tomto případě by správná odpověď byla 5 láhve šťávy by byly potřebné k zajištění toho, aby se všichni studenti mohli účastnit.
divize: uvažování a řešení problémů rok 5
jak je uvedeno výše, v roce 5 se studenti setkají se scénáři v divizi, kde budou muset zvolit, zda je třeba odpověď zaokrouhlit nahoru nebo dolů. Například, když otázka požádá studenty, aby zjistili, kolik autobusů je potřeba pro školu výlet.
přimět studenty, aby si vytvořili vlastní problémy pomocí řady poskytnutých kontextů, může být opravdu náročná aktivita, která přiměje studenty matematicky přemýšlet o kontextu a rozdělení.
studenti si pak mohou tyto otázky, které vytvořili, vyměnit s partnerem a poté je vyřešit a zkontrolovat u původního tvůrce otázek, zda mají správnou odpověď.
Division Year 6
v Národním kurikulu pro matematiku v Anglii je pro každou nastíněnou oblast matematiky jak zákonný prvek, tak nestatutární prvek. Zákonný prvek je následující:
- vydělte čísla do 4 číslic dvoumístným celým číslem pomocí formální písemné metody dlouhého dělení a interpretujte zbytky jako celé číselné zbytky, zlomky nebo zaokrouhlením, podle potřeby pro kontext
- vydělte čísla do 4 číslic dvoumístným číslem pomocí formální písemné metody krátkého dělení, kde je to vhodné, interpretace zbytků podle kontextu
- provádějte mentální výpočty, včetně smíšených operací a velkých čísel
- identifikujte společné faktory, společné hodnoty a hodnoty. násobky a prvočísla
- využijte své znalosti o pořadí operací k provádění výpočtů zahrnujících čtyři operace
nestátní poznámky a pokyny:
- řešení problémů zahrnujících sčítání, odčítání, násobení a dělení
- pomocí odhadu zkontrolujte odpovědi na výpočty a v kontextu problému určete odpovídající stupeň přesnosti.
nápady na lekce divize rok 6
Sophie Bartlett (@_MissieBee) zde vytvořila vynikající blog (odkaz na Sophiin blog o výuce dlouhé divize) s podrobnostmi o tom, jak bude učit dlouhou divizi za rok 6 třída. Dokud je divize jediným novým učením o divizi pro rok 6, je to ideální způsob, jak zavést postup dlouhého dělení.
otázky divize rok 6
typický problém dělení slov, na který by se student roku 6 setkal, by byl:
škola získala 3,146 £z prodeje pečiva. Akce se zúčastnilo 104 rodičů. Pokud všichni rodiče utratili stejné množství peněz, kolik každý rodič utratil?
zde by se od studentů očekávalo, že k vyřešení této otázky použijí metodu dlouhého dělení, aby získali odpověď £30.25.
divize: uvažování a řešení problémů rok 6
s něčím procedurálním, jako je dlouhé dělení, je dobrou argumentační činností přimět studenty, aby našli chyby. Tyto zdroje poskytují velkou banku takových činností. Jak vidíme z níže uvedené otázky, studenti odvedli veškerou tvrdou práci, ale neopatrná chyba při počítání skupin 59 znamená, že dítě věřilo, že 59 x 7 bylo 472 a ne 59 x 8.
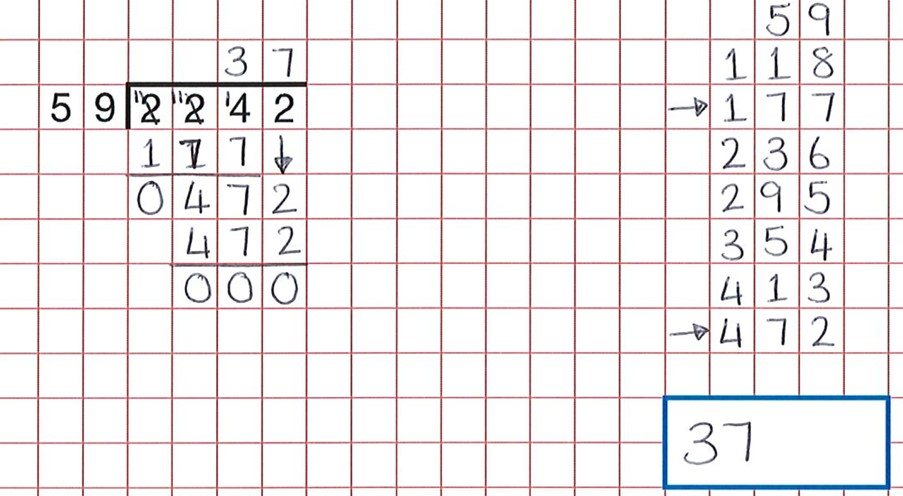
správná odpověď by byla 38.
dělení je klíčovým matematickým tématem nejen v KS2, ale i v matematice jako celku. Doufejme, že tento příspěvek vám dal několik dobrých nápadů, které pomohou vašim žákům přistupovat s důvěrou.
online lekce matematiky 1-to-1 důvěryhodné školami a učiteli
každý týden učitelé matematiky třetího vesmírného učení podporují tisíce dětí základních škol s týdenními online lekcemi 1-to-1 a matematickými intervencemi. Od roku 2013 jsme pomohli více než 100 000 dětem stát se sebevědomějšími a schopnějšími matematiky. Zjistěte více nebo požádejte o osobní nabídku, abyste s námi mluvili o vašich potřebách a o tom, jak vám můžeme pomoci.
výuka na základní škole zaměřená na potřeby každého dítěte a pečlivě sledující Národní osnovy.