hjørner, ansigter og kanter kommer meget op i grundskolens geometri, når børn lærer om egenskaberne ved 3D-former. Her forklarer vi, hvad hver af disse betyder, og hvordan man beregner antallet af hjørner, ansigter og kanter til enhver form. Vi inkluderer også antallet af kanter, ansigter og hjørner af de mest almindelige former.
dette ordforråd introduceres i den nationale læseplan på År 2, og derfor kan følgende oplysninger bruges sammen med elever i grundskoleårene. Selv år 1 elever kan begynde at engagere sig i formernes egenskaber på denne måde, hvis du vil give dem et forspring!
Hvad er hjørner i figurer?
hjørner i figurer er de punkter, hvor to eller flere linjesegmenter eller kanter mødes (som et hjørne). Ental af hjørner er toppunkt. For eksempel har en terning 8 hjørner, og en kegle har et toppunkt.
hjørner kaldes undertiden hjørner, men når man beskæftiger sig med 2D-og 3D-figurer, foretrækkes ordet hjørner.
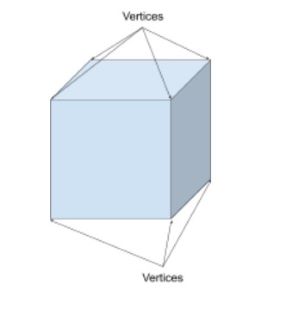
en terning har 8 hjørner. 7 er synlige her, og en er skjult.
Hvad er kanter?
kanter er de linjesegmenter, der forbinder et toppunkt til et andet, og er også hvor figurens ansigter mødes. Disse kan bruges til at beskrive 2D og 3D figurer.
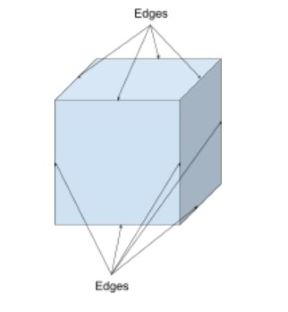
selvom mange former har lige linjer og lige kanter, er der former, der har buede kanter, såsom en halvkugle. En terning vil have 12 lige kanter som set nedenfor; 9 er synlige og 3 er skjult.

gratis 3D-figurer uafhængige Recap regneark
Hjælp dine År 2 (og ældre) elever med at revidere hjørner, ansigter og kanter med vores Gratis uafhængige Recap regneark.
Hvad er ansigter?
ansigter er den flade overflade af en solid form. For eksempel har en kuboid 6 ansigter. Når man tænker på 2D-og 3D-figurer, er det vigtigt at vide, at en 2D-form kun repræsenterer ansigtet på en 3D-form.
det er også vigtigt at vide, at da vores virkelighed er konstrueret i 3 dimensioner, er det umuligt at fysisk håndtere 2D-former, da vi er omgivet af 3-dimensionelle former. Derfor, hvis der i dit klasseværelse er en skuffe mærket ‘2d-figurer’, skal dette fjernes, da det lærer børn en misforståelse. Selvom et interaktivt koncept til klasseværelset, kan 2D-figurer kun eksistere som 2 dimensionelle tegninger.
du kan have både flade ansigter og buede ansigter, men jeg finder det nyttigt at henvise til buede ansigter som buede overflader, da det passer godt sammen med formens visuelle.
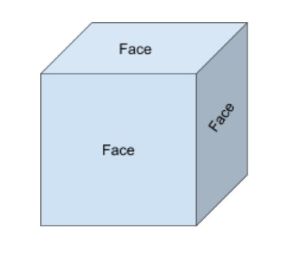
der er tre ansigter, der er synlige, og tre, der er skjult på terningen nedenfor.
hjørner, ansigter og kanter af almindelige 3D-former
hvor mange ansigter, kanter og hjørner har en kuboid?
en kuboid har 8 hjørner.
en kuboid har 12 kanter.
en kuboid har 6 ansigter.

hvor mange ansigter, kanter og hjørner har en cylinder?
en cylinder har 0 hjørner.
en cylinder har 2 kanter.
en cylinder har 2 flader og 1 buet overflade.

hvor mange ansigter, kanter og hjørner har en halvkugle?
en halvkugle har 0 hjørner.
en halvkugle har 1 buet kant.
en halvkugle har 1 ansigt og 1 buet overflade.

hvor mange ansigter, kanter og hjørner har en kegle?
en kegle har 1 toppunkt.
en kegle har 1 kant.
en halvkugle har 1 ansigt og 1 buet overflade.

hvor mange ansigter, kanter og hjørner har en tetraeder?
en tetraeder har 4 hjørner.
en tetraeder har 6 kanter.
en tetraeder har 4 ansigter.

hvor mange ansigter, kanter og hjørner har en kugle?
en kugle har 0 hjørner.
en tetraeder har 0 kanter.
en tetraeder har 1 buet overflade.

hvor mange ansigter, kanter og hjørner har et prisme?
et prisme er en fast genstand, geometrisk form eller polyhedron, hvor ansigterne i begge ender har samme form. Som sådan vil eleverne komme på tværs af mange typer prismer i hele deres skolegang. Almindelige inkluderer terninger, kuboider, trekantede prismer, femkantede prismer og sekskantede prismer.
| form | billedlig | ansigter | kanter | hjørner |
|---|---|---|---|---|
| trekantet prisme | 5 | 9 | 6 | |
| femkantet prisme | 7 | 15 | 10 | |
| sekskantet prisme | 8 | 18 | 12 | |
| Cube |
 |
6 | 8 | 12 |
| Cuboid |  |
6 | 8 | 12 |
hvornår lærer børn om hjørner, ansigter og kanter i folkeskolen?
børn skal formelt introduceres til ordforrådet for hjørner, ansigter og kanter i år 2, når de studerer geometri. Lærere kan dog vælge at introducere dette ordforråd Tidligere.
år 2 elever skal kunne:
- Identificer og beskriv egenskaberne for 3D-figurer, herunder antallet af kanter, hjørner og flader
den ikke-lovbestemte vejledning siger, at:
- eleverne håndterer og navngiver en lang række almindelige 2D-og 3D-former, herunder: kvadrilateraler og polygoner og kuboider, prismer og kegler og identificerer egenskaberne for hver form (for eksempel antal sider, antal ansigter). Eleverne identificerer, sammenligner og sorterer figurer ud fra deres egenskaber og bruger ordforråd præcist, såsom sider, kanter, hjørner og ansigter.
fra dette tidspunkt henviser den nationale læseplan ikke eksplicit til hjørner, ansigter og kanter igen, så lærere i andre årgrupper bliver nødt til at fortsætte med at bruge dette ordforråd, når man ser på form
hvordan forholder hjørner, ansigter og kanter sig til andre områder af matematik?
studerende vil bruge viden om hjørner, ansigter og kanter, når man ser på 2d-figurer såvel som 3D-figurer. At vide, hvilke kanter der er, og identificere dem på sammensatte former er afgørende for at finde omkredsen og arealet af 2D sammensatte former. Det er et vigtigt fundament for senere år, når man beskæftiger sig med forskellige matematiske sætninger, såsom grafteori og paraboler.
hvordan forholder hjørner, ansigter og kanter sig til det virkelige liv?
ethvert objekt i det virkelige liv har hjørner, ansigter og kanter. For eksempel er en krystal en oktaeder – den har otte ansigter, tolv kanter og seks hjørner. At kende disse egenskaber til forskellige tredimensionelle former lægger grundlaget for forskellige industrier såsom arkitektur, interiørdesign, teknik og mere.
hjørner, ansigter og kanter eksempel spørgsmål
1. Forklar, hvad et toppunkt er.
(svar: et toppunkt er hvor to linjer mødes)
2. Hvor mange kanter har et trekantet prisme?
(svar: 9)
3. Hvor mange hjørner har en kegle?
(svar: 1 toppunkt)
4. Hvor mange ansigter har en kuboid? Hvad er 2D-formerne på disse ansigter?
(svar: 6 ansigter. De kan have 2 firkantede ansigter og 4 rektangulære ansigter eller kun 6 rektangulære ansigter.)
5. For alle de fælles prismer (terninger, cuboids, trekantede prismer, femkantede prismer og sekskantede prismer) tilføje ansigter og knudepunkter sammen og trække kanterne. Hvad bemærker du om svarene?
(svar: svaret er altid 2. Dette er kendt som Eulers formel (antal hjørner – antal kanter + antal ansigter = 2)
spekulerer du på, hvordan du forklarer andre vigtige matematiske ordforråd til dine børn? Tjek vores primære Matematikordbog, eller prøv disse:
- Hvad er Maths Mastery?
- Hvad er 2D-figurer?
- Hvad er 3D-figurer?
du kan finde masser af geometri lektionsplaner og udskrivbare regneark til grundskoleelever på den tredje Space Learning Maths Hub.
Online 1-til-1 matematiklektioner, som skoler og lærere har tillid til
hver uge Third Space Learning ‘ s matematikspecialistlærere støtter tusinder af grundskolebørn med ugentlige online 1-til-1-lektioner og matematikinterventioner. Siden 2013 har vi hjulpet over 100.000 børn med at blive mere selvsikre, dygtige matematikere. Få mere at vide, eller bed om et personligt tilbud for at tale med os om dine behov, og hvordan vi kan hjælpe.
vores online undervisning for matematik program giver hvert barn med deres egen professionelle en til en matematik tutor