i denne vejledning forklarer jeg, hvad standardfejlformlen er, og hvordan man bruger den til at udarbejde standardfejlen ved hjælp af et eksempel.
hvad er standardfejlen?
standardfejlen (SE), undertiden benævnt standardfejlen for gennemsnittet (SEM), er en statistik, der svarer til standardafvigelsen for en prøveudtagningsfordeling i forhold til middelværdien. Men hvad er det egentlig?
sig, at du er interesseret i den gennemsnitlige alder, som folk i Storbritannien er diagnosticeret med. Det er ikke muligt at bestemme dette for alle i Storbritannien, derfor tager forskere en stikprøvepopulation for at generalisere et samlet tal. For eksempel kan 10.000 Britiske mennesker med sygdommen analyseres og vil blive brugt til at generere gennemsnitsalderen for diagnosen. Hvis du gør dette på en tilfældig prøve på 5.000 patienter, kan du få en gennemsnitlig diagnosealder på 61,5 år. Men hvis du foretager prøveanalysen på en separat tilfældig prøve på 10.000 andre patienter, kan du få en gennemsnitlig alder på 62,3 år. Lad os sige, hypotetisk set selvfølgelig, at hvis du var i stand til at analysere alle de mennesker i Storbritannien, der har sygdommen for at få det faktiske tal, kan du ende med 64,3 år. Du kan bemærke, at tallene opnået fra prøvepopulationerne (61,5 og 62,3 år) adskiller sig fra det faktiske tal (64,3 år). Denne variation i middelværdier forventes, og når du øger antallet af personer i din prøvepopulation, får du en værdi, der er tættere på det faktiske tal. Dette er præcis, hvad standardfejlen repræsenterer. Standardfejlen betyder denne variation i middelværdierne mellem prøvepopulationerne.
For yderligere læsning foreslår jeg, at du læser den korte Statistiknote af professorer Douglas Altman og Martin Bland offentliggjort i British Medical Journal. Det er en nyttig indsigt i, hvad standardfejlen er, og hvad forskellen med standardafvigelsen er.
standardfejlformlen
for at beregne standardfejlen skal du have to oplysninger: standardafvigelsen og antallet af prøver i datasættet. Standardfejlen beregnes ved at dividere standardafvigelsen med kvadratroden af antallet af prøver.
her er den fulde annoterede standardfejlformel:
eksempel
for at forstå standardfejlformlen bedre kan det hjælpe med at gennemgå et eksempel. Sig, at vi har en befolkning på 80 mennesker, og vi er interesserede i deres højde. Vi måler deres højde og Beregner standardafvigelsen som 30,6 cm. Vi skal nu tilslutte disse værdier til vores ligning:
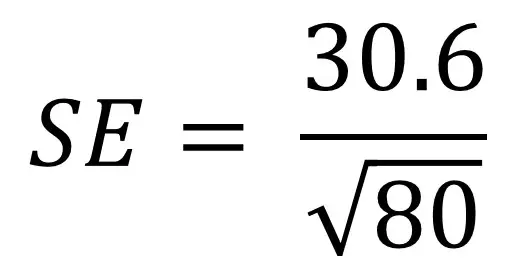 hvis du er ubehagelig med at indtaste ligninger i regnemaskiner, kan du nedbryde formlen i håndterbare bidder. Her er de trin, du kan tage.
hvis du er ubehagelig med at indtaste ligninger i regnemaskiner, kan du nedbryde formlen i håndterbare bidder. Her er de trin, du kan tage.
- Beregn først kvadratroden af antallet af prøver (n). I dette tilfælde er n 80. Kvadratroden af 80 er 8,94.
- divider derefter standardafvigelsen (30.6) med kvadratroden på 80 (8.94). Dette giver en værdi på 3,42.
- derfor er standardfejlen i vores befolkning for højde 3,42 cm.