Division I nøglefase 2 udgør den sidste del af ‘fire operationer’ – de fire grundlæggende matematiske begreber, som eleverne skal kende. Denne blog hjælper dig med at sikre, at alle dine elever, fra år 3 til år 6, kan nærme sig division med den tillid, de har brug for for at få succes.
Division I KS2 matematik bygger på, hvad der er blevet lært på KS1. Ved udgangen af Y2 studerende på den forventede standard vil være i stand til at ‘ huske og bruge multiplikation og division fakta for 2, 5 og 10 gangetabeller, herunder anerkendelse ulige og lige tal.’
for lærere i år 3 er det altid en god ide at sikre, at de studerende kender disse meget godt. Med det, jeg mener ikke blot, at de kan papegøje divisionsfakta hos dig, men de forstår virkelig, hvordan man repræsenterer disse fakta både med konkrete repræsentationer, verbale forklaringer og gennem andre billedmetoder.
studerende, der ikke er i stand til at gøre dette, men alligevel er i stand til verbalt at fortælle dig divisionsfakta, har en meget lav forståelse af division, og for at de kan komme videre til vanskeligere problemløsningsaktiviteter, er uddybning af deres konceptuelle forståelse af division et must i år 3.
den nationale læseplan placerer division inden for samme sektion som multiplikation i år 3-5 og placerer den inden for et afsnit kaldet ‘fire operationer’ i år 6. De dele, der er taget fra den nationale læseplan, vedrører kun dem, der specifikt nævner division. De andre elementer i disse sektioner kan findes i bloggen om multiplikation eller addition og subtraktion, hvor det er relevant.
Hvad Er Division?
Division er en af de fire operationer – de fire grundlæggende matematiske begreber, som eleverne skal kende – sammen med addition og subtraktion og multiplikation.
hvor multiplikation kombinerer et tal flere gange, er division det modsatte: at finde ud af, hvor mange gange et tal er indeholdt i et andet. For eksempel spørger dividere 10 med 2, hvor mange gange 2 er indeholdt i 10.

fra Third Space Learning ‘ s online matematikinterventioner.
undervisning Division KS2-teorien
Division er den inverse af multiplikation. Som med multiplikationsbloggen indeholder undervisningen i division tre underliggende strukturer, som, når de kombineres med divisionsfakta og konceptuel forståelse, giver de studerende den bedste mulighed for at få succes, når de løser problemer relateret til division.
de tre strukturer er deling, gruppering og skalering. Selvom der ikke er tid nok til at udforske disse i dybden, vil det følgende kun være en kort introduktion til dem.
deling og gruppering er det omvendte af multiplikation som gentagen tilføjelse. Deling er et strukturelt koncept, der introduceres i KS1 og tidligere, hvor, som navnet antyder, et beløb deles i lige store grupper.
for eksempel deles 12 æbler blandt 3 studerende. Hvor mange æbler får hver elev? Her kender vi hele beløbet (12 æbler) og afgørende, Vi ved, hvordan det beløb, vi vil dele i (3). Afhængigt af hvor eleverne er på deres matematiske rejse, kan de gentagne gange trække med et tal (1, 2, 3 eller 4) fra mængden i tre bunker, der repræsenterer de tre studerende.
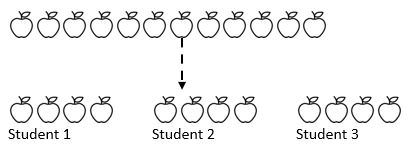
som vi kan se af ovenstående, er hele beløbet blevet delt i tre lige store grupper.
gruppering svarer til deling, men det, vi ved, er lidt anderledes sammenlignet med deling. I delingsstrukturen kender vi mængden af grupper, som delingen vil finde sted. I grupperingsstrukturen kender vi beløbet i hver gruppe, men ikke antallet af faktiske grupper, der er.
for eksempel deles 12 æbler i grupper på 4. Hvor mange grupper vil der være? Selvom dette spørgsmål meget ligner det ovenstående, påtager det sig nu grupperingsstrukturen, da vi ved, hvor mange der vil gå ind i hver gruppe, men ikke længere ved, hvor mange grupper der nu vil være.
da vi ved, at der er 4 i hver gruppe, kan vi gruppere 4 æbler, indtil vi har dækket alle 12 for at se, at der er 3 grupper.
den endelige struktur af division er skalering. Mens vi i multiplikation opskalerede en værdi, skalerer divisionsstrukturen ned. For eksempel har Shannen 6 penne og Jen har 3 gange så færre. Hvor mange penne har Jen?
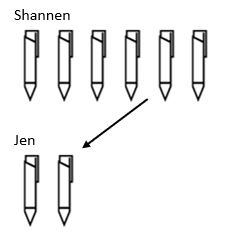
her kan vi se, at for at finde den samlede mængde penne, som Jen har, måtte vi tage det beløb, som Shannen havde, og reducere det med en skalafaktor på 3, så Jen ender med 2 penne.
fra erfaring er dette den sværeste opdelingsstruktur for studerende at forstå og forstå og er en, der skal revideres i forbindelse med skalering som multiplikation, da dette er en afgørende færdighed, når man konverterer målinger og valutaer fra et større beløb til et mindre beløb. F. eks. kilometer til miles.
Divisionsår 3
i den nationale læseplan for matematik i England er der for hvert område af matematik skitseret både et lovbestemt element og et ikke-lovbestemt element. Det lovbestemte element er som følger:
- Husk og brug multiplikation og division fakta for 3, 4 og 8 multiplikationstabeller
- Skriv og beregne matematiske udsagn for multiplikation og division ved hjælp af de multiplikationstabeller, de kender, herunder for tocifrede tal gange etcifrede tal, ved hjælp af mentale og fremskridt til formelle skriftlige metoder
- Løs problemer, herunder manglende talproblemer, der involverer multiplikation og division, herunder positive heltalskaleringsproblemer og korrespondanceproblemer, hvor n objekter er forbundet til m objekter.
ikke-lovpligtige noter og vejledning:
- eleverne udvikler effektive mentale metoder, for eksempel ved hjælp af kommutativitet og associativitet (for eksempel, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) og multiplikation og division fakta (for eksempel ved hjælp af 3 × 2 = 6, 6 ÷ 3 = 2 og 2 = 6 3) for at udlede relaterede fakta (for eksempel, 30 × 2 = 60, 60 ÷ 3 = 20 20 = 60 3).
- eleverne udvikler pålidelige skriftlige metoder til multiplikation og division, begyndende med beregninger af tocifrede tal med etcifrede tal og fremskridt til de formelle skriftlige metoder til kort multiplikation og division.
- eleverne løser simple problemer i sammenhænge og beslutter, hvilken af de fire operationer der skal bruges, og hvorfor. Disse inkluderer måle-og skaleringskontekster (for eksempel fire gange så høje, otte gange så lange osv.) og korrespondanceproblemer, hvor m-objekter er forbundet med n-objekter (for eksempel 3 hatte og 4 frakker, hvor mange forskellige tøj?; 12 slik deles ligeligt mellem 4 børn; 4 kager deles ligeligt mellem 8 børn).
Divisionsaktiviteter år 3
dette dækker ikke en lektion i sig selv, men giver en guide til, hvordan opdeling kan undervises med en vis konceptuel forståelse på dette stadium. En forudsætning for dette ville være undervisningen i relaterede multiplikationsfakta først, før man underviser i nogen relateret opdeling.
når man tænker på strukturer, er det bedst på denne del af elevernes læringsrejse at holde fast i gruppering og deling. For de følgende eksempler, vi vil se på at udvikle elevernes forståelse for at dividere med 4. Det vil følge den konkrete-billedlige-abstrakte tilgang.
det er ofte elevernes forståelse af tal, der kan begrænse deres fremskridt i division. Især når det kommer til gruppering og deling, når de kun tager en væk kontinuerligt fra helheden.
fra starten af undervisningsafdelingen skal lærerne læne sig på, hvad eleverne allerede ved om lige tal og andre talfakta for at udvikle eleverne til at tælle i hvilket antal der måtte være passende.
tællere kan bruges til at demonstrere relaterede divisionsfakta, da eleverne vil have brugt afhandlinger, når de bygger deres konceptuelle forståelse af multiplikation. Spørgsmål som: ‘hvor mange grupper på 4 er der?’og’ hvor mange er der i hver gruppe?’bør stilles, og svarene skal vedrøre, hvordan dette viser opdeling.
lærer: hvor mange tællere er der?
Barn: Fire
Lærer: God. Dette er en gruppe på fire. Hvor mange grupper på fire er der?
Barn: En
Lærer: Fremragende. Vi har fire tællere i en gruppe. Vi har grupperet fire tællere i en gruppe. Hvad har vi gjort?
barn: grupperet fire tællere i en gruppe.
Lærer: Strålende. Når vi grupperer fire tællere i en gruppe, har vi foretaget den matematiske beregning af fire divideret med en. Hvilken beregning gjorde vi?
barn: fire divideret med en.
lærer: og når vi løser fire divideret med en, er svaret fire, fordi vi har lavet en gruppe, der har fire elementer i den. Fire divideret med en er fire. Hvad er fire divideret med en?
barn: Fire divideret med en er fire.
Lærer: fremragende
du kan se, hvordan det ville blive gentaget for følgende:
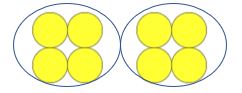
lærer: hvor mange tællere er der?
barn: otte
lærer: godt, dette er en gruppe på fire. Hvor mange grupper på fire er der?
Barn: To
Lærer: Fremragende. Vi har fire tællere i en gruppe. Vi har grupperet fire tællere i to grupper. Hvad har vi gjort?
barn: grupperet fire tællere i to grupper.
Lærer: Strålende. Når vi grupperer fire tællere i to grupper, har vi foretaget den matematiske beregning af otte divideret med to. Hvilken beregning gjorde vi?
barn: otte divideret med to.
lærer: og når vi løser otte divideret med to, er svaret fire, fordi vi har lavet to grupper, der har fire elementer i det. Otte divideret med to er fire. Hvad er otte divideret med to?
barn: otte divideret med to er fire.
Lærer: fremragende
når eleverne er begyndt at få tillid til dette, kan vi gå videre til andre modeller såsom Cuisenaire stænger.

her er hele beløbet repræsenteret i det øverste tog, og den lilla stang (som i dette tilfælde repræsenterer 4, og hvis du har læst andre blogs i denne serie forhåbentlig vil du vide, hvor meget af en advokat jeg er til deres brug i klasseværelset, og så studerende vil være opmærksomme på dens værdi inden da) bruges til at vise, hvor mange grupper på 4 der kan gå ind i det samlede beløb.
studerende kan derefter gå videre til at tegne scenarier læst af læreren. Eksempel. Der er 24 knapper, og de skal grupperes i 4. Hvor mange grupper er der? Studerende kunne tegne disse knapper og gruppere dem i 4 osv.
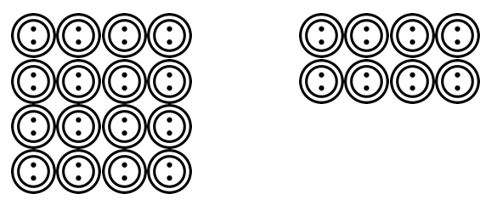
når eleverne har vænnet sig til at kunne visualisere disse gruppering eller deling division scenarier i en række sammenhænge, så kan de gå videre til mere abstrakte repræsentationer ved hjælp af matematiske symboler.

3 Long Division regneark i årevis 3-6
få dine elever forberedt til lang division i hele KS2 med disse long division regneark.
Division ord problemer År 3
ord problemer i år 3 vil almindeligvis bruge gruppering eller deling struktur.
der er 40 kager og 10 studerende. Hvor mange kager får hver elev?
da vi ved, hvor mange grupper der er (10), skal vi udarbejde beløbet pr. Studerende forventes at bruge deres viden om 4-tidstabellen til at finde ud af dette og få svaret 4.
Division: Ræsonnement og problemløsning år 3
til ræsonnement og problemløsning er en god aktivitet, jeg finder, at matche et ordproblem til en beregning. For eksempel:
Match de ordproblemer, der løses ved at kende 20 divideret med 4.
- der er 20 blyanter, og de skal placeres i pakker med 5. Hvor mange i hver pakke?
- der var 20 blyanter og derefter en studerende bringer i 4 mere. Hvor mange blyanter er der nu?
- der er 20 blyanter, og de skal placeres i pakker med 4. Hvor mange i hver pakke?
- der var 20 blyanter, og derefter forsvandt 4. Hvor mange blyanter er der nu?
at få eleverne til at skrive ned deres forklaringer til hvert spørgsmål er nyttigt, da det giver mulighed for at se deres tænkning. Spørgsmålene er valgt omhyggeligt, så tallene i hvert spørgsmål vedrører tallene på spørgsmålet, så eleverne stoler på deres matematiske færdigheder for at udlede det rigtige svar.
Divisionsår 4
i den nationale læseplan for matematik i England er der for hvert område af matematik skitseret både et lovbestemt element og et ikke-lovbestemt element. Det lovbestemte element er som følger:
- Recall multiplikation og division fakta for multiplikationstabeller op til 12 liter 12
- brug stedværdi, kendte og afledte fakta til at multiplicere og opdele mentalt, herunder: multiplicere med 0 og 1; dividere med 1; multiplicere tre tal
ikke-lovpligtige noter og vejledning:
- eleverne fortsætter med at øve sig på at huske og bruge multiplikationstabeller og relaterede opdelingsfakta for at hjælpe flydende.
- eleverne praktiserer mentale metoder og udvider dette til trecifrede tal for at udlede fakta (for eksempel kan 600 3 = 200 stamme fra 2 gange 3 = 6).
- eleverne praktiserer at blive flydende i den formelle skriftlige metode til kort multiplikation og kort opdeling med nøjagtige svar
- eleverne løser totrinsproblemer i sammenhænge, vælger den passende operation, arbejder med stadig hårdere tal. Dette bør omfatte korrespondance spørgsmål såsom antallet af valg af et måltid på en menu, eller tre kager deles ligeligt mellem 10 børn.
Division Lesson Ideas år 4
til denne lektion vil jeg se på, hvordan du kan begynde at undervise i kort division ved hjælp af manipulativer ved siden af det.
sig, at vi skal undervise eleverne kort division for spørgsmålet 168 divideret med 12.
vi ville normalt skrive dette i det, der almindeligvis omtales som busstoppested. Men hvad der er interessant er, at forskellige steder i verden skriver det anderledes.
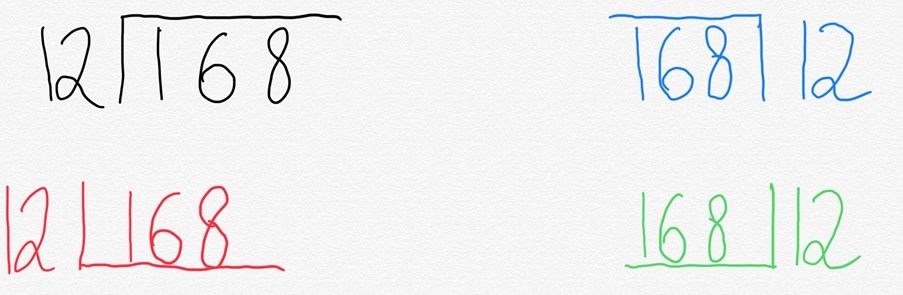
årsagen til dette er ret simpelt. Hvad ‘busstoppestedet’ faktisk repræsenterer er en forkortet måde at repræsentere et rektangel på.
når vi underviser i Formel kort opdeling, siger vi faktisk, at du skal forestille dig et rektangel, hvor bredden er 12. Det samlede areal af rektanglet er 168, og vi forsøger at finde den manglende længde på tværs af toppen. Så hvordan viser vi dette ved hjælp af manipulativer? Dienes blokke er et nyttigt værktøj til dette.
vi ved, at det samlede beløb er 168. Så vi er nødt til at samle 168 værd af diener ved hjælp af de mindste mængder af blokke muligt. Dette er vist nedenfor.
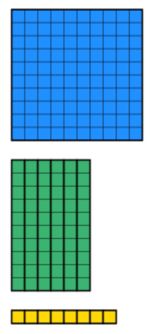
når vi ser tilbage på spørgsmålet, ved vi, at bredden er 12. Det betyder, at vi nu skal manipulere blokkene, så vi får en bredde på 12. Bemærk, at rektanglet skal være solidt og kan ikke have manglende dele. For eksempel ville nedenstående ikke være tilladt på trods af at der er 12 enheder, der går ned i bredden.
i stedet kan eleverne rotere to 10s blokke for at få følgende. Bemærk, hvordan der er 12 i hver kolonne, og det er et solidt objekt.
den sidste del, som eleverne skal gøre, er at bruge de resterende blokke til at oprette et solgt rektangel, mens bredden holdes 12. Dette kan tage lidt tid, men med praksis bliver eleverne hurtigere. Efter nogen tid vil eleverne producere dette:
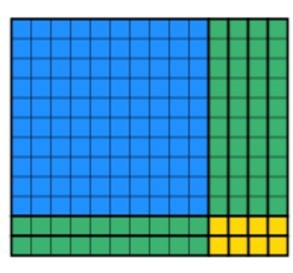
vi kan se, at alle 168 værd af blokke er brugt op, og at bredden stadig er 12. For at finde svaret skal eleverne tælle længden, som i dette tilfælde er 14. Jeg har overlejret begge metoder nedenfor, så du kan se, hvordan de supplerer hinanden nedenfor.
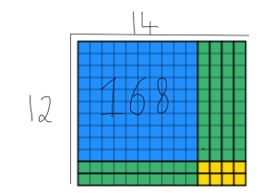
dette er en nyttig strategi til at undervise studerende i år 4, da der er massive konsekvenser på andre områder af læseplanen, der allerede er belyst for studerende.
selvom de måske ikke genkender det endnu, ved at undervise i kort opdeling som denne, er de allerede blevet introduceret til omkreds og område – tænk på, hvor meget undervisningstid der kan spares, når denne forbindelse oprettes. Ikke kun det, men i sekundær overfører denne tilgang til algebraisk tænkning.
Divisionsordproblemer år 4
studerende forventes at trække på deres viden om stedværdi for at løse divisionsbaserede problemer, og så ville et passende ordproblem være.
en frugtplantage dyrkede 4.800 æbler i en sæson. De placeres i pakker med 4, inden de går på markedet. Hvor mange pakker er der?
her skal eleverne bruge det faktum, at 4 gange 12 = 48 og som 4.800 er hundrede gange mere end 48, 12 skal også ganges med 100 for at få 1.200
Division: Ræsonnement og problemløsning år 4
er det altid, nogle gange eller aldrig sandt, at summen af tre lige tal kan deles med 4?
dette spørgsmål giver eleverne rig mulighed for at eksperimentere inden for parametrene for spørgsmålet. Studerende, der har brug for mere støtte, kan se på sing digit even numbers, og studerende kan gå op til det, de føler sig godt tilpas med.
med åbne spørgsmål som dette er det godt at stille et minimumskrav til, hvor mange forsøg eleverne skal gøre ellers vælger de ofte at gøre det absolutte minimum.
svaret på dette spørgsmål er nogle gange.
et hurtigt ‘trick’ for at vide, om et tal kan deles, er at se på de sidste 2 cifre i tallet og se, om de kan deles med 4. For eksempel, hvis et barn fandt summen af 34, 36 og 38 og fik 108, ved jeg som lærer, at dette tal kan deles med 4, da de sidste to cifre (08) udgør 8 og kan deles med 4. Hvis et barn valgte 34, 36 og 48 for at få 118, ved jeg, at dette ikke kan deles med 4, Da 18 – de sidste to cifre på 118 – ikke kan deles med 4.
Divisionsår 5
i den nationale læseplan for matematik i England er der for hvert område af matematik skitseret både et lovbestemt element og et ikke-lovbestemt element. Det lovbestemte element er som følger:
- Multiplicer og divider tal mentalt ved at trække på kendte fakta
- Opdel tal op til 4 cifre med et etcifret tal ved hjælp af den formelle skriftlige metode til kort opdeling og fortolke remainders passende for konteksten
- Multiplicer og divider hele tal og dem, der involverer decimaler med 10, 100 og 1000
- Løs problemer, der involverer multiplikation og division, herunder brug af deres viden om faktorer og multipler, firkanter og terninger
- løse problemer med addition, subtraktion, multiplikation og division og en kombination af disse, herunder forståelse af betydningen af lighedstegnet
- løser problemer med multiplikation og division, herunder skalering med enkle fraktioner og problemer med enkle satser.
ikke-lovpligtige noter og vejledning:
- elever fortolker ikke-heltalssvar på division ved at udtrykke resultater på forskellige måder i henhold til konteksten, inklusive med rester, som brøker, som decimaler eller ved afrunding (for eksempel 98 liter 4 = = 24 r 2 = 24 = 24,5 liter 25).
- elever bruger multiplikation og opdeling som inverser til at understøtte introduktionen af forholdet i år 6, for eksempel ved at multiplicere og dividere med kræfter på 10 i skalategninger eller ved at multiplicere og dividere med kræfter på 1.000 i konvertering mellem enheder som kilometer og meter.
Divisionsaktiviteter år 5
Division i år 5 skrider frem ved brug af rester i svar. Til denne lektion vil jeg se på en anden brug manipulativer, som lærere kan bruge til at undervise i 4-til-1-cifret division.
hvis spørgsmålet var 5.642 divideret med 4, kunne vi repræsentere dette ved hjælp af et stedværdidiagram og stedværdi tællere, som vi kan se nedenfor.
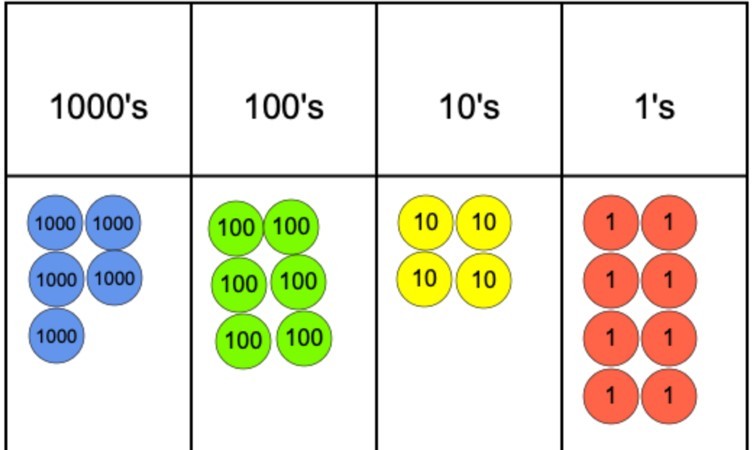
det næste skridt ville være at begynde at gruppere tællerne i 4, da dette er vores divisor. Men som det kan ses, kommer vi hurtigt til et problem i kolonnen 1000, da vi er i stand til at gruppere 4 af tællerne, men så kan vi ikke gruppere den resterende tæller i en gruppe på 4.
for at bekæmpe dette problem kan 1000-tælleren, der ikke er grupperet, udveksles til ti 100-tællere. Disse kan derefter grupperes i grupper på 4, og dette kan ske uden at der er nogen 100s tællere tilbage. Derfra er det et simpelt tilfælde at flytte til 10 ‘ erne og endelig dem.
da der er ni 1s-tællere, kan vi gruppere 8 af dem i 2 grupper og 4 og hævde, at der er en tilbage*. For at finde svaret er alt, hvad der kræves, at tælle antallet af grupper, der er foretaget i hver stedværdi, og bruge disse til at skrive cifrene for at oprette det endelige svar. I dette tilfælde ville svaret være 1.412 resten 1.
*når du kigger på decimaler, kan du bytte den resterende 1s tæller til ti 0,1 tællere og fortsætte divisionen som beskrevet ovenfor. Studerende, der er fortrolige med denne model, er nyttige, da det kan hjælpe med at afmystificere opdeling med decimaler, som studerende kan kæmpe med. Dette hjælper dem med at se, at det er en fortsættelse af en proces, som de allerede er bekendt med snarere end noget nyt.
Divisionsproblemer år 5
når de deler sig i år 5, vil de studerende støde på scenarier, hvor de bliver nødt til at afrunde deres svar for at Svaret giver mening i sammenhængen. Et passende spørgsmål, der demonstrerer dette, ville være noget som følgende:
en skole planlægger et socialt distanceret diskotek, hvor de planlægger at tilbyde 250 ml juice til hver elev. De kan købe 2 liter flasker juice. De forventer, at 33 studerende ankommer, så de ved, at de vil give 8,25 liter juice. Hvor mange flasker juice skal de købe?
et fælles svar er, at eleverne vil sige 4 og en fjerdedel. Imidlertid, da du ikke kan købe en fjerdedel af en flaske, i dette tilfælde ville det rigtige svar være 5 flasker juice ville være nødvendigt for at sikre, at alle studerende kunne deltage.
Division: ræsonnement og problemløsning år 5
som nævnt ovenfor vil studerende i år 5 støde på scenarier inden for division, hvor de skal vælge, om et svar skal afrundes op eller ned. For eksempel, når et spørgsmål beder eleverne om at finde ud af, hvor mange busser der er brug for til en skole en tur.
at få eleverne til at skabe deres egne problemer ved hjælp af en række forudsat kontekst kan være en virkelig udfordrende aktivitet, der får eleverne til at tænke matematisk om kontekst og division.
studerende kan derefter bytte disse spørgsmål, de har oprettet med en partner, og derefter gå i gang med at løse dem og tjekke med den originale spørgsmålsskaber, hvis de har det rigtige svar.
Divisionsår 6
i den nationale læseplan for matematik i England er der for hvert område af matematik skitseret både et lovbestemt element og et ikke-lovbestemt element. Det lovbestemte element er som følger:
- opdel tal op til 4 cifre med et tocifret heltal ved hjælp af den formelle skriftlige metode til lang opdeling, og fortolke rester som heltalrester, brøker eller ved afrunding, alt efter hvad der er relevant for konteksten
- opdel tal op til 4 cifre med et tocifret tal ved hjælp af den formelle skriftlige metode til kort opdeling, hvor det er relevant, tolkning af rester i henhold til konteksten
- udfør mentale beregninger, herunder med blandede operationer og store tal
- identificer fælles faktorer, fælles multipla og primtal
- brug deres viden om rækkefølgen af operationer til at udføre beregninger, der involverer de fire operationer
ikke-lovpligtige noter og vejledning:
- Løs problemer med addition, subtraktion, multiplikation og division
- brug estimering til at kontrollere svar på beregninger og bestemme i forbindelse med et problem en passende grad af nøjagtighed.
Division Lesson Ideas år 6
Sophie Bartlett (@_MissieBee) har oprettet en fremragende blog her (link til Sophies blog om undervisning i lang division), der beskriver, hvordan hun ville undervise i lang division i et år 6 klasse. Da long division er den eneste nye læring om division i år 6, er dette en ideel måde at introducere proceduren for long division.
Divisionsspørgsmål år 6
et typisk divisionsordproblem, som en studerende på år 6 ville støde på, ville være:
en skole rejste 3.146 fra et bagesalg. 104 forældre deltog i arrangementet. Hvis alle forældre brugte lige mange penge,hvor meget brugte hver forælder?
her forventes studerende at bruge long division-metoden til at løse dette spørgsmål for at få svaret på 30.25.
Division: ræsonnement og problemløsning år 6
med noget proceduremæssigt som lang division er en god ræsonnementsaktivitet at få eleverne til at finde fejl. Disse ressourcer giver en stor bank af sådanne aktiviteter. Som vi kan se af nedenstående spørgsmål, har eleverne gjort alt det hårde arbejde, men en skødesløs fejl ved at tælle grupperne på 59 betyder, at barnet troede 59 gange 7 var 472 og ikke 59 gange 8.
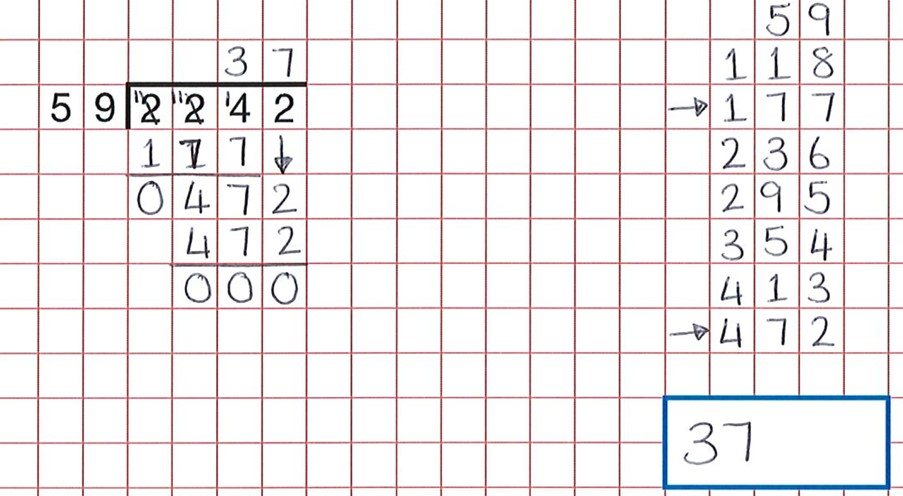
det rigtige svar ville have været 38.
Division er et vigtigt matematikemne, ikke kun hos KS2, men i matematik som helhed. Forhåbentlig har dette indlæg givet dig nogle gode ideer til at hjælpe dine elever med at nærme sig det med tillid.
Online 1-til-1 matematiklektioner, som skoler og lærere har tillid til
hver uge Third Space Learning ‘ s matematikspecialistlærere støtter tusinder af grundskolebørn med ugentlige online 1-til-1-lektioner og matematikinterventioner. Siden 2013 har vi hjulpet over 100.000 børn med at blive mere selvsikre, dygtige matematikere. Få mere at vide, eller bed om et personligt tilbud for at tale med os om dine behov, og hvordan vi kan hjælpe.
grundskoleundervisning målrettet mod hvert barns behov og nøje følge den nationale læseplan.