Teaching Division KS2: Ein Leitfaden für Grundschullehrer

Die Division in Key Stage 2 bildet den letzten Teil der ‚Vier Operationen‘ – die vier mathematischen Kernkonzepte, die Schüler kennen sollten. Dieser Blog wird Ihnen helfen, sicherzustellen, dass alle Ihre Schüler, von Jahr 3 bis Jahr 6, können sich der Division mit dem Vertrauen nähern, das sie brauchen, um erfolgreich zu sein.

Die Division in KS2 maths baut auf dem auf, was in KS1 gelernt wurde. Bis zum Ende von Y2 können die Schüler des erwarteten Standards Multiplikations- und Divisionsfakten für die 2, 5 und 10 Multiplikationstabellen abrufen und verwenden, einschließlich der Erkennung ungerader und gerader Zahlen.‘

Für Lehrer in der 3. Klasse ist es immer eine gute Idee, sicherzustellen, dass die Schüler diese sehr gut kennen. Damit meine ich nicht nur, dass sie die wahren Tatsachen auf Sie abbilden können, sondern sie verstehen es wirklich, diese Tatsachen sowohl mit konkreten Darstellungen, verbalen Erklärungen als auch durch andere bildliche Methoden darzustellen.

Studenten, die nicht in der Lage sind, dies zu tun, aber in der Lage sind, Ihnen die Fakten der Division mündlich mitzuteilen, haben ein sehr flaches Verständnis der Division und damit sie zu schwierigeren Problemlösungsaktivitäten übergehen können, ist die Vertiefung ihres konzeptionellen Verständnisses der Division ein Muss im Jahr 3.

Der nationale Lehrplan stellt die Division in den gleichen Abschnitt wie die Multiplikation für die Jahre 3-5 und platziert sie in einem Abschnitt namens ‚Four Operations‘ im Jahr 6. Die Teile aus dem Nationalen Lehrplan beziehen sich nur auf diejenigen, die die Teilung ausdrücklich erwähnen. Die anderen Elemente dieser Abschnitte finden Sie gegebenenfalls im Blog über Multiplikation oder Addition und Subtraktion.

Was ist Division?

Division ist neben Addition und Subtraktion und Multiplikation eine der vier Operationen – die vier mathematischen Kernkonzepte, die Schüler kennen sollten.

Wo Multiplikation eine Zahl mehrmals kombiniert, ist Division das Gegenteil: Herauszufinden, wie oft eine Zahl in einer anderen enthalten ist. Wenn Sie beispielsweise 10 durch 2 dividieren, werden Sie gefragt, wie oft 2 in 10 enthalten ist.

Division und Multiplikation sind Inverse voneinander, wie in dieser Folie
von Third Space Learning’s online Maths interventions gezeigt.

Teaching Division KS2 – Die Theorie

Division ist die Umkehrung der Multiplikation. Wie beim Multiplikationsprinzip enthält der Divisionsunterricht drei zugrunde liegende Strukturen, die in Verbindung mit Divisionsfakten und konzeptionellem Verständnis den Schülern die beste Gelegenheit bieten, bei der Lösung von Divisionsproblemen erfolgreich zu sein.

Die drei Strukturen teilen, gruppieren und skalieren. Es bleibt zwar nicht genug Zeit, um diese eingehend zu untersuchen, aber was folgt, ist nur eine kurze Einführung in sie.

Teilen und Gruppieren sind die Umkehrung der Multiplikation als wiederholte Addition. Sharing ist ein strukturelles Konzept, das in KS1 und früher eingeführt wird, wo, wie der Name schon sagt, ein Betrag in gleiche Gruppen aufgeteilt wird.

Zum Beispiel werden 12 Äpfel von 3 Schülern geteilt. Wie viele Äpfel bekommt jeder Schüler? Hier kennen wir den gesamten Betrag (12 Äpfel) und vor allem wissen wir, wie viel wir in (3) teilen werden. Je nachdem, wo sich die Schüler auf ihrer mathematischen Reise befinden, können sie wiederholt eine Zahl (1, 2, 3 oder 4) vom Betrag in drei Stapel subtrahieren, die die drei Schüler darstellen.

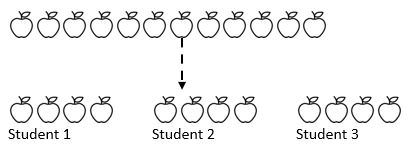
Wie wir oben sehen können, wurde der gesamte Betrag in drei gleiche Gruppen aufgeteilt.

Gruppierung ähnelt dem Teilen, aber was wir wissen, unterscheidet sich geringfügig vom Teilen. In der Freigabestruktur kennen wir die Anzahl der Gruppen, in denen die Freigabe stattfinden wird. In der Gruppierungsstruktur kennen wir den Betrag in jeder Gruppe, aber nicht die Anzahl der tatsächlich vorhandenen Gruppen.

Zum Beispiel werden 12 Äpfel in Gruppen von 4 geteilt. Wie viele Gruppen wird es geben? Während diese Frage der obigen sehr ähnlich ist, nimmt sie jetzt die Gruppierungsstruktur an, da wir wissen, wie viele in jede Gruppe gehen werden, aber nicht mehr wissen, wie viele Gruppen es jetzt geben wird.

Da wir wissen, dass es in jeder Gruppe 4 gibt, können wir 4 Äpfel gruppieren, bis wir alle 12 abgedeckt haben, um zu sehen, dass es 3 Gruppen gibt.

Die endgültige Struktur der Division ist Skalierung. Während wir bei der Multiplikation einen Wert hochskalierten, wurde die Divisionsstruktur verkleinert. Zum Beispiel hat Shannen 6 Stifte und Jen hat 3 mal weniger. Wie viele Stifte hat Jen?

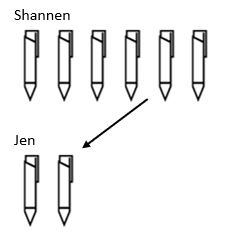
Hier können wir sehen, dass wir, um die Gesamtmenge der Stifte zu finden, die Jen hat, die Menge, die Shannen hatte, nehmen und um einen Skalierungsfaktor von 3 verringern mussten, so dass Jen 2 Stifte hat.

Aus Erfahrung ist dies die schwierigste Teilungsstruktur, die die Schüler verstehen und verstehen müssen, und muss in Verbindung mit der Skalierung sowie der Multiplikation erneut überprüft werden, da dies eine entscheidende Fähigkeit bei der Konvertierung von Messungen und Währungen von einem größeren Betrag in einen kleineren Betrag ist. Z.B. Kilometer in Meilen.

Abteilung Jahr 3

Im Nationalen Lehrplan für Mathematik in England gibt es für jeden umrissenen Bereich der Mathematik sowohl ein gesetzliches als auch ein nicht gesetzliches Element. Das gesetzliche Element ist wie folgt:

Abrufen und Verwenden von Multiplikations- und Divisionsfakten für die Multiplikationstabellen 3, 4 und 8
Schreiben und berechnen Sie mathematische Anweisungen für Multiplikation und Division mit den ihnen bekannten Multiplikationstabellen, einschließlich für zweistellige Zahlen mal einstellige Zahlen, mit mentalen und fortschreitenden zu formalen schriftlichen Methoden
Lösen Sie Probleme, einschließlich Probleme mit fehlenden Zahlen, die Multiplikation und Division beinhalten, einschließlich Probleme mit der Skalierung positiver Ganzzahlen und Korrespondenzprobleme, bei denen n Objekte mit m Objekten verbunden sind.

Nicht-gesetzliche Hinweise und Leitlinien:

Die Schüler entwickeln effiziente mentale Methoden, zum Beispiel durch Kommutativität und Assoziativität (zum Beispiel, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) und Multiplikations- und Divisionsfakten (zum Beispiel unter Verwendung von 3 × 2 = 6, 6 ÷ 3 = 2 und 2 = 6 ÷ 3), um verwandte Fakten abzuleiten (zum Beispiel, 30 × 2 = 60, 60 ÷ 3 = 20 und 20 = 60 ÷ 3).
Die Schüler entwickeln zuverlässige schriftliche Methoden für Multiplikation und Division, beginnend mit Berechnungen von zweistelligen Zahlen durch einstellige Zahlen und weiter zu den formalen schriftlichen Methoden der kurzen Multiplikation und Division.
Die Schüler lösen einfache Probleme in Kontexten und entscheiden, welche der vier Operationen verwendet werden soll und warum. Dazu gehören Mess- und Skalierungskontexte (z. B. viermal so hoch, achtmal so lang usw.) und Korrespondenzprobleme, bei denen m Objekte mit n Objekten verbunden sind (z. B. 3 Hüte und 4 Mäntel, wie viele verschiedene Outfits?; 12 Süßigkeiten zu gleichen Teilen zwischen 4 Kindern geteilt; 4 Kuchen zu gleichen Teilen zwischen 8 Kindern geteilt).

Divisionsaktivitäten Jahr 3

Dies wird keine Lektion an sich abdecken, sondern eine Anleitung geben, wie Division mit einem konzeptionellen Verständnis in dieser Phase gelehrt werden kann. Eine Voraussetzung dafür wäre das Lehren verwandter Multiplikationsfakten, bevor eine verwandte Division unterrichtet wird.

Wenn Sie über Strukturen nachdenken, ist es in diesem Teil der Lernreise der Schüler am besten, bei der Gruppierung und dem Teilen zu bleiben. In den folgenden Beispielen werden wir versuchen, das Verständnis der Schüler für die Division durch 4 zu entwickeln. Es wird dem konkret-bildlich-abstrakten Ansatz folgen.

Es ist oft das Verständnis der Schüler für die Zahl, das ihren Fortschritt in der Division einschränken kann. Besonders wenn es um Gruppierung und Teilen geht, wenn sie nur einen kontinuierlich vom Ganzen wegnehmen.

Lehrer sollten sich von Anfang an auf das stützen, was die Schüler bereits über gerade Zahlen und andere Zahlenfakten wissen, um die Schüler dazu zu bringen, in welcher Zahl auch immer zu zählen.

Zähler können verwendet werden, um verwandte Divisionsfakten zu demonstrieren, da die Schüler beim Aufbau ihres konzeptionellen Verständnisses der Multiplikation Thesen verwendet haben. Fragen wie, ‚Wie viele Gruppen von 4 gibt es?‘ und ‚Wie viele gibt es in jeder Gruppe?‘ sollte gefragt werden, und die Antworten sollten sich darauf beziehen, wie dies Spaltung zeigt.

Lehrer: Wie viele Zähler gibt es?

Kind: Vier

Lehrer: Gut. Dies ist eine Gruppe von vier. Wie viele Vierergruppen gibt es?

Kind: Eins

Lehrer: Ausgezeichnet. Wir haben vier Zähler in einer Gruppe. Wir haben vier Zähler in einer Gruppe zusammengefasst. Was haben wir getan?

Kind: Gruppiert vier Zähler in einer Gruppe.

Lehrer: Brillant. Wenn wir vier Zähler zu einer Gruppe zusammenfassen, haben wir die mathematische Berechnung von vier geteilt durch eins durchgeführt. Welche Berechnung haben wir gemacht?

Kind: Vier geteilt durch eins.

Lehrer: Und wenn wir vier dividiert durch eins lösen, ist die Antwort vier, weil wir eine Gruppe gebildet haben, die vier Elemente enthält. Vier geteilt durch eins ist vier. Was ist vier geteilt durch eins?

Kind: Vier geteilt durch eins ist vier.

Lehrer: Ausgezeichnet

Sie können sehen, wie sich dies für Folgendes wiederholen würde:

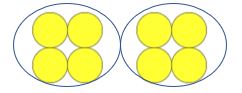
Lehrer: Wie viele Zähler gibt es?

Kind: Acht

Lehrer: Gut, das ist eine Vierergruppe. Wie viele Vierergruppen gibt es?

Kind: Zwei

Lehrer: Ausgezeichnet. Wir haben vier Zähler in einer Gruppe. Wir haben vier Zähler in zwei Gruppen zusammengefasst. Was haben wir getan?

Kind: Gruppiert vier Zähler in zwei Gruppen.

Lehrer: Brillant. Wenn wir vier Zähler in zwei Gruppen gruppieren, haben wir die mathematische Berechnung von acht geteilt durch zwei durchgeführt. Welche Berechnung haben wir gemacht?

Kind: Acht geteilt durch zwei.

Lehrer: Und wenn wir acht geteilt durch zwei lösen, ist die Antwort vier, weil wir zwei Gruppen gebildet haben, die vier Elemente enthalten. Acht geteilt durch zwei ist vier. Was ist acht geteilt durch zwei?

Kind: Acht geteilt durch zwei ist vier.

Lehrer: Ausgezeichnet

Wenn die Schüler anfangen, sich damit vertraut zu machen, können wir zu anderen Modellen wie Cuisenaire-Ruten übergehen.

Hier ist der gesamte Betrag in der oberen Zeile dargestellt und die lila Stange (die in diesem Fall 4 darstellt und wenn Sie andere Blogs in dieser Serie gelesen haben, werden Sie hoffentlich wissen, wie sehr ich mich für ihre Verwendung im Klassenzimmer einsetze und die Schüler werden sich dessen bewusst sein Wert bis dahin) wird verwendet, um zu zeigen, wie viele Gruppen von 4 in den Gesamtbetrag eingehen können.

Die Schüler können dann mit dem Zeichnen von Szenarien fortfahren, die vom Lehrer gelesen werden. Beispielsweise. Es gibt 24 Tasten und sie müssen in 4 gruppiert werden. Wie viele Gruppen gibt es? Die Schüler könnten diese Schaltflächen zeichnen und in 4 usw. gruppieren.

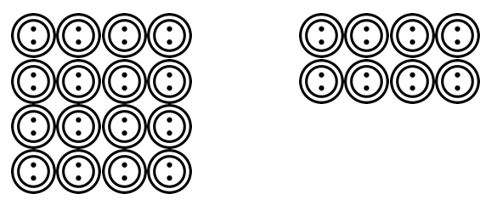
Sobald sich die Schüler daran gewöhnt haben, diese Gruppierungs- oder Teilungsszenarien in einer Reihe von Kontexten visualisieren zu können, können sie mit mathematischen Symbolen zu abstrakteren Darstellungen übergehen.

3 Arbeitsblätter für lange Unterteilungen für die Jahre 3-6

Bereiten Sie Ihre Schüler mit diesen Arbeitsblättern für lange Unterteilungen in ganz KS2 auf lange Unterteilungen vor.

Division Textaufgaben Jahr 3

Textaufgaben im Jahr 3 verwenden üblicherweise die Gruppierungs- oder Freigabestruktur.

Es gibt 40 Kuchen und 10 Studenten. Wie viele Kuchen würde jeder Schüler bekommen?

Da wir wissen, wie viele Gruppen es gibt (10), müssen wir den Betrag pro Gruppe ermitteln. Von den Schülern wird erwartet, dass sie ihr Wissen über die 4-fache Tabelle nutzen, um dies herauszufinden und die Antwort zu erhalten 4.

Abteilung: Argumentation und Problemlösung Jahr 3

Für Argumentation und Problemlösung ist es eine gute Aktivität, ein Wortproblem mit einer Berechnung abzugleichen. Zum Beispiel:

Passen Sie die Wortprobleme an, die gelöst werden, indem Sie 20 geteilt durch 4 kennen.

Es gibt 20 Bleistifte, die in 5er-Packungen verpackt werden. Wie viele in jeder Packung?
Es gab 20 Bleistifte und dann bringt ein Student 4 weitere. Wie viele Bleistifte gibt es jetzt?
Es gibt 20 Bleistifte, die in 4er-Packungen verpackt werden. Wie viele in jeder Packung?
Es gab 20 Bleistifte und dann gehen 4 verloren. Wie viele Bleistifte gibt es jetzt?

Es ist nützlich, die Schüler dazu zu bringen, ihre Erklärungen für jede Frage aufzuschreiben, da sie ihr Denken sehen können. Die Fragen wurden sorgfältig ausgewählt, so dass sich die Zahlen in jeder Frage auf die Zahlen in der Frage beziehen, sodass sich die Schüler auf ihre mathematischen Fähigkeiten verlassen, um die richtige Antwort abzuleiten.

Abteilung Jahr 4

Erinnern Sie sich an Multiplikations- und Divisionsfakten für Multiplikationstabellen bis zu 12 × 12
Verwenden Sie Ortswerte, bekannte und abgeleitete Fakten, um Zahlen zu multiplizieren und zu dividieren, einschließlich: Multiplizieren mit 0 und 1; Dividieren mit 1; Multiplizieren von drei Zahlen

Nicht gesetzliche Hinweise und Anleitungen:

Die Schüler üben weiterhin, Multiplikationstabellen und verwandte Divisionsfakten abzurufen und zu verwenden, um die Sprachgewandtheit zu verbessern.
Die Schüler üben mentale Methoden und erweitern diese auf dreistellige Zahlen, um Fakten abzuleiten (z. B. 600 ÷ 3 = 200 kann aus 2 x 3 = 6 abgeleitet werden).
Die Schüler üben, die formale schriftliche Methode der kurzen Multiplikation und der kurzen Division mit genauen Antworten fließend zu beherrschen
Die Schüler lösen zweistufige Probleme in Kontexten, wählen die geeignete Operation und arbeiten mit immer härteren Zahlen. Dies sollte Korrespondenzfragen wie die Anzahl der Auswahlmöglichkeiten einer Mahlzeit auf einer Speisekarte oder drei Kuchen enthalten, die zu gleichen Teilen von 10 Kindern geteilt werden.

Ideen für Divisionsstunden Jahr 4

In dieser Lektion werde ich mir ansehen, wie Sie beginnen können, kurze Divisionen mit Manipulativen daneben zu unterrichten.

Angenommen, wir werden den Schülern eine kurze Division für die Frage 168 dividiert durch 12 beibringen.

Normalerweise würden wir dies an einer Haltestelle schreiben, die allgemein als Bushaltestelle bezeichnet wird. Interessant ist jedoch, dass verschiedene Orte auf der Welt es anders schreiben.

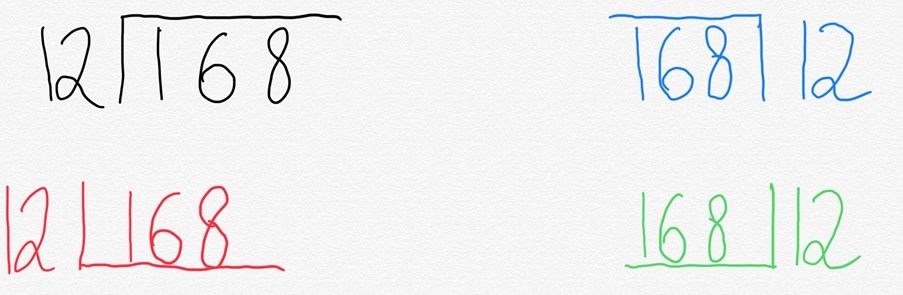
Der Grund dafür ist ganz einfach. Was die ‚Bushaltestelle‘ tatsächlich darstellt, ist eine verkürzte Darstellung eines Rechtecks.

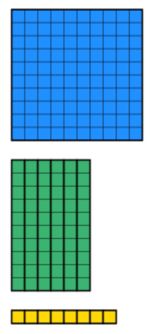
Wenn wir formale kurze Teilung lehren, was wir effektiv sagen, ist, dass Sie sich ein Rechteck vorstellen müssen, wo die Breite 12 ist. Die Gesamtfläche des Rechtecks beträgt 168 und wir versuchen, die fehlende Länge oben zu finden. Wie zeigen wir das mit Manipulativen? Dienes-Blöcke sind hierfür ein nützliches Werkzeug.

Wir wissen, dass der Gesamtbetrag 168 beträgt. Wir müssen also Diene im Wert von 168 mit möglichst geringen Mengen an Blöcken sammeln. Dies wird unten gezeigt.

Wenn wir auf die Frage zurückblicken, wissen wir, dass die Breite 12 beträgt. Das bedeutet, dass wir jetzt die Blöcke so manipulieren müssen, dass wir eine Breite von 12 erhalten. Beachten Sie, dass das Rechteck solide sein muss und keine fehlenden Teile haben darf. Zum Beispiel wäre das Folgende nicht erlaubt, obwohl 12 Einheiten die Breite hinuntergehen.

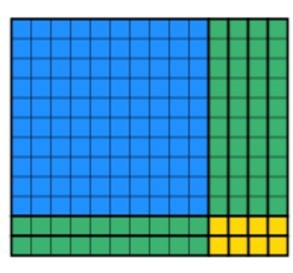
Stattdessen können die Schüler zwei 10er-Blöcke drehen, um Folgendes zu erhalten. Beachten Sie, dass sich in jeder Spalte 12 befindet und es sich um ein festes Objekt handelt.

Der letzte Teil, den die Schüler tun müssen, ist, die verbleibenden Blöcke zu verwenden, um ein quadratisches Rechteck zu erstellen, während die Breite 12 beibehalten wird. Dies kann einige Zeit dauern, aber mit etwas Übung werden die Schüler schneller. Nach einiger Zeit werden die Schüler dies produzieren:

Wir können sehen, dass alle Blöcke im Wert von 168 aufgebraucht sind und dass die Breite immer noch 12 beträgt. Um die Antwort zu finden, müssen die Schüler die Länge zählen, in diesem Fall 14. Ich habe beide Methoden unten überlagert, damit Sie unten sehen können, wie sie sich ergänzen.

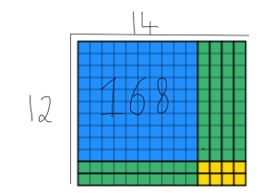
Dies ist eine nützliche Strategie, um Schüler im Jahr zu unterrichten 4 da es massive Auswirkungen auf andere Bereiche des Lehrplans gibt, die den Schülern bereits zugänglich sind.

Obwohl sie es vielleicht noch nicht erkennen, wurden sie durch das Unterrichten einer kurzen Teilung wie dieser bereits in Perimeter und Area eingeführt – überlegen Sie, wie viel Unterrichtszeit gespart werden kann, wenn diese Verbindung hergestellt wird. Darüber hinaus überträgt sich dieser Ansatz auf das algebraische Denken.

Division Word Problems Jahr 4

Von den Schülern wird erwartet, dass sie sich auf ihr Wissen über den Stellenwert stützen, um divisionsbasierte Probleme zu lösen.

In einem Obstgarten wurden in einer Saison 4.800 Äpfel angebaut. Sie werden in 4er-Packungen verpackt, bevor sie auf den Markt kommen. Wie viele Packungen gibt es?

Hier sollten die Schüler die Tatsache nutzen, dass 4 x 12 = 48 ist und da 4.800 hundertmal mehr als 48 ist, muss 12 auch mit 100 multipliziert werden, um 1.200 zu erhalten

Division: Argumentation und Problemlösung Jahr 4

Ist es immer, manchmal oder nie wahr, dass die Summe von drei geraden Zahlen durch 4 teilbar ist?

Diese Frage gibt den Schülern reichlich Gelegenheit, innerhalb der Parameter der Frage zu experimentieren. Schüler, die mehr Unterstützung benötigen, können sich einstellige gerade Zahlen ansehen, und die Schüler können zu dem aufsteigen, womit sie sich wohl fühlen.

Bei offenen Fragen wie dieser ist es gut, eine Mindestanforderung für die Anzahl der Versuche anzugeben, die die Schüler machen sollten, da sie sich sonst oft für das absolute Minimum entscheiden.

Die Antwort auf diese Frage ist manchmal.

Ein schneller Trick, um zu wissen, ob eine Zahl teilbar ist, besteht darin, die letzten 2 Ziffern der Zahl zu betrachten und festzustellen, ob diese durch 4 teilbar sind. Wenn zum Beispiel ein Kind die Summe von 34, 36 und 38 gefunden und 108 erhalten hat, weiß ich als Lehrer, dass diese Zahl durch 4 teilbar ist, da die letzten beiden Ziffern (08) 8 ergeben und durch 4 teilbar sind. Wenn ein Kind 34, 36 und 48 wählt, um 118 zu erhalten, weiß ich, dass dies nicht durch 4 teilbar ist, da 18 – die letzten beiden Ziffern von 118 – nicht durch 4 teilbar sind.

Abteilung Jahr 5

Multiplizieren und dividieren Sie Zahlen mental anhand bekannter Fakten
Teilen Sie Zahlen bis zu 4 Ziffern durch eine einstellige Zahl unter Verwendung der formalen schriftlichen Methode der kurzen Division und interpretieren Sie die Reste entsprechend dem Kontext
Multiplizieren und dividieren Sie ganze Zahlen und solche mit Dezimalstellen mit 10, 100 und 1000
Lösen Sie Probleme mit Multiplikation und Division, einschließlich multiples, Quadrate und Würfel
Lösen Sie Probleme mit Addition, Subtraktion, Multiplikation und Division und eine Kombination aus diese, einschließlich des Verständnisses der Bedeutung des Gleichheitszeichens
Lösen Probleme mit Multiplikation und Division, einschließlich Skalierung durch einfache Brüche und Probleme mit einfachen Raten.

Nicht-gesetzliche Hinweise und Leitlinien:

Die Schüler interpretieren nicht ganzzahlige Antworten auf die Division, indem sie die Ergebnisse je nach Kontext unterschiedlich ausdrücken, einschließlich mit Resten, als Brüche, als Dezimalstellen oder durch Runden (z. B. 98 ÷ 4 = = 24 r 2 = 24 = 24,5 ≈ 25).
Schüler verwenden Multiplikation und Division als Inverse, um die Einführung des Verhältnisses in der 6. Klasse zu unterstützen, z. B. durch Multiplikation und Division mit Potenzen von 10 in Maßstabszeichnungen oder durch Multiplikation und Division mit Potenzen von 1.000 bei der Umrechnung zwischen Einheiten wie Kilometern und Metern.

Division im Jahr 5

Division im Jahr 5 schreitet durch die Verwendung von Resten in Antworten fort. Für diese Lektion werde ich mir andere use Manipulatives ansehen, mit denen Lehrer die 4-mal-1-stellige Division unterrichten können.

Wenn die Frage 5.642 geteilt durch 4 wäre, könnten wir dies mithilfe eines Ortswertdiagramms und Ortswertzähler darstellen, wie wir unten sehen können.

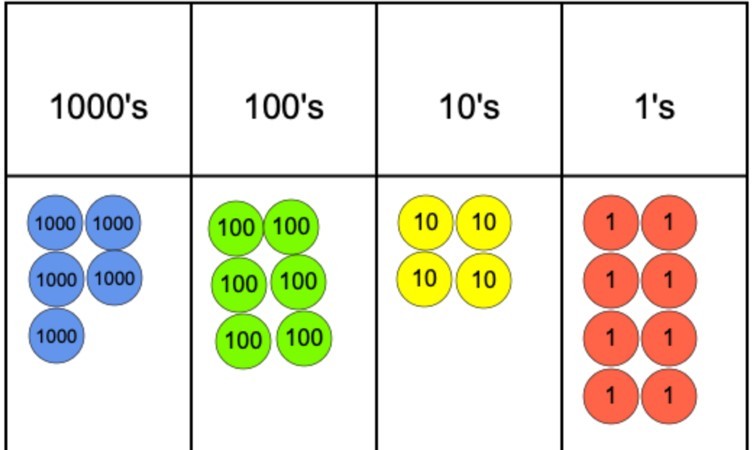
Der nächste Schritt wäre, die Zähler in 4 zu gruppieren, da dies unser Divisor ist. Wie zu sehen ist, kommen wir jedoch schnell zu einem Problem in der Spalte 1000, da wir 4 der Zähler gruppieren können, aber dann den verbleibenden Zähler nicht in einer Gruppe von 4 gruppieren können.

Um dieses Problem zu beheben, kann der nicht gruppierte 1000-Zähler gegen zehn 100-Zähler eingetauscht werden. Diese können dann in Gruppen von 4 gruppiert werden und dies kann passieren, ohne dass 100s-Zähler übrig bleiben. Von dort aus ist es ein einfacher Fall, dann zu den 10ern und schließlich zu denen zu wechseln.

Da es neun 1s-Zähler gibt, können wir 8 davon in 2 Gruppen und 4 gruppieren und behaupten, dass noch einer übrig ist *. Um die Antwort zu finden, müssen Sie lediglich die Anzahl der in jedem Stellenwert erstellten Gruppen zählen und diese verwenden, um die Ziffern zu schreiben, um die endgültige Antwort zu erstellen. In diesem Fall wäre die Antwort 1.412 Rest 1.

*Wenn Sie Dezimalzahlen betrachten, können Sie den verbleibenden 1s-Zähler gegen zehn 0,1-Zähler eintauschen und die Division wie oben beschrieben fortsetzen. Schüler, die mit diesem Modell vertraut sind, sind nützlich, da es helfen kann, die Division mit Dezimalstellen zu entmystifizieren, mit denen Schüler zu kämpfen haben können. Dies hilft ihnen zu erkennen, dass es sich um eine Fortsetzung eines Prozesses handelt, mit dem sie bereits vertraut sind, und nicht um etwas Neues.

Teilungsprobleme Jahr 5

Beim Teilen in Jahr 5 stoßen die Schüler auf Szenarien, in denen sie ihre Antwort aufrunden müssen, damit die Antwort im Kontext Sinn ergibt. Eine geeignete Frage, die dies demonstriert, wäre ungefähr die folgende:

Eine Schule plant eine sozial distanzierte Disco, in der sie jedem Schüler 250 ml Saft anbieten möchten. Sie können 2-Liter-Flaschen Saft kaufen. Sie erwarten, dass 33 Studenten ankommen, also wissen Sie, dass sie 8,25 Liter Saft ausgeben werden. Wie viele Flaschen Saft müssen sie kaufen?

Eine häufige Antwort ist, dass die Schüler 4 und ein Viertel sagen. Da Sie jedoch keine Viertelflasche kaufen können, lautet die richtige Antwort in diesem Fall 5 Flaschen Saft, um sicherzustellen, dass alle Schüler teilnehmen können.

Abteilung: Argumentation und Problemlösung Jahr 5

Wie oben erwähnt, werden die Schüler im Jahr 5 auf Szenarien innerhalb der Abteilung stoßen, in denen sie entscheiden müssen, ob eine Antwort aufgerundet oder abgerundet werden soll. Zum Beispiel, wenn eine Frage die Schüler bittet, herauszufinden, wie viele Busse für eine Schulfahrt benötigt werden.

Schüler dazu zu bringen, ihre eigenen Probleme mit einer Reihe von bereitgestellten Kontexten zu erstellen, kann eine wirklich herausfordernde Aktivität sein, die die Schüler dazu bringt, mathematisch über Kontext und Division nachzudenken.

Die Schüler können dann diese Fragen, die sie erstellt haben, mit einem Partner austauschen und sie dann lösen und mit dem ursprünglichen Fragenersteller überprüfen, ob sie die richtige Antwort haben.

Abteilung Jahr 6

dividieren Sie Zahlen bis zu 4 Ziffern durch eine zweistellige ganze Zahl unter Verwendung der formalen schriftlichen Methode der langen Division und interpretieren Sie Reste als ganze Zahlenreste, Brüche oder durch Runden, je nach Kontext
Dividieren Sie Zahlen bis zu 4 Ziffern durch eine zweistellige Zahl unter Verwendung der formalen schriftlichen Methode der kurzen Division gegebenenfalls Interpretieren von Resten gemäß dem Kontext
Führen Sie mentale Berechnungen durch, auch mit gemischten Operationen und großen zahlen
Identifizieren Sie gemeinsame Faktoren, gemeinsame Vielfache und Primzahlen
Nutzen Sie ihr Wissen über die Reihenfolge der Operationen, um Berechnungen mit den vier Operationen durchzuführen

Nicht gesetzliche Hinweise und Anleitungen:

Lösen Sie Probleme mit Addition, Subtraktion, Multiplikation und Division
Verwenden Sie die Schätzung, um die Antworten auf Berechnungen zu überprüfen und im Kontext eines Problems einen angemessenen Genauigkeitsgrad zu bestimmen.

Division Lesson Ideas Year 6

Sophie Bartlett (@_MissieBee) hat hier einen ausgezeichneten Blog erstellt (Link zu Sophies Blog über das Unterrichten von Long Division), in dem beschrieben wird, wie sie Long Division für ein Jahr unterrichten würde 6 Klasse. Da Long Division das einzige neue Lernen zur Division für das 6. Jahr ist, ist dies ein idealer Weg, um das Verfahren der Long Division einzuführen.

Divisionsfragen Jahr 6

Ein typisches Divisionswortproblem, auf das ein Schüler des 6. Jahres stoßen würde, wäre:

Eine Schule sammelte £ 3.146 aus einem Kuchenverkauf. 104 Eltern nahmen an der Veranstaltung teil. Wenn alle Eltern gleich viel Geld ausgegeben haben, wie viel hat jeder Elternteil ausgegeben?

Hier würde von den Schülern erwartet, dass sie die Long Division-Methode verwenden, um diese Frage zu lösen und die Antwort £ 30.25 zu erhalten.

Abteilung: Argumentation und Problemlösung Jahr 6

Mit etwas Prozeduralem wie der langen Division besteht eine gute Argumentationsaktivität darin, die Schüler dazu zu bringen, Fehler zu finden. Diese Ressourcen bieten eine große Bank solcher Aktivitäten. Wie wir aus der Frage unten sehen können, haben die Schüler die ganze harte Arbeit geleistet, aber ein unvorsichtiger Fehler beim Zählen der Gruppen von 59 bedeutet, dass das Kind glaubte, 59 x 7 sei 472 und nicht 59 x 8.

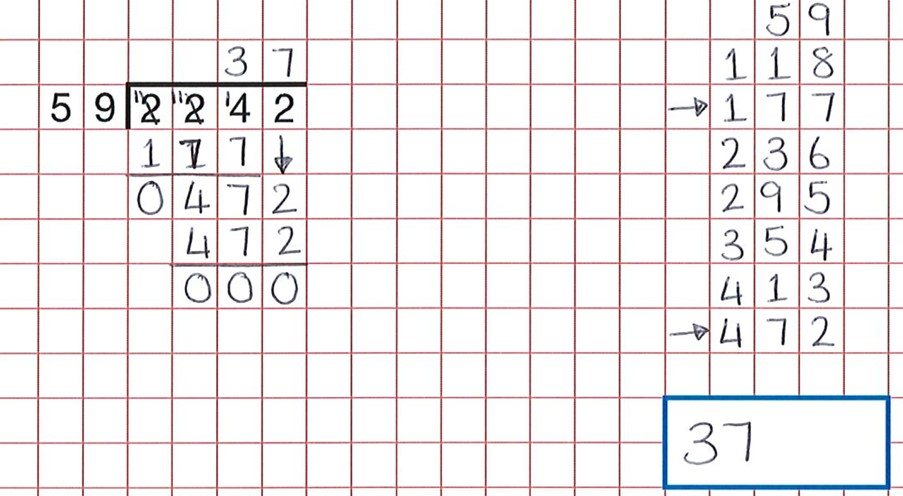
Die richtige Antwort wäre 38 gewesen.

Division ist ein wichtiges Mathematikthema, nicht nur bei KS2, sondern in Mathematik als Ganzes. Hoffentlich hat Ihnen dieser Beitrag einige gute Ideen gegeben, damit Ihre Schüler zuversichtlich damit umgehen können.

Online-1-zu-1-Mathematikunterricht, dem Schulen und Lehrer vertrauen
Jede Woche unterstützen die Mathe-Tutoren von Third Space Learning Tausende von Grundschulkindern mit wöchentlichen Online-1-zu-1-Lektionen und Mathe-Interventionen. Seit 2013 haben wir über 100.000 Kindern geholfen, selbstbewusstere und fähigere Mathematiker zu werden. Erfahren Sie mehr oder fordern Sie ein individuelles Angebot an, um mit uns über Ihre Bedürfnisse zu sprechen und wie wir Ihnen helfen können.

Grundschulunterricht, der auf die Bedürfnisse jedes Kindes zugeschnitten ist und dem nationalen Lehrplan genau folgt.

Teaching Division KS2: Ein Leitfaden für Grundschullehrer von Jahr 3 bis Jahr 6