In diesem Handbuch erkläre ich anhand eines Beispiels, was die Standardfehlerformel ist und wie sie verwendet wird, um den Standardfehler zu ermitteln.
Was ist der Standardfehler?
Der Standardfehler (SE), manchmal auch als Standardfehler des Mittelwerts (SEM) bezeichnet, ist eine Statistik, die der Standardabweichung einer Stichprobenverteilung relativ zum Mittelwert entspricht. Aber was ist das eigentlich?
Angenommen, Sie interessieren sich für das Durchschnittsalter, in dem Menschen in Großbritannien mit Alzheimer diagnostiziert werden. Es ist nicht möglich, dies für jeden in Großbritannien zu bestimmen, Daher nehmen die Forscher eine Stichprobenpopulation, um eine Gesamtgröße zu verallgemeinern. Zum Beispiel können 10.000 britische Menschen mit der Krankheit analysiert werden und werden verwendet, um das Durchschnittsalter der Diagnose zu generieren. Wenn Sie dies an einer Stichprobe von 5.000 Patienten tun, erhalten Sie möglicherweise ein Durchschnittsalter der Diagnose von 61,5 Jahren. Wenn Sie jedoch die Probenanalyse an einer separaten Zufallsstichprobe von 10.000 anderen Patienten durchführen, erhalten Sie möglicherweise ein Durchschnittsalter von 62,3 Jahren. Nehmen wir an, hypothetisch natürlich, wenn Sie in der Lage wären, alle Menschen in Großbritannien zu analysieren, die an Alzheimer leiden, um die tatsächliche Zahl zu erhalten, könnten Sie am Ende 64,3 Jahre alt werden. Sie können feststellen, dass die Zahlen aus den Stichprobenpopulationen (61,5 und 62,3 Jahre) von der tatsächlichen Zahl (64,3 Jahre) abweichen. Diese Variation der Mittelwerte wird erwartet, und wenn Sie die Anzahl der Personen in Ihrer Stichprobenpopulation erhöhen, erhalten Sie einen Wert, der näher an der tatsächlichen Zahl liegt. Genau das stellt der Standardfehler dar. Der Standardfehler bezeichnet diese Variation der Mittelwerte zwischen den Stichprobenpopulationen.
Zur weiteren Lektüre empfehle ich Ihnen, die kurze Statistiknotiz der Professoren Douglas Altman und Martin Bland zu lesen, die im British Medical Journal veröffentlicht wurde. Es ist ein hilfreicher Einblick in den Standardfehler und den Unterschied zur Standardabweichung.
Die Standardfehlerformel
Um den Standardfehler zu berechnen, benötigen Sie zwei Informationen: die Standardabweichung und die Anzahl der Stichproben im Datensatz. Der Standardfehler wird berechnet, indem die Standardabweichung durch die Quadratwurzel der Anzahl der Stichproben dividiert wird.
Hier ist die vollständige kommentierte Standardfehlerformel:
Beispiel
Um die Standardfehlerformel besser zu verstehen, kann es hilfreich sein, ein Beispiel durchzugehen. Angenommen, wir haben 80 Einwohner und interessieren uns für ihre Größe. Wir messen ihre Höhe und berechnen die Standardabweichung als 30,6 cm. Wir müssen nun diese Werte in unsere Gleichung einfügen:
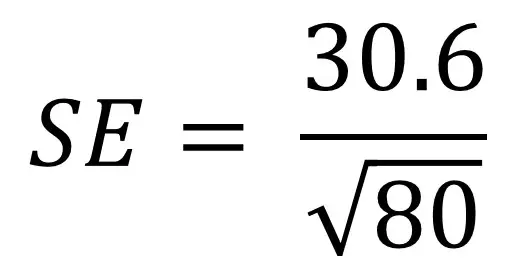Wenn Sie sich mit der Eingabe von Gleichungen in Taschenrechner nicht wohl fühlen, können Sie die Formel in überschaubare Teile aufteilen. Hier sind die Schritte, die Sie unternehmen können.
- Berechnen Sie zunächst die Quadratwurzel aus der Anzahl der Stichproben (n). In diesem Fall ist n 80. Die Quadratwurzel von 80 ist 8,94.
- Als nächstes teilen Sie die Standardabweichung (30,6) durch die Quadratwurzel von 80 (8,94). Dies ergibt einen Wert von 3,42.
- Daher beträgt der Standardfehler in unserer Bevölkerung für die Höhe 3,42 cm.