Eckpunkte, Flächen und Kanten kommen in der Geometrie der Grundschule häufig vor, wenn Kinder die Eigenschaften von 3D-Formen kennenlernen. Hier erklären wir, was diese jeweils bedeuten und wie die Anzahl der Scheitelpunkte, Flächen und Kanten für jede Form ermittelt wird. Wir geben auch die Anzahl der Kanten, Flächen und Scheitelpunkte der häufigsten Formen an.
Dieses Vokabular wird in der 2. Klasse in den nationalen Lehrplan aufgenommen, sodass die folgenden Informationen mit Schülern während der gesamten Grundschulzeit verwendet werden können. Sogar Schüler der 1. Klasse können sich auf diese Weise mit den Eigenschaften von Formen auseinandersetzen, wenn Sie ihnen einen Vorsprung verschaffen möchten!
Was sind Eckpunkte in Formen?
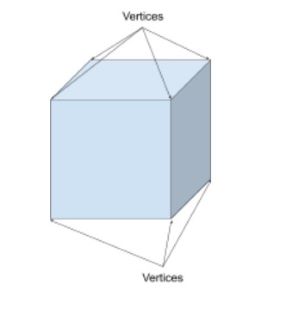
Eckpunkte in Formen sind die Punkte, an denen sich zwei oder mehr Liniensegmente oder Kanten treffen (wie eine Ecke). Der Singular der Eckpunkte ist Vertex. Zum Beispiel hat ein Würfel 8 Eckpunkte und ein Kegel einen Eckpunkt.
Eckpunkte werden manchmal Ecken genannt, aber wenn es um 2D- und 3D-Formen geht, wird das Wort Eckpunkte bevorzugt.
Ein Würfel hat 8 Eckpunkte. 7 sind hier sichtbar und einer ist versteckt.
Was sind Kanten?
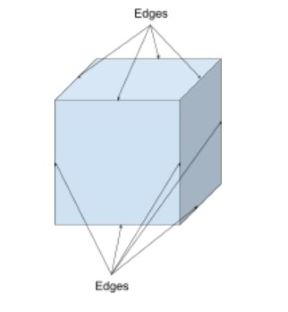
Kanten sind die Liniensegmente, die einen Scheitelpunkt mit einem anderen verbinden und an denen sich auch die Flächen der Form treffen. Diese können verwendet werden, um 2D- und 3D-Formen zu beschreiben.
Obwohl viele Formen gerade Linien und gerade Kanten haben, gibt es Formen mit gekrümmten Kanten, z. B. eine Halbkugel. Ein Würfel hat 12 gerade Kanten, wie unten zu sehen; 9 sind sichtbar und 3 sind ausgeblendet.

FREE 3D Shapes Independent Recap Worksheets
Helfen Sie Ihren Schülern der 2. Klasse (und älter), Scheitelpunkte, Flächen und Kanten mit unseren kostenlosen Independent Recap Worksheets zu überarbeiten.
Was sind Gesichter?
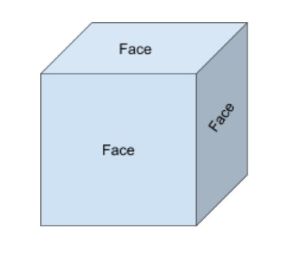
Flächen sind die flache Oberfläche einer festen Form. Zum Beispiel hat ein Quader 6 Gesichter. Wenn Sie über 2D- und 3D-Formen nachdenken, ist es wichtig zu wissen, dass eine 2D-Form lediglich das Gesicht einer 3D-Form darstellt.
Es ist auch wichtig zu wissen, dass es unmöglich ist, 2D-Formen physisch zu handhaben, da unsere Realität in 3-Dimensionen konstruiert ist, da wir von 3-dimensionalen Formen umgeben sind. Wenn sich in Ihrem Klassenzimmer eine Schublade mit der Bezeichnung ‚2D-Formen‘ befindet, sollte diese daher entfernt werden, da sie Kindern ein Missverständnis beibringt. Obwohl es sich um ein interaktives Konzept für den Unterricht handelt, können 2D-Formen nur als 2-dimensionale Zeichnungen existieren.
Sie können sowohl flache als auch gekrümmte Flächen haben, aber ich finde es hilfreich, gekrümmte Flächen als gekrümmte Flächen zu bezeichnen, da dies gut zum Erscheinungsbild der Form passt.
Auf dem Würfel darunter sind drei Gesichter sichtbar und drei verborgen.
Eckpunkte, Flächen und Kanten gängiger 3D-Formen
Wie viele Flächen, Kanten und Eckpunkte hat ein Quader?
Ein Quader hat 8 Eckpunkte.
Ein Quader hat 12 Kanten.
Ein Quader hat 6 Flächen.

Wie viele Flächen, Kanten und Eckpunkte hat ein Zylinder?
Ein Zylinder hat 0 Eckpunkte.
Ein Zylinder hat 2 Kanten.
Ein Zylinder hat 2 Flächen und 1 gekrümmte Oberfläche.

Wie viele Flächen, Kanten und Eckpunkte hat eine Halbkugel?
Eine Halbkugel hat 0 Eckpunkte.
Eine Halbkugel hat 1 gekrümmte Kante.
Eine Halbkugel hat 1 Fläche und 1 gekrümmte Oberfläche.

Wie viele Flächen, Kanten und Eckpunkte hat ein Kegel?
Ein Kegel hat 1 Scheitelpunkt.
Ein Kegel hat 1 Kante.
Eine Halbkugel hat 1 Fläche und 1 gekrümmte Oberfläche.

Wie viele Flächen, Kanten und Eckpunkte hat ein Tetraeder?
Ein Tetraeder hat 4 Eckpunkte.
Ein Tetraeder hat 6 Kanten.
Ein Tetraeder hat 4 Flächen.

Wie viele Flächen, Kanten und Eckpunkte hat eine Kugel?
Eine Kugel hat 0 Eckpunkte.
Ein Tetraeder hat 0 Kanten.
Ein Tetraeder hat 1 gekrümmte Oberfläche.

Wie viele Flächen, Kanten und Eckpunkte hat ein Prisma?
Ein Prisma ist ein festes Objekt, eine geometrische Form oder ein Polyeder, bei dem die Flächen beider Enden die gleiche Form haben. Daher werden die Schüler während ihrer Schulzeit auf viele Arten von Prismen stoßen. Übliche sind Würfel, Quader, dreieckige Prismen, fünfeckige Prismen und sechseckige Prismen.
| Form | Bildlich | Gesichter | Kanten | Eckpunkte |
|---|---|---|---|---|
| Dreiecksprisma | 5 | 9 | 6 | |
| Fünfeckiges Prisma | 7 | 15 | 10 | |
| Hexagonales Prisma | 8 | 18 | 12 | |
| Cube | 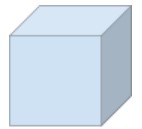 |
6 | 8 | 12 |
| Quader |  |
6 | 8 | 12 |
Wann lernen Kinder in der Grundschule Scheitelpunkte, Flächen und Kanten?
Kinder müssen im Jahr 2 beim Geometriestudium förmlich in das Vokabular der Eckpunkte, Flächen und Kanten eingeführt werden. Lehrer können jedoch die Wahl treffen, dieses Vokabular früher einzuführen.
Jahr 2 Schüler sollten in der Lage sein:
- Identifizierung und Beschreibung der Eigenschaften von 3D-Formen, einschließlich der Anzahl der Kanten, Scheitelpunkte und Flächen
Die nicht gesetzlich vorgeschriebene Anleitung besagt, dass:
- Die Schüler behandeln und benennen eine Vielzahl gängiger 2D- und 3D-Formen, darunter: Vierecke und Polygone sowie Quader, Prismen und Kegel, und identifizieren die Eigenschaften jeder Form (z. B. Anzahl der Seiten, Anzahl der Flächen). Die Schüler identifizieren, vergleichen und sortieren Formen anhand ihrer Eigenschaften und verwenden Vokabeln wie Seiten, Kanten, Ecken und Flächen präzise.
Ab diesem Zeitpunkt bezieht sich der nationale Lehrplan nicht mehr explizit auf Scheitelpunkte, Flächen und Kanten, sodass Lehrer in anderen Jahrgangsgruppen dieses Vokabular weiterhin verwenden müssen, wenn sie shape
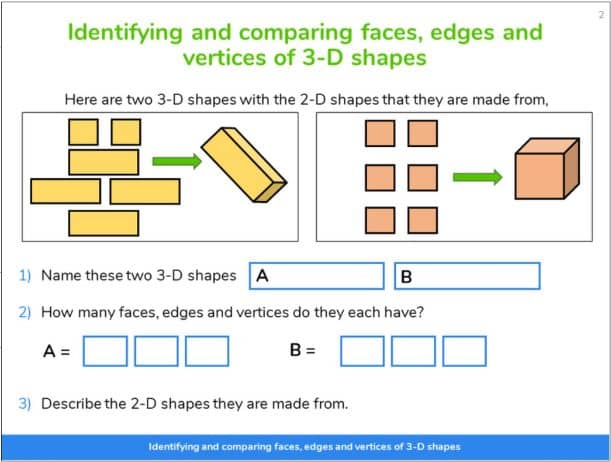
Wie beziehen sich Eckpunkte, Flächen und Kanten auf andere Bereiche der Mathematik?
Die Schüler nutzen das Wissen über Scheitelpunkte, Flächen und Kanten, wenn sie 2D-Formen sowie 3D-Formen betrachten. Zu wissen, was Kanten sind, und sie auf zusammengesetzten Formen zu identifizieren, ist entscheidend, um den Umfang und die Fläche von 2D-zusammengesetzten Formen zu finden. Es ist eine wichtige Grundlage für spätere Jahre im Umgang mit verschiedenen mathematischen Theoremen, wie Graphentheorie und Parabeln.
Wie beziehen sich Ecken, Flächen und Kanten auf das wirkliche Leben?
Jedes Objekt im wirklichen Leben hat Ecken, Flächen und Kanten. Zum Beispiel ist ein Kristall ein Oktaeder – er hat acht Flächen, zwölf Kanten und sechs Eckpunkte. Die Kenntnis dieser Eigenschaften für verschiedene dreidimensionale Formen legt den Grundstein für verschiedene Branchen wie Architektur, Innenarchitektur, Maschinenbau und mehr.
Eckpunkte, Flächen und Kanten Beispielfragen
1. Erklären Sie, was ein Scheitelpunkt ist.
(Antwort: Ein Scheitelpunkt ist, wo sich zwei Linien treffen)
2. Wie viele Kanten hat ein Dreiecksprisma?
(Antwort: 9)
3. Wie viele Eckpunkte hat ein Kegel?
(Antwort: 1 Scheitelpunkt)
4. Wie viele Gesichter hat ein Quader? Was sind die 2D-Formen dieser Gesichter?
(Antwort: 6 Gesichter. Sie können 2 quadratische Flächen und 4 rechteckige Flächen oder nur 6 rechteckige Flächen haben.)
5. Für alle gängigen Prismen (Würfel, Quader, Dreiecksprismen, Fünfeckprismen und sechseckige Prismen) addieren Sie die Flächen und Eckpunkte und subtrahieren Sie die Kanten. Was fällt Ihnen an den Antworten auf?
(Antwort: Die Antwort ist immer 2. Dies ist bekannt als Eulers Formel (Anzahl der Eckpunkte – Anzahl der Kanten + Anzahl der Flächen = 2)
Sie fragen sich, wie Sie Ihren Kindern andere wichtige mathematische Vokabeln erklären können? Schauen Sie sich unser primäres Mathematikwörterbuch an oder probieren Sie diese aus:
- Was ist Mathe Mastery?
- Was sind 2D-Formen?
- Was sind 3D-Formen?
Auf dem Third Space Learning Maths Hub finden Sie zahlreiche Geometrieunterrichtspläne und druckbare Arbeitsblätter für Grundschüler.
Online-1-zu-1-Mathematikunterricht, dem Schulen und Lehrer vertrauen
Jede Woche unterstützen die Mathe-Tutoren von Third Space Learning Tausende von Grundschulkindern mit wöchentlichen Online-1-zu-1-Lektionen und Mathe-Interventionen. Seit 2013 haben wir über 100.000 Kindern geholfen, selbstbewusstere und fähigere Mathematiker zu werden. Erfahren Sie mehr oder fordern Sie ein individuelles Angebot an, um mit uns über Ihre Bedürfnisse zu sprechen und wie wir Ihnen helfen können.
Unser Online-Mathematikunterrichtsprogramm bietet jedem Kind seinen eigenen professionellen Eins-zu-Eins-Mathematiklehrer