En esta guía explicaré qué es la fórmula de error estándar y cómo usarla para resolver el error estándar mediante el uso de un ejemplo.
¿Cuál es el error estándar?
El error estándar (SE), a veces denominado error estándar de la media (SEM), es una estadística que corresponde a la desviación estándar de una distribución de muestreo, en relación con el valor medio. Pero, ¿qué es eso en realidad?
Diga que está interesado en la edad promedio a la que se diagnostica la enfermedad de Alzheimer a las personas en el Reino Unido. No es factible determinar esto para todos en el Reino Unido, por lo tanto, los investigadores toman una muestra de población para generalizar una cifra general. Por ejemplo, se pueden analizar 10.000 británicos con la enfermedad y se utilizarán para generar la edad media de diagnóstico. Si hace esto en una muestra aleatoria de 5,000 pacientes, puede obtener una edad promedio de diagnóstico de 61.5 años. Sin embargo, si realiza el análisis de muestras en una muestra aleatoria separada de otros 10,000 pacientes, puede obtener una edad promedio de 62.3 años. Digamos, hipotéticamente hablando, por supuesto, que si pudieras analizar a todas las personas en el Reino Unido que tienen la enfermedad de Alzheimer para obtener la cifra real, podrías terminar con 64,3 años. Se puede observar que las cifras obtenidas de las poblaciones de la muestra (61,5 y 62,3 años) difieren de la cifra real (64,3 años). Se espera esta variación en los valores medios, y a medida que aumente el número de personas en su población de muestra, obtendrá un valor que se aproxima a la cifra real. Esto es exactamente lo que representa el error estándar. El error estándar significa esta variación en los valores medios entre las poblaciones de la muestra.
Para más información, le sugiero que lea la breve Nota Estadística de los profesores Douglas Altman y Martin Bland publicada en el British Medical Journal. Es una visión útil de lo que es el error estándar y cuál es la diferencia con la desviación estándar.
La fórmula de error estándar
Para calcular el error estándar, debe tener dos piezas de información: la desviación estándar y el número de muestras en el conjunto de datos. El error estándar se calcula dividiendo la desviación estándar por la raíz cuadrada del número de muestras.
Aquí está la fórmula de error estándar anotada completa:
Ejemplo
Para comprender mejor la fórmula de error estándar, puede ser útil revisar un ejemplo. Digamos que tenemos una población de 80 personas y estamos interesados en su altura. Medimos su altura y calculamos la desviación estándar como 30,6 cm. Ahora necesitamos conectar estos valores en nuestra ecuación:
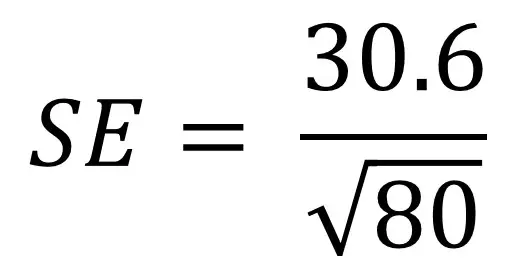Si no se siente cómodo introduciendo ecuaciones en calculadoras, puede dividir la fórmula en trozos manejables. Estos son los pasos que puede seguir.
- En primer lugar, calcular la raíz cuadrada del número de muestras (n). En este caso, n es 80. La raíz cuadrada de 80 es 8.94.
- A continuación, divida la desviación estándar (30.6) por la raíz cuadrada de 80 (8.94). Hacer esto da un valor de 3.42.
- Por lo tanto, el error estándar en nuestra población para la altura es de 3,42 cm.