La División en Key Stage 2 forma la última parte de las «Cuatro Operaciones», los cuatro conceptos matemáticos básicos que los alumnos deben conocer. Este blog le ayudará a asegurarse de que todos sus alumnos, desde Year 3 hasta Year 6, puedan abordar la división con la confianza que necesitan para tener éxito.
La División en matemáticas de KS2 se basa en lo que se ha aprendido en KS1. Al final de Y2, los estudiantes en el estándar esperado podrán » recordar y usar datos de multiplicación y división para las tablas de multiplicación 2, 5 y 10, incluido el reconocimiento de números pares e impares.»
Para los profesores de Year 3, siempre es una buena idea asegurarse de que los estudiantes los conozcan muy bien. Con esto, no quiero decir simplemente que pueden repetir los hechos de la división, sino que realmente entienden cómo representar estos hechos con representaciones concretas, explicaciones verbales y a través de otros métodos pictóricos.
Los estudiantes que no son capaces de hacer esto, sin embargo, son capaces de decirle verbalmente los hechos de la división, tienen una comprensión muy superficial de la división y para que puedan progresar en actividades de resolución de problemas más difíciles, profundizar su comprensión conceptual de la división es una necesidad en el Año 3.
El Currículo Nacional coloca la división dentro de la misma sección que la multiplicación para los Años 3-5 y la coloca dentro de una sección llamada «Cuatro Operaciones» en el Año 6. Las partes del Plan de estudios Nacional se refieren únicamente a las que mencionan específicamente la división. Los demás elementos de esas secciones se pueden encontrar en el blog sobre multiplicación o suma y resta cuando corresponda.
¿Qué Es La División?
La división es una de las Cuatro Operaciones, los cuatro conceptos matemáticos básicos que los alumnos deben conocer, junto con la suma, la resta y la multiplicación.
Cuando la multiplicación combina un número varias veces, la división es lo contrario: calcular cuántas veces un número está contenido dentro de otro. Por ejemplo, dividir 10 entre 2 es preguntar cuántas veces 2 está contenido dentro de 10.

de las intervenciones matemáticas en línea de Third Space Learning.
División de enseñanza KS2-La Teoría
La división es la inversa de la multiplicación. Al igual que con el blog de multiplicación, la enseñanza de la división contiene tres estructuras subyacentes que, cuando se combinan con hechos de división y comprensión conceptual, darán a los estudiantes la mejor oportunidad de tener éxito al resolver problemas relacionados con la división.
Las tres estructuras comparten, agrupan y escalan. Si bien no hay tiempo suficiente para explorarlos en profundidad, lo que sigue será solo una breve introducción a ellos.
Compartir y agrupar son el inverso de la multiplicación como suma repetida. Compartir es un concepto estructural que se introduce en KS1 y anteriores donde, como su nombre indica, una cantidad se comparte en grupos iguales.
Por ejemplo, se comparten 12 manzanas entre 3 estudiantes. ¿Cuántas manzanas recibe cada estudiante? Aquí conocemos la cantidad total (12 manzanas) y, lo que es más importante, sabemos en qué cantidad vamos a compartir (3). Dependiendo de dónde se encuentren los estudiantes en su viaje matemático, pueden restar repetidamente por algún número (1, 2, 3 o 4) de la cantidad en tres pilas que representan a los tres estudiantes.
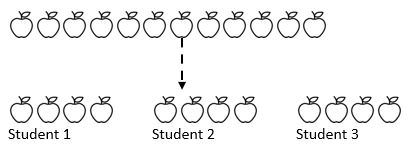
Como podemos ver en lo anterior, la cantidad total se ha compartido en tres grupos iguales.
Agrupar es similar a compartir, pero lo que sabemos es ligeramente diferente en comparación con compartir. En la estructura de compartir, sabemos la cantidad de grupos en los que se llevará a cabo el intercambio. En la estructura de agrupación, sabemos la cantidad en cada grupo, pero no el número de grupos reales que hay.
Por ejemplo, 12 manzanas se comparten en grupos de 4. Cuántos grupos hay? Si bien esta pregunta es muy similar a la anterior, ahora toma la estructura de agrupación, ya que sabemos cuántos entrarán en cada grupo, pero ya no sabemos cuántos grupos habrá ahora.
Como sabemos que hay 4 en cada grupo, podemos agrupar 4 manzanas hasta que hayamos cubierto las 12 para ver que hay 3 grupos.
La estructura final de la división es escalable. Mientras que en la multiplicación aumentábamos un valor, la estructura de división se reducía. Por ejemplo, Shannen tiene 6 bolígrafos y Jen tiene 3 veces menos. ¿Cuántos bolígrafos tiene Jen?
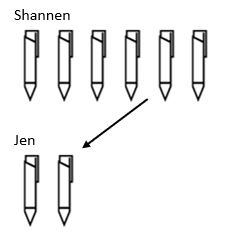
Aquí podemos ver que para encontrar la cantidad total de bolígrafos que tiene Jen, tuvimos que tomar la cantidad que tenía Shannen y disminuirla en un factor de escala de 3 para que Jen termine con 2 bolígrafos.
Por experiencia, esta es la estructura de división más difícil de comprender para los estudiantes y es una que debe revisarse junto con el escalado como multiplicación, ya que es una habilidad crucial al convertir mediciones y monedas de una cantidad mayor a una cantidad menor. Por ejemplo, Kilómetros a millas.
División Año 3
En el Plan de Estudios Nacional de matemáticas en Inglaterra, para cada área de matemáticas descrita, hay un elemento estatutario y un elemento no estatutario. El elemento estatutario es el siguiente:
- Recordar y utilizar datos de multiplicación y división para las tablas de multiplicación de 3, 4 y 8
- Escribir y calcular sentencias matemáticas para multiplicación y división utilizando las tablas de multiplicación que conozcan, incluso para números de dos dígitos por números de un dígito, utilizando métodos mentales y progresando a métodos escritos formales
- Resolver problemas, incluidos los problemas de números faltantes, que involucran multiplicación y división, incluidos los problemas de escalado de enteros positivos y los problemas de correspondencia en los que n objetos están conectados a m objetos.
Notas y orientaciones no reglamentarias:
- Los alumnos desarrollan métodos mentales eficientes, por ejemplo, utilizando la conmutatividad y la asociatividad (por ejemplo, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) y hechos de multiplicación y división (por ejemplo, usando 3 × 2 = 6, 6 ÷ 3 = 2 y 2 = 6 ÷ 3) para derivar hechos relacionados (por ejemplo, 30 × 2 = 60, 60 ÷ 3 = 20 y 20 = 60 ÷ 3).
- Los alumnos desarrollan métodos escritos fiables de multiplicación y división, comenzando con cálculos de números de dos dígitos por números de un dígito y avanzando hacia los métodos escritos formales de multiplicación y división cortas.
- Los alumnos resuelven problemas simples en contextos, decidiendo cuál de las cuatro operaciones usar y por qué. Estos incluyen contextos de medición y escalado (por ejemplo, cuatro veces más alto, ocho veces más largo, etc.).) y problemas de correspondencia en los que m objetos están conectados a n objetos (por ejemplo, 3 sombreros y 4 abrigos, ¿cuántos trajes diferentes?; 12 dulces compartidos a partes iguales entre 4 niños; 4 pasteles compartidos a partes iguales entre 8 niños).
Actividades de la División Año 3
Esto no cubrirá una lección per se, sino que proporcionará una guía sobre cómo se puede enseñar a la división con algún entendimiento conceptual en esta etapa. Un requisito previo para esto sería la enseñanza de hechos de multiplicación relacionados primero antes de enseñar cualquier división relacionada.
Al pensar en estructuras, es mejor en esta parte del viaje de aprendizaje de los estudiantes seguir agrupando y compartiendo. Para los siguientes ejemplos, veremos cómo desarrollar la comprensión de los estudiantes de dividir por 4. Seguirá el enfoque Concreto-Pictórico-Abstracto.
A menudo es la comprensión del número de los estudiantes lo que puede limitar su progreso en la división. Particularmente cuando se trata de agrupar y compartir cuando solo quitan uno continuamente del todo.
Desde el comienzo de la división de enseñanza, los maestros deben apoyarse en lo que los estudiantes ya saben sobre números pares y otros datos numéricos para avanzar a los estudiantes hacia el conteo en cualquier número que sea apropiado. Los contadores
se pueden usar para demostrar hechos de división relacionados, ya que los estudiantes habrán utilizado las tesis al construir su comprensión conceptual de la multiplicación. Preguntas como, ‘ ¿Cuántos grupos de 4 hay?¿y cuántos hay en cada grupo?»debe ser preguntado y las respuestas deben relacionarse con la forma en que esto muestra la división.
Maestra: ¿Cuántos mostradores hay?
Niño: Cuatro
Profesor: Bueno. Este es un grupo de cuatro. Cuántos grupos de cuatro hay?
Niño: Uno
Profesor: Excelente. Tenemos cuatro mostradores en un grupo. Hemos agrupado cuatro contadores en un solo grupo. ¿Qué hemos hecho?
Hijo: Agrupó cuatro contadores en un grupo.
Maestro: Brillante. Cuando agrupamos cuatro contadores en un grupo, hemos hecho el cálculo matemático de cuatro divididos por uno. ¿Qué cálculo hicimos?
Niño: Cuatro dividido por uno.
Profesor: Y cuando resolvemos cuatro dividido por uno, la respuesta es cuatro, porque hemos hecho un grupo que tiene cuatro elementos en él. Cuatro dividido por uno es cuatro. ¿Qué es cuatro dividido por uno?
Niño: Cuatro dividido por uno es cuatro.
Profesor: Excelente
Puede ver cómo se repetiría para lo siguiente:
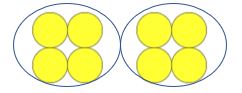
Maestra: ¿Cuántos mostradores hay?
Niño: Ocho
Maestro: Bien, este es un grupo de cuatro. Cuántos grupos de cuatro hay?
Niño: Dos
Profesor: Excelente. Tenemos cuatro mostradores en un grupo. Hemos agrupado cuatro contadores en dos grupos. ¿Qué hemos hecho?
Hijo: Agrupó cuatro contadores en dos grupos.
Maestro: Brillante. Cuando agrupamos cuatro contadores en dos grupos, hemos hecho el cálculo matemático de ocho dividido por dos. ¿Qué cálculo hicimos?
Niño: Ocho dividido por dos.
Profesor: Y cuando resolvemos ocho dividido por dos, la respuesta es cuatro porque hemos hecho dos grupos que tienen cuatro elementos en él. Ocho dividido por dos es cuatro. ¿Qué es ocho dividido por dos?
Niño: Ocho dividido por dos es cuatro.
Profesor: Excelente
Cuando los estudiantes están empezando a tener confianza con esto, podemos pasar a otros modelos como cañas Cuisenaire.

Aquí se representa la cantidad total en el tren superior y la barra púrpura (que en este caso representa 4 y si ha leído otros blogs en esta serie, con suerte sabrá cuánto soy un defensor para su uso en el aula y para que los estudiantes sean conscientes de su valor para entonces) se usa para mostrar cuántos grupos de 4 pueden entrar en la cantidad total.
Los estudiantes pueden pasar a dibujar escenarios leídos por el maestro. Por ejemplo. Hay 24 botones y deben agruparse en 4. Cuántos grupos hay? Los estudiantes podrían dibujar esos botones y agruparlos en 4, etc.
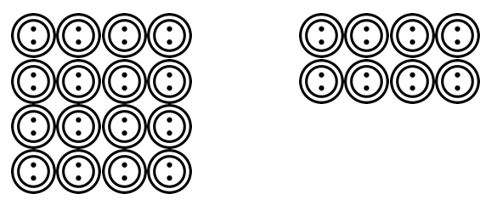
Una vez que los estudiantes se han acostumbrado a poder visualizar estos escenarios de agrupación o división compartida en una variedad de contextos, pueden pasar a representaciones más abstractas utilizando símbolos matemáticos.

3 Hojas de trabajo de División larga Para los Años 3-6
Prepare a sus alumnos para la división larga a lo largo de KS2 con estas hojas de trabajo de división larga.
Problemas verbales de división Año 3
Los problemas verbales del Año 3 usarán comúnmente la estructura de agrupación o uso compartido.
Hay 40 pasteles y 10 estudiantes. ¿Cuántos pasteles recibiría cada estudiante?
Como sabemos cuántos grupos hay (10), necesitamos calcular la cantidad por grupo, por lo que esta es una estructura para compartir. Se espera que los estudiantes usen su conocimiento de la tabla de 4 tiempos para resolver esto y obtener la respuesta 4. División
: Razonamiento y Resolución de Problemas Año 3
Para el razonamiento y la resolución de problemas, una buena actividad que encuentro es hacer coincidir un problema de palabras con un cálculo. Por ejemplo:
Haga coincidir los problemas verbales que se resuelven sabiendo 20 dividido por 4.
- Hay 20 lápices y se van a colocar en paquetes de 5. Cuántos en cada paquete?
- Había 20 lápices y luego un estudiante trae 4 más. Cuántos lápices hay ahora?
- Hay 20 lápices y se van a colocar en paquetes de 4. Cuántos en cada paquete?
- Había 20 lápices y luego desaparecieron 4. Cuántos lápices hay ahora?
Conseguir que los estudiantes escriban sus explicaciones para cada pregunta es útil, ya que permite ver su forma de pensar. Las preguntas se han seleccionado cuidadosamente para que los números de cada pregunta se relacionen con los números de la pregunta, de modo que los estudiantes confíen en sus habilidades matemáticas para deducir la respuesta correcta.
División Año 4
En el Plan de Estudios Nacional de matemáticas en Inglaterra, para cada área de matemáticas descrita, hay un elemento estatutario y un elemento no estatutario. El elemento estatutario es el siguiente:
- Recordar datos de multiplicación y división para tablas de multiplicación de hasta 12 × 12
- Usar valores de posición, datos conocidos y derivados para multiplicar y dividir mentalmente, incluidos: multiplicar por 0 y 1; dividir por 1; multiplicar tres números
Notas y directrices no reglamentarias:
- Los alumnos continúan practicando el recordar y el uso de tablas de multiplicar y datos de división relacionados para ayudar a la fluidez.
- Los alumnos practican métodos mentales y los amplían a números de tres dígitos para obtener hechos (por ejemplo, 600 ÷ 3 = 200 puede derivarse de 2 x 3 = 6).
- Los alumnos practican para dominar el método formal escrito de multiplicación y división cortas con respuestas exactas
- Los alumnos resuelven problemas de dos pasos en contextos, eligiendo la operación adecuada, trabajando con números cada vez más difíciles. Esto debe incluir preguntas de correspondencia, como el número de opciones de una comida en un menú, o tres pasteles compartidos por igual entre 10 niños.
Ideas de lecciones de División Año 4
Para esta lección, veré cómo puede comenzar a enseñar división corta usando manipulativos junto a ella.
Digamos que vamos a enseñar a los estudiantes división corta para la pregunta 168 dividida por 12.
Normalmente escribiríamos esto en lo que comúnmente se conoce como parada de autobús. Pero lo interesante es que en diferentes lugares del mundo lo escriben de manera diferente.
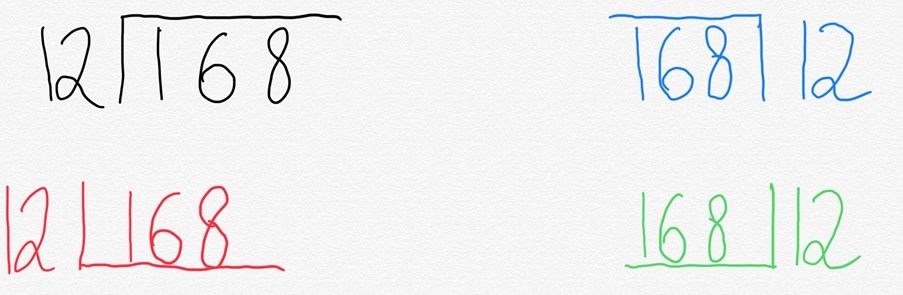
La razón de esto es bastante simple. Lo que en realidad representa la «parada de autobús» es una forma abreviada de representar un rectángulo.
Cuando enseñamos la división corta formal, lo que efectivamente decimos es que necesitas imaginar un rectángulo donde el ancho sea 12. El área total del rectángulo es de 168 y estamos tratando de encontrar la longitud que falta en la parte superior. Entonces, ¿cómo mostramos esto usando manipulativos? Los bloques de Dienes son una herramienta útil para esto.
Sabemos que la cantidad total es de 168. Así que necesitamos reunir 168 dienos usando la menor cantidad de bloques posible. Esto se muestra a continuación.
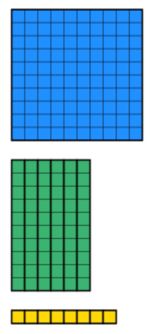
Mirando hacia atrás a la pregunta, sabemos que el ancho es 12. Eso significa que ahora necesitamos manipular los bloques para obtener un ancho de 12. Tenga en cuenta que el rectángulo debe ser sólido y no puede faltar partes. Por ejemplo, lo siguiente no se permitiría a pesar de que hay 12 unidades que bajan por el ancho.
En su lugar, los estudiantes pueden rotar dos bloques de 10s para obtener lo siguiente. Observe cómo hay 12 en cada columna y es un objeto sólido.
La parte final que los estudiantes deben hacer es usar los bloques restantes para crear un rectángulo vendido manteniendo el ancho 12. Esto podría llevar algún tiempo, pero con la práctica, los estudiantes se vuelven más rápidos. Después de algún tiempo, los estudiantes producirán esto:
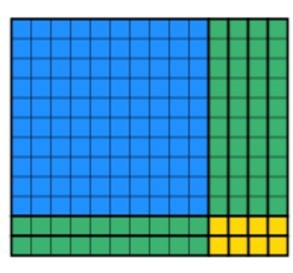
Podemos ver que los 168 bloques se han agotado y que el ancho sigue siendo 12. Para encontrar la respuesta, los estudiantes deben contar la longitud, que en este caso es 14. He superpuesto ambos métodos a continuación para que pueda ver cómo se complementan entre sí a continuación.
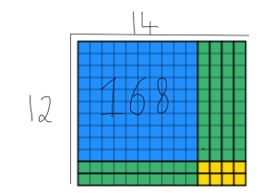
Esta es una estrategia útil para enseñar a los estudiantes en Year 4, ya que hay repercusiones masivas en otras áreas del currículo que ya se iluminan para los estudiantes.
Aunque es posible que aún no lo reconozcan, al enseñar división corta como esta, ya se les ha introducido en el perímetro y el área, piense en cuánto tiempo de enseñanza se puede ahorrar cuando se realiza esta conexión. No solo eso, sino que, en segundo lugar, este enfoque se transfiere al pensamiento algebraico.
Problemas verbales de división Año 4
Se esperaría que los estudiantes aprovecharan su conocimiento del valor del lugar para resolver problemas basados en divisiones y, por lo tanto, sería un problema verbal apropiado.
Un huerto cultivado 4,800 manzanas en una temporada. Se colocan en paquetes de 4 antes de salir al mercado. Cuántos paquetes hay?
Aquí los estudiantes deben usar el hecho de que 4 x 12 = 48 y como 4,800 es cien veces más que 48, 12 también debe multiplicarse por 100 para obtener 1,200
División: Razonamiento y Resolución de Problemas Año 4
¿Es siempre, a veces o nunca cierto que la suma de tres números pares es divisible por 4?
Esta pregunta da a los estudiantes una amplia oportunidad de experimentar dentro de los parámetros de la pregunta. Los estudiantes que necesitan más apoyo pueden mirar los números pares de sing digit y los estudiantes pueden subir a lo que se sientan cómodos.
Con preguntas abiertas como esta, es bueno proporcionar un requisito mínimo para cuántos intentos deben hacer los estudiantes, de lo contrario, a menudo elegirán hacer el mínimo.
La respuesta a esta pregunta es a veces.
Un truco rápido para saber si un número es divisible es mirar los últimos 2 dígitos del número y ver si son divisibles por 4. Por ejemplo, si un niño encontró la suma de 34, 36 y 38 y obtuvo 108, como maestro sé que este número es divisible por 4, ya que los dos dígitos finales (08) hacen 8 y son divisibles por 4. Si un niño eligió 34, 36 y 48 para obtener 118, sé que esto no es divisible por 4, ya que 18 – los dos últimos dígitos de 118 – no son divisibles por 4.
División Year 5
En el Plan de Estudios Nacional de matemáticas en Inglaterra, para cada área de matemáticas descrita, hay un elemento estatutario y un elemento no estatutario. El elemento estatutario es el siguiente:
- Multiplicar y dividir números basándose mentalmente en hechos conocidos
- Dividir números de hasta 4 dígitos por un número de un dígito utilizando el método escrito formal de división corta e interpretar los restos apropiadamente para el contexto
- Multiplicar y dividir números enteros y aquellos que involucran decimales por 10, 100 y 1000
- Resolver problemas que involucran multiplicación y división, incluyendo el uso de su conocimiento de factores y múltiplos, cuadrados y cubos
- Resuelven problemas que implican suma, resta, multiplicación y división y una combinación de estos, incluida la comprensión del significado del signo igual
- , resuelven problemas que involucran multiplicación y división, incluida la escala por fracciones simples y problemas que involucran tasas simples.
Notas y orientaciones no reglamentarias:
- Los alumnos interpretan las respuestas no enteras a la división expresando los resultados de diferentes maneras según el contexto, incluso con restos, como fracciones, decimales o redondeando (por ejemplo, 98 ÷ 4 = = 24 r 2 = 24 = 24.5 ≈ 25).
- Los alumnos utilizan la multiplicación y la división como inversas para apoyar la introducción de la relación en el año 6, por ejemplo, multiplicando y dividiendo por potencias de 10 en dibujos a escala o multiplicando y dividiendo por potencias de 1.000 en la conversión entre unidades, como kilómetros y metros.
Actividades de la División Año 5
La División en el Año 5 progresa mediante el uso de restos en las respuestas. Para esta lección, miraré otros manipulativos de uso que los maestros pueden usar para enseñar la división de 4 por 1 dígito.
Si la pregunta fuera 5,642 dividida por 4, podríamos representar esto usando un gráfico de valor posicional y contadores de valor posicional como podemos ver a continuación.
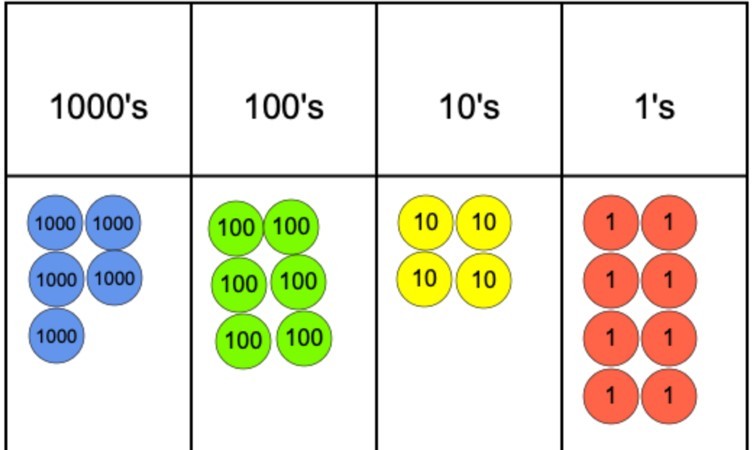
El siguiente paso sería comenzar a agrupar los contadores en 4, ya que este es nuestro divisor. Sin embargo, como se puede ver, rápidamente llegamos a un problema en la columna de los 1000, ya que podemos agrupar 4 de los contadores, pero luego no podemos agrupar el contador restante en un grupo de 4.
Para combatir este problema, el contador de 1000 que no se ha agrupado se puede cambiar por diez contadores de 100. Estos se pueden agrupar en grupos de 4 y esto puede suceder sin que queden contadores de 100s. A partir de ahí, es un simple caso de pasar a los 10 y finalmente a los unos.
Como hay nueve contadores 1s, podemos agrupar 8 de ellos en 2 grupos y 4 y afirmar que queda uno*. Para encontrar la respuesta, todo lo que se requiere es contar el número de grupos realizados en cada valor de posición y usarlos para escribir los dígitos para crear la respuesta final. En este caso, la respuesta sería 1,412 resto 1.
* Cuando esté mirando decimales, puede cambiar el contador 1s restante por diez contadores 0.1 y continuar con la división como se describió anteriormente. Es útil que los estudiantes estén familiarizados con este modelo, ya que puede ayudar a desmitificar la división con decimales con los que los estudiantes pueden luchar. Esto les ayuda a ver que es una continuación de un proceso con el que ya están familiarizados en lugar de algo nuevo.
Problemas de división Year 5
Al dividir en Year 5, los estudiantes encontrarán escenarios en los que necesitarán redondear su respuesta para que la respuesta tenga sentido en el contexto. Una pregunta apropiada que demuestra esto sería algo como lo siguiente:
Una escuela está planeando una discoteca social distante donde planean ofrecer 250 ml de jugo a cada estudiante. Pueden comprar botellas de jugo de 2 litros. Esperan que lleguen 33 estudiantes, así que sepan que darán 8,25 litros de jugo. ¿Cuántas botellas de jugo necesitarán comprar?
Una respuesta común es que los estudiantes dirán 4 y cuarto. Sin embargo, como no se puede comprar un cuarto de botella, en este caso la respuesta correcta sería que se necesitarían 5 botellas de jugo para garantizar que todos los estudiantes pudieran participar.
División: Razonamiento y Resolución de problemas Year 5
Como se señaló anteriormente, en Year 5, los estudiantes encontrarán escenarios dentro de la división en los que se les pedirá que elijan si una respuesta debe redondearse hacia arriba o hacia abajo. Por ejemplo, cuando una pregunta pide a los estudiantes que calculen cuántos autobuses se necesitan para un viaje escolar.
Hacer que los estudiantes creen sus propios problemas usando un rango de contexto proporcionado puede ser una actividad realmente desafiante que hace que los estudiantes piensen matemáticamente sobre el contexto y la división.
Los estudiantes pueden intercambiar estas preguntas que han creado con un compañero y luego ir a resolverlas y verificar con el creador de la pregunta original si tienen la respuesta correcta.
División Year 6
En el Plan de Estudios Nacional de matemáticas en Inglaterra, para cada área de matemáticas descrita, hay un elemento estatutario y un elemento no estatutario. El elemento estatutario es el siguiente:
- divida números de hasta 4 dígitos por un número entero de dos dígitos utilizando el método escrito formal de división larga, e interprete los restos como restos de números enteros, fracciones o redondeando, según corresponda para el contexto
- divida números de hasta 4 dígitos por un número de dos dígitos utilizando el método escrito formal de división corta, cuando proceda, interpretando los restos de acuerdo con el contexto
- realice cálculos mentales, incluso con operaciones mixtas y de gran tamaño números
- identificar factores comunes, múltiplos comunes y números primos
- utilizar su conocimiento del orden de operaciones para llevar a cabo cálculos relativos a las cuatro operaciones
Notas y orientaciones no reglamentarias:
- Resolver problemas de suma, resta, multiplicación y división
- Utilice la estimación para verificar las respuestas a los cálculos y determinar, en el contexto de un problema, un grado de precisión adecuado.
Ideas de lecciones de División Year 6
Sophie Bartlett (@_MissieBee) ha creado un excelente blog aquí (enlace al blog de Sophie sobre enseñar división larga) que detalla cómo enseñaría división larga durante una clase de year 6. Como la división larga es el único aprendizaje nuevo en división para Year 6, esta es una forma ideal de introducir el procedimiento de la división larga.
Preguntas de división Year 6
Un problema típico de palabras de división que un estudiante de Year 6 encontraría sería:
Una escuela recaudó £3,146 de una venta de pasteles. asistieron al evento 104 padres de familia. Si todos los padres gastaron la misma cantidad de dinero, ¿cuánto gastó cada uno de ellos?
Aquí, se espera que los estudiantes utilicen el método de división larga para resolver esta pregunta y obtener la respuesta £30.25.
División: Razonamiento y Resolución de problemas Año 6
Con algo procedimental como la división larga, una buena actividad de razonamiento es hacer que los estudiantes encuentren errores. Estos recursos constituyen un gran banco de actividades de este tipo. Como podemos ver en la pregunta de abajo, los estudiantes han hecho todo el trabajo duro, pero un error descuidado al contar los grupos de 59 significa que el niño creía que 59 x 7 era 472 y no 59 x 8.
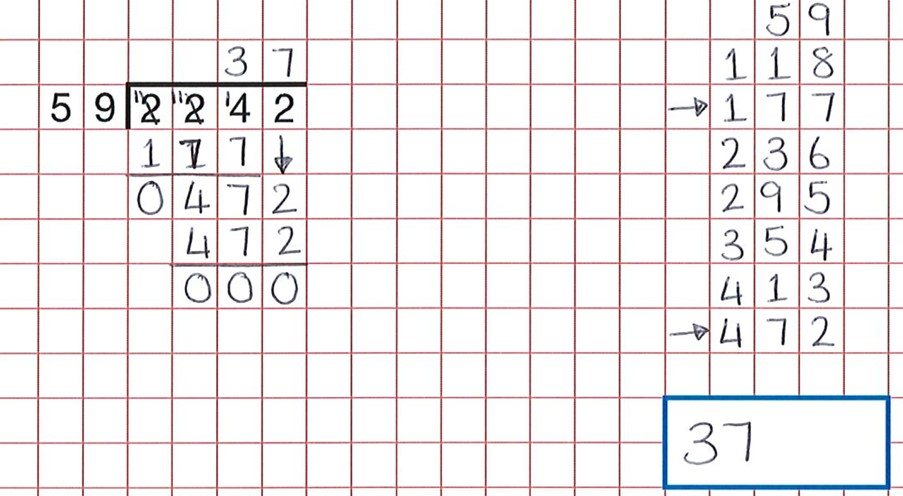
La respuesta correcta habría sido 38.
La división es un tema clave de matemáticas, no solo en KS2, sino en matemáticas en su conjunto. Espero que este post te haya dado algunas buenas ideas para ayudar a tus alumnos a abordarlo con confianza.
Lecciones de matemáticas en línea 1 a 1 en las que confían escuelas y maestros
Cada semana, los tutores especialistas en matemáticas de Third Space Learning apoyan a miles de niños de escuela primaria con lecciones semanales en línea 1 a 1 e intervenciones de matemáticas. Desde 2013 hemos ayudado a más de 100.000 niños a convertirse en matemáticos más seguros y capaces. Obtenga más información o solicite un presupuesto personalizado para hablar con nosotros sobre sus necesidades y cómo podemos ayudarlo.
La enseñanza primaria se orienta a las necesidades de cada niño y sigue de cerca el Plan de estudios nacional.