La Division de l’Étape Clé 2 constitue la dernière partie des « Quatre Opérations » – les quatre concepts mathématiques fondamentaux que les élèves doivent connaître. Ce blog vous aidera à vous assurer que tous vos élèves, de la 3e à la 6e année, peuvent aborder la division avec la confiance dont ils ont besoin pour réussir.
La division en mathématiques KS2 s’appuie sur ce qui a été appris à KS1. À la fin de l’année 2, les élèves à la norme attendue seront en mesure de « rappeler et d’utiliser les faits de multiplication et de division pour les tables de multiplication 2, 5 et 10, y compris la reconnaissance des nombres pairs et impairs. »
Pour les enseignants de la 3e année, il est toujours judicieux de s’assurer que les élèves les connaissent très bien. Par là, je ne veux pas simplement dire qu’ils peuvent vous décrire les faits de division, mais ils comprennent vraiment comment représenter ces faits à la fois avec des représentations concrètes, des explications verbales et par d’autres méthodes picturales.
Les élèves qui ne sont pas capables de le faire, mais qui sont capables de vous raconter verbalement les faits de la division, ont une compréhension très superficielle de la division et pour qu’ils puissent progresser dans des activités de résolution de problèmes plus difficiles, approfondir leur compréhension conceptuelle de la division est un must à l’année 3.
Le Programme national place la division dans la même section que la multiplication pour les années 3 à 5 et la place dans une section appelée « Quatre opérations » en année 6. Les parties du Programme national ne concernent que celles qui mentionnent spécifiquement la division. Les autres éléments de ces sections peuvent être trouvés dans le blog sur la multiplication ou l’addition et la soustraction le cas échéant.
Qu’Est-Ce Que La Division ?
La division est l’une des quatre opérations – les quatre concepts mathématiques fondamentaux que les élèves doivent connaître – aux côtés de l’addition et de la soustraction et de la multiplication.
Où la multiplication combine un nombre plusieurs fois, la division est l’inverse: déterminer combien de fois un nombre est contenu dans un autre. Par exemple, diviser 10 par 2, c’est demander combien de fois 2 est contenu dans 10.

des interventions mathématiques en ligne de Third Space Learning.
Division d’enseignement KS2 – La théorie
La division est l’inverse de la multiplication. Comme pour le blog de multiplication, l’enseignement de la division contient trois structures sous-jacentes qui, associées aux faits de division et à la compréhension conceptuelle, donneront aux étudiants la meilleure opportunité de réussir lorsqu’ils résolvent des problèmes liés à la division.
Les trois structures sont le partage, le regroupement et la mise à l’échelle. Bien qu’il n’y ait pas assez de temps pour les explorer en profondeur, ce qui suit ne sera qu’une courte introduction à eux.
Le partage et le regroupement sont l’inverse de la multiplication comme addition répétée. Le partage est un concept structurel introduit dans KS1 et plus tôt où, comme son nom l’indique, un montant est partagé en groupes égaux.
Par exemple, 12 pommes sont partagées entre 3 élèves. Combien de pommes chaque élève reçoit-il? Ici, nous connaissons le montant total (12 pommes) et, surtout, nous savons comment nous allons partager le montant (3). Selon l’endroit où les étudiants se trouvent dans leur parcours mathématique, ils peuvent soustraire à plusieurs reprises un certain nombre (1, 2, 3 ou 4) du montant en trois piles qui représentent les trois étudiants.
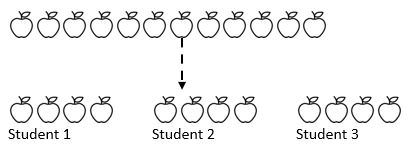
Comme nous pouvons le voir ci-dessus, le montant total a été partagé en trois groupes égaux.
Le regroupement est similaire au partage, mais ce que nous savons est légèrement différent du partage. Dans la structure de partage, nous connaissons le nombre de groupes que le partage aura lieu. Dans la structure de regroupement, nous connaissons le montant dans chaque groupe mais pas le nombre de groupes réels qu’il y a.
Par exemple, 12 pommes sont partagées en groupes de 4. Combien de groupes y aura-t-il? Bien que cette question soit très similaire à celle ci-dessus, elle prend maintenant en compte la structure de regroupement, car nous savons combien iront dans chaque groupe, mais nous ne savons plus combien de groupes il y en aura maintenant.
Comme nous savons qu’il y en a 4 dans chaque groupe, nous pouvons regrouper 4 pommes jusqu’à ce que nous ayons couvert les 12 pour voir qu’il y a 3 groupes.
La structure finale de la division est la mise à l’échelle. Alors que dans la multiplication, nous augmentions une valeur, la structure de division diminue. Par exemple, Shannen a 6 stylos et Jen en a 3 fois moins. Combien de stylos Jen a-t-elle?
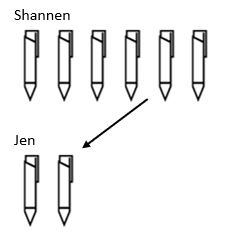
Ici, nous pouvons voir que pour trouver la quantité totale de stylos que Jen a, nous avons dû prendre la quantité que Shannen avait et la diminuer d’un facteur d’échelle de 3 pour que Jen se retrouve avec 2 stylos.
D’après l’expérience, il s’agit de la structure de division la plus difficile à saisir et à comprendre pour les étudiants et qui doit être revisitée en conjonction avec la mise à l’échelle en tant que multiplication car il s’agit d’une compétence cruciale lors de la conversion de mesures et de devises d’une plus grande quantité à une plus petite quantité. Par exemple, Kilomètres en miles.
Division Année 3
Dans le Programme national de mathématiques en Angleterre, pour chaque domaine de mathématiques décrit, il y a à la fois un élément statutaire et un élément non statutaire. L’élément statutaire est le suivant:
- Rappeler et utiliser les faits de multiplication et de division pour les tables de multiplication à 3, 4 et 8
- Écrire et calculer des énoncés mathématiques pour la multiplication et la division en utilisant les tables de multiplication qu’ils connaissent, y compris pour les nombres à deux chiffres fois les nombres à un chiffre, en utilisant des méthodes écrites mentales et progressives
- Résoudre des problèmes, y compris des problèmes de nombres manquants, impliquant la multiplication et la division, y compris des problèmes de mise à l’échelle d’entiers positifs et des problèmes de correspondance dans lesquels n objets sont connectés à m objets.
Notes et directives non statutaires:
- Les élèves développent des méthodes mentales efficaces, par exemple en utilisant la commutativité et l’associativité (par exemple, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) et les faits de multiplication et de division (par exemple, en utilisant 3 × 2 = 6, 6 ÷ 3 = 2 et 2 = 6 ÷ 3) pour dériver des faits connexes (par exemple, 30 × 2 = 60, 60 ÷ 3 = 20 et 20 = 60 ÷ 3).
- Les élèves développent des méthodes écrites fiables pour la multiplication et la division, en commençant par des calculs de nombres à deux chiffres par des nombres à un chiffre et en progressant vers les méthodes écrites formelles de multiplication et de division courtes.
- Les élèves résolvent des problèmes simples dans des contextes, décidant laquelle des quatre opérations utiliser et pourquoi. Il s’agit notamment de contextes de mesure et de mise à l’échelle (par exemple, quatre fois plus élevés, huit fois plus longs, etc.) et des problèmes de correspondance dans lesquels m objets sont connectés à n objets (par exemple, 3 chapeaux et 4 manteaux, combien de tenues différentes?; 12 bonbons partagés à parts égales entre 4 enfants; 4 gâteaux partagés à parts égales entre 8 enfants).
Activités de division Année 3
Cela ne couvrira pas une leçon en soi, mais fournira un guide sur la façon dont la division peut être enseignée avec une certaine compréhension conceptuelle à ce stade. Une condition préalable pour cela serait l’enseignement des faits de multiplication connexes avant d’enseigner toute division connexe.
Lorsqu’on pense aux structures, il est préférable, dans cette partie du parcours d’apprentissage des élèves, de s’en tenir au regroupement et au partage. Pour les exemples suivants, nous examinerons le développement de la compréhension par les élèves de la division par 4. Il suivra l’approche Concrète-Picturale-Abstraite.
C’est souvent la compréhension du nombre par les élèves qui peut limiter leurs progrès en division. En particulier lorsqu’il s’agit de regrouper et de partager lorsqu’ils n’en retirent qu’un en continu de l’ensemble.
Dès le début de la division de l’enseignement, les enseignants doivent s’appuyer sur ce que les élèves savent déjà des nombres pairs et d’autres faits sur les nombres pour faire progresser les élèves sur le comptage dans le nombre approprié.
Les compteurs peuvent être utilisés pour démontrer des faits de division connexes, car les étudiants auront utilisé des thèses lors de la construction de leur compréhension conceptuelle de la multiplication. Des questions telles que: « Combien y a-t-il de groupes de 4? » et » Combien y en a-t-il dans chaque groupe? »devrait être demandé et les réponses devraient porter sur la façon dont cela montre la division.
Professeur : Combien y a-t-il de compteurs?
Enfant: Quatre
Enseignant: Bien. C’est un groupe de quatre. Combien y a-t-il de groupes de quatre?
Enfant: Un
Enseignant: Excellent. Nous avons quatre compteurs dans un groupe. Nous avons regroupé quatre compteurs en un seul groupe. Qu’avons-nous fait?
Enfant : Regroupé quatre compteurs en un seul groupe.
Professeur: Brillant. Lorsque nous regroupons quatre compteurs en un seul groupe, nous avons fait le calcul mathématique de quatre divisés par un. Quel calcul avons-nous fait?
Enfant: Quatre divisé par un.
Enseignant: Et lorsque nous résolvons quatre divisés par un, la réponse est quatre parce que nous avons créé un groupe contenant quatre éléments. Quatre divisé par un est quatre. Qu’est-ce que quatre divisés par un?
Enfant: Quatre divisé par un est quatre.
Professeur: Excellent
Vous pouvez voir comment cela serait répété pour ce qui suit:
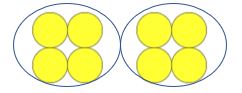
Professeur : Combien y a-t-il de compteurs?
Enfant: Huit
Enseignant: Bien, c’est un groupe de quatre. Combien y a-t-il de groupes de quatre?
Enfant: Deux
Enseignant: Excellent. Nous avons quatre compteurs dans un groupe. Nous avons regroupé quatre compteurs en deux groupes. Qu’avons-nous fait?
Enfant : Regroupé quatre compteurs en deux groupes.
Professeur: Brillant. Lorsque nous regroupons quatre compteurs en deux groupes, nous avons fait le calcul mathématique de huit divisés par deux. Quel calcul avons-nous fait?
Enfant: Huit divisé par deux.
Enseignant: Et lorsque nous résolvons huit divisés par deux, la réponse est quatre parce que nous avons créé deux groupes contenant quatre éléments. Huit divisé par deux est quatre. Qu’est-ce que huit divisé par deux?
Enfant: Huit divisé par deux est quatre.
Professeur: Excellent
Lorsque les étudiants commencent à avoir confiance en cela, nous pouvons passer à d’autres modèles tels que les cannes Cuisenaire.

Ici, le montant total est représenté dans le train supérieur et la tige violette (qui dans ce cas représente 4 et si vous avez lu d’autres blogs dans cette série, j’espère que vous saurez à quel point je suis un défenseur de leur utilisation en classe et que les étudiants seront conscients de sa valeur d’ici là) est utilisée pour montrer combien de groupes de 4 peuvent entrer dans le montant total.
Les élèves peuvent ensuite élaborer des scénarios lus par l’enseignant. Exemple. Il y a 24 boutons et ils doivent être regroupés en 4. Combien y a-t-il de groupes ? Les élèves pourraient dessiner ces boutons et les regrouper en 4, etc.
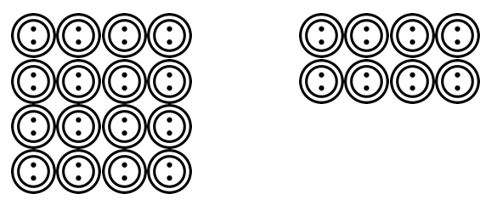
Une fois que les élèves se sont habitués à pouvoir visualiser ces scénarios de regroupement ou de partage de divisions dans une gamme de contextes, ils peuvent passer à des représentations plus abstraites à l’aide de symboles mathématiques.

3 Feuilles de travail à division longue Pour les années 3-6
Préparez vos élèves à une division longue tout au long de la KS2 avec ces feuilles de travail à division longue.
Problèmes de mots de division Année 3
Les problèmes de mots de l’année 3 utiliseront généralement la structure de regroupement ou de partage.
Il y a 40 gâteaux et 10 étudiants. Combien de gâteaux chaque élève obtiendrait-il?
Comme nous savons combien de groupes il y a (10), nous devons calculer le montant par groupe, il s’agit donc d’une structure de partage. Les étudiants devraient utiliser leurs connaissances du tableau des temps 4 pour résoudre ce problème et obtenir la réponse 4.
Division: Raisonnement et Résolution de problèmes Année 3
Pour le raisonnement et la résolution de problèmes, une bonne activité que je trouve est de faire correspondre un problème de mot à un calcul. Par exemple:
Faites correspondre les problèmes de mots qui sont résolus en connaissant 20 divisé par 4.
- Il y a 20 crayons et ils vont être placés en paquets de 5. Combien dans chaque paquet?
- Il y avait 20 crayons et un étudiant en apporte 4 de plus. Combien y a-t-il de crayons maintenant?
- Il y a 20 crayons et ils vont être placés en paquets de 4. Combien dans chaque paquet?
- Il y avait 20 crayons, puis 4 ont disparu. Combien y a-t-il de crayons maintenant?
Amener les élèves à écrire leurs explications pour chaque question est utile car cela permet de voir leur pensée. Les questions ont été sélectionnées avec soin afin que les nombres de chaque question soient liés aux nombres de la question afin que les élèves se fient à leurs compétences mathématiques pour en déduire la bonne réponse.
Année de division 4
Dans le Programme national de mathématiques en Angleterre, pour chaque domaine de mathématiques décrit, il y a à la fois un élément statutaire et un élément non statutaire. L’élément statutaire est le suivant:
- Rappeler les faits de multiplication et de division pour les tables de multiplication jusqu’à 12 × 12
- Utilisez la valeur de la place, les faits connus et dérivés pour multiplier et diviser mentalement, y compris: multiplier par 0 et 1; diviser par 1; multiplier ensemble trois nombres
Notes et directives non statutaires:
- Les élèves continuent de s’exercer à rappeler et à utiliser les tables de multiplication et les faits de division connexes pour faciliter la fluidité.
- Les élèves pratiquent des méthodes mentales et les étendent à des nombres à trois chiffres pour dériver des faits (par exemple, 600 ÷ 3 = 200 peut être dérivé de 2 x 3 = 6).
- Les élèves s’entraînent à maîtriser la méthode écrite formelle de multiplication courte et de division courte avec des réponses exactes
- Les élèves résolvent des problèmes en deux étapes dans des contextes, en choisissant l’opération appropriée, en travaillant avec des nombres de plus en plus difficiles. Cela devrait inclure des questions de correspondance telles que le nombre de choix d’un repas sur un menu, ou trois gâteaux partagés à parts égales entre 10 enfants.
Idées de leçon de division Année 4
Pour cette leçon, je vais regarder comment vous pouvez commencer à enseigner la division courte en utilisant des manipulateurs à côté.
Disons que nous allons enseigner aux élèves une courte division pour la question 168 divisée par 12.
Nous écririons normalement ceci dans ce qui est communément appelé arrêt de bus. Mais ce qui est intéressant, c’est que différents endroits dans le monde l’écrivent différemment.
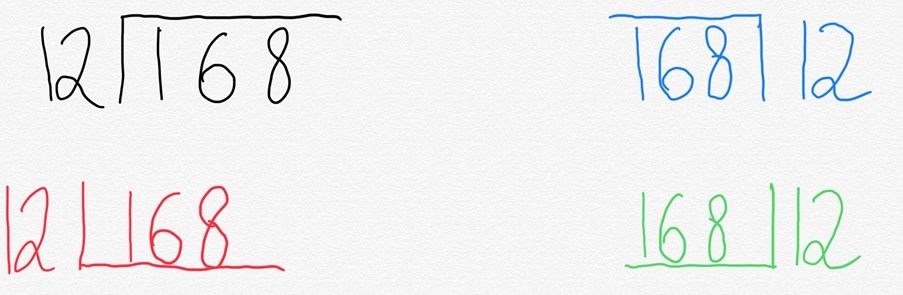
La raison en est assez simple. Ce que représente réellement « l’arrêt de bus » est une manière raccourcie de représenter un rectangle.
Lorsque nous enseignons la division courte formelle, ce que nous disons effectivement, c’est que vous devez imaginer un rectangle dont la largeur est de 12. La superficie totale du rectangle est de 168 et nous essayons de trouver la longueur manquante en haut. Alors, comment montrons-nous cela en utilisant des manipulatifs? Les blocs de diènes sont un outil utile pour cela.
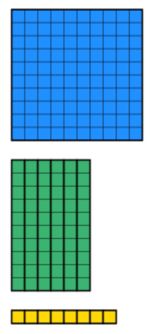
Nous savons que le montant total est de 168. Nous devons donc rassembler 168 diènes en utilisant les plus petites quantités de blocs possibles. Ceci est illustré ci-dessous.
En regardant en arrière la question, nous savons que la largeur est de 12. Cela signifie que nous devons maintenant manipuler les blocs pour obtenir une largeur de 12. Notez que le rectangle doit être solide et ne peut pas avoir de parties manquantes. Par exemple, le ci-dessous ne serait pas autorisé malgré le fait qu’il y ait 12 unités descendant sur la largeur.
Au lieu de cela, les étudiants peuvent faire pivoter deux blocs 10s pour obtenir ce qui suit. Remarquez qu’il y en a 12 dans chaque colonne et qu’il s’agit d’un objet solide.
La dernière partie que les étudiants doivent faire est d’utiliser les blocs restants pour créer un rectangle vendu tout en gardant la largeur 12. Cela pourrait prendre un certain temps, mais avec la pratique, les étudiants deviennent plus rapides. Après un certain temps, les étudiants produiront ceci:
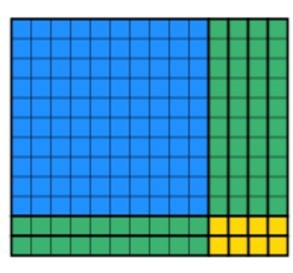
Nous pouvons voir que les 168 blocs ont été utilisés et que la largeur est toujours de 12. Pour trouver la réponse, les étudiants doivent compter la longueur, qui dans ce cas est de 14. J’ai superposé les deux méthodes ci-dessous afin que vous puissiez voir comment elles se complètent ci-dessous.
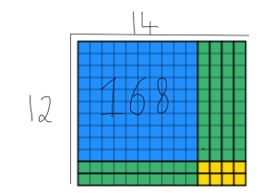
C’est une stratégie utile pour enseigner aux étudiants en 4e année car il y a des répercussions massives dans d’autres domaines du programme qui sont déjà éclairés pour les étudiants.
Bien qu’ils ne le reconnaissent peut–être pas encore, en enseignant une division courte comme celle-ci, ils ont déjà été initiés au périmètre et à la zone – pensez à combien de temps d’enseignement peut être économisé lorsque cette connexion est établie. Non seulement cela, mais au secondaire, cette approche se transfère à la pensée algébrique.
Problèmes de mots de division Année 4
Les élèves devraient tirer parti de leurs connaissances de la valeur du lieu pour résoudre des problèmes basés sur la division et un problème de mots approprié serait donc.
Un verger cultivait 4 800 pommes en une saison. Ils sont placés en paquets de 4 avant d’aller au marché. Combien y a-t-il de packs ?
Ici, les étudiants doivent utiliser le fait que 4 x 12 = 48 et que 4 800 est cent fois plus que 48, 12 doit également être multiplié par 100 pour obtenir 1 200
Division: Raisonnement et résolution de problèmes Année 4
Est-il toujours, parfois ou jamais vrai que la somme de trois nombres pairs est divisible par 4?
Cette question donne aux élèves amplement l’occasion d’expérimenter dans les paramètres de la question. Les étudiants qui ont besoin de plus de soutien peuvent regarder chanter des chiffres pairs et les étudiants peuvent aller jusqu’à tout ce avec quoi ils se sentent à l’aise.
Avec des questions ouvertes comme celle-ci, il est bon de fournir une exigence minimale pour le nombre de tentatives que les étudiants devraient faire sinon ils choisiront souvent de faire le strict minimum.
La réponse à cette question est parfois.
Une astuce rapide pour savoir si un nombre est divisible consiste à regarder les 2 derniers chiffres du nombre et à voir s’ils sont divisibles par 4. Par exemple, si un enfant trouve la somme de 34, 36 et 38 et obtient 108, en tant qu’enseignant, je sais que ce nombre est divisible par 4 car les deux derniers chiffres (08) font 8 et sont divisibles par 4. Si un enfant a choisi 34, 36 et 48 pour obtenir 118, je sais que ce n’est pas divisible par 4 car 18 – les deux derniers chiffres de 118 – ne sont pas divisibles par 4.
Année de division 5
Dans le Programme national de mathématiques en Angleterre, pour chaque domaine de mathématiques décrit, il y a à la fois un élément statutaire et un élément non statutaire. L’élément statutaire est le suivant:
- Multiplier et diviser mentalement des nombres en s’appuyant sur des faits connus
- Diviser des nombres jusqu’à 4 chiffres par un nombre à un chiffre en utilisant la méthode écrite formelle de division courte et interpréter les restes de manière appropriée pour le contexte
- Multiplier et diviser des nombres entiers et ceux impliquant des décimales par 10, 100 et 1000
- Résoudre des problèmes impliquant la multiplication et la division, y compris en utilisant leur connaissance des facteurs et les multiples, carrés et cubes
- résolvent des problèmes impliquant l’addition, la soustraction, la multiplication et la division et une combinaison de ceux-ci, y compris la compréhension de la signification du signe égal
- résolvent des problèmes impliquant la multiplication et la division, y compris la mise à l’échelle par des fractions simples et des problèmes impliquant des taux simples.
Notes et directives non statutaires:
- Les élèves interprètent les réponses non entières à la division en exprimant les résultats de différentes manières selon le contexte, y compris avec les restes, sous forme de fractions, de décimales ou en arrondissant (par exemple, 98 ÷ 4 == 24 r 2 = 24 = 24,5 ≈ 25).
- Les élèves utilisent la multiplication et la division comme des inverses pour soutenir l’introduction du rapport en 6e année, par exemple en multipliant et divisant par des puissances de 10 dans les dessins à l’échelle ou en multipliant et divisant par des puissances de 1 000 dans la conversion entre des unités telles que les kilomètres et les mètres.
Activités de division Année 5
La division de l’année 5 progresse grâce à l’utilisation de restes dans les réponses. Pour cette leçon, je vais examiner une autre utilisation des manipulateurs que les enseignants peuvent utiliser pour enseigner la division à 4 par 1 chiffres.
Si la question était 5 642 divisée par 4, nous pourrions la représenter à l’aide d’un graphique de valeurs de lieu et de compteurs de valeurs de lieu comme nous pouvons le voir ci-dessous.
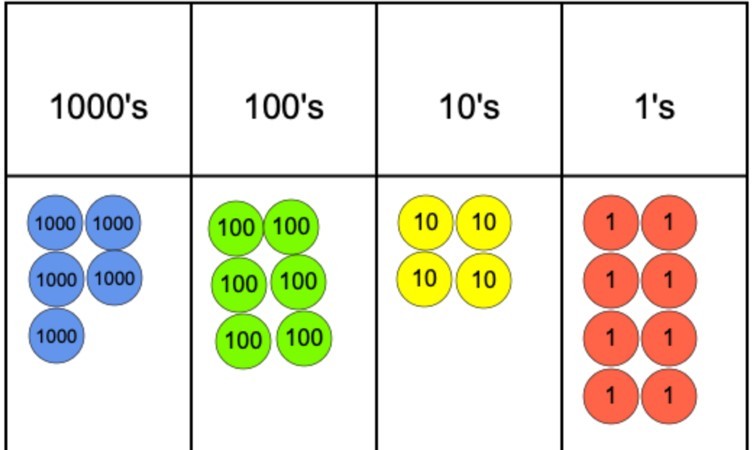
L’étape suivante serait de commencer à regrouper les compteurs en 4 car c’est notre diviseur. Cependant, comme on peut le voir, nous arrivons rapidement à un problème dans la colonne des 1000 car nous pouvons regrouper 4 des compteurs mais nous ne pouvons pas regrouper le compteur restant dans un groupe de 4.
Pour lutter contre ce problème, le compteur 1000 qui n’a pas été groupé peut être échangé contre dix compteurs 100. Ceux-ci peuvent ensuite être regroupés en groupes de 4 et cela peut se produire sans qu’il reste de compteurs 100s. De là, il s’agit d’un simple cas de passage ensuite aux 10 et enfin aux.
Comme il y a neuf compteurs 1s, nous pouvons en regrouper 8 en 2 groupes et 4 et affirmer qu’il en reste un *. Pour trouver la réponse, il suffit de compter le nombre de groupes créés dans chaque valeur de lieu et de les utiliser pour écrire les chiffres pour créer la réponse finale. Dans ce cas, la réponse serait 1,412 reste 1.
* Lorsque vous regardez les décimales, vous pouvez échanger le compteur 1s restant contre dix compteurs 0,1 et continuer la division comme décrit ci-dessus. Les étudiants sont familiers avec ce modèle car il peut aider à démystifier la division avec des décimales avec lesquelles les étudiants peuvent lutter. Cela les aide à voir que c’est la continuation d’un processus qu’ils connaissent déjà plutôt que quelque chose de nouveau.
Problèmes de division Année 5
Lors de la division en année 5, les élèves rencontreront des scénarios dans lesquels ils devront arrondir leur réponse pour que la réponse ait un sens dans le contexte. Une question appropriée qui démontre cela serait quelque chose comme la suivante:
Une école planifie une discothèque distanciée sociale où elle prévoit d’offrir 250 ml de jus à chaque élève. Ils peuvent acheter des bouteilles de jus de 2 litres. Ils attendent l’arrivée de 33 étudiants, alors sachez que cela donnera 8,25 litres de jus. Combien de bouteilles de jus devront-ils acheter?
Une réponse courante est que les étudiants diront 4 et quart. Cependant, comme vous ne pouvez pas acheter un quart de bouteille, dans ce cas, la bonne réponse serait que 5 bouteilles de jus seraient nécessaires pour que tous les étudiants puissent participer.
Division: Raisonnement et résolution de problèmes Année 5
Comme indiqué ci-dessus, en année 5, les élèves rencontreront des scénarios au sein de la division où ils devront choisir si une réponse doit être arrondie à la hausse ou à la baisse. Par exemple, lorsqu’une question demande aux élèves de déterminer combien d’autobus sont nécessaires pour un voyage scolaire.
Amener les élèves à créer leurs propres problèmes en utilisant une gamme de contextes fournis peut être une activité vraiment difficile qui amène les élèves à réfléchir mathématiquement au contexte et à la division.
Les élèves peuvent ensuite échanger ces questions qu’ils ont créées avec un partenaire, puis les résoudre et vérifier auprès du créateur de la question originale s’ils ont la bonne réponse.
Année de division 6
Dans le Programme national de mathématiques en Angleterre, pour chaque domaine de mathématiques décrit, il y a à la fois un élément statutaire et un élément non statutaire. L’élément statutaire est le suivant:
- diviser des nombres jusqu’à 4 chiffres par un nombre entier à deux chiffres en utilisant la méthode écrite formelle de division longue, et interpréter les restes comme des restes de nombres entiers, des fractions ou en arrondissant, selon le contexte
- diviser des nombres jusqu’à 4 chiffres par un nombre à deux chiffres en utilisant la méthode écrite formelle de division courte, le cas échéant, interpréter les restes selon le contexte
- effectuer des calculs mentaux, y compris avec des opérations mixtes et de grandes les nombres
- identifient les facteurs communs, les multiples communs et les nombres premiers
- utiliser leur connaissance de l’ordre des opérations pour effectuer des calculs impliquant les quatre opérations
Notes et directives non statutaires:
- Résoudre des problèmes d’addition, de soustraction, de multiplication et de division
- Utiliser l’estimation pour vérifier les réponses aux calculs et déterminer, dans le contexte d’un problème, un degré de précision approprié.
Idées de cours de division Année 6
Sophie Bartlett (@_MissieBee) a créé un excellent blog ici (lien vers le blog de Sophie sur l’enseignement de la division longue) détaillant comment elle enseignerait la division longue pour une classe de 6e année. Comme la division longue est le seul nouvel apprentissage de la division pour la 6e année, c’est un moyen idéal d’introduire la procédure de division longue.
Questions de division 6e année
Un problème typique de mot de division qu’un élève de 6e année rencontrerait serait:
Une école a recueilli 3 146 £ grâce à une vente de pâtisseries. 104 parents ont assisté à l’événement. Si tous les parents ont dépensé une somme d’argent égale, combien chaque parent a-t-il dépensé?
Ici, les étudiants devraient utiliser la méthode de la division longue pour résoudre cette question pour obtenir la réponse £ 30.25.
Division: Raisonnement et Résolution de problèmes 6e année
Avec quelque chose de procédural comme une longue division, une bonne activité de raisonnement consiste à amener les élèves à trouver des erreurs. Ces ressources fournissent une grande banque de ces activités. Comme nous pouvons le voir sur la question ci-dessous, les élèves ont fait tout le travail, mais une erreur négligente dans le comptage des groupes de 59 signifie que l’enfant croyait que 59 x 7 était 472 et non 59 x 8.
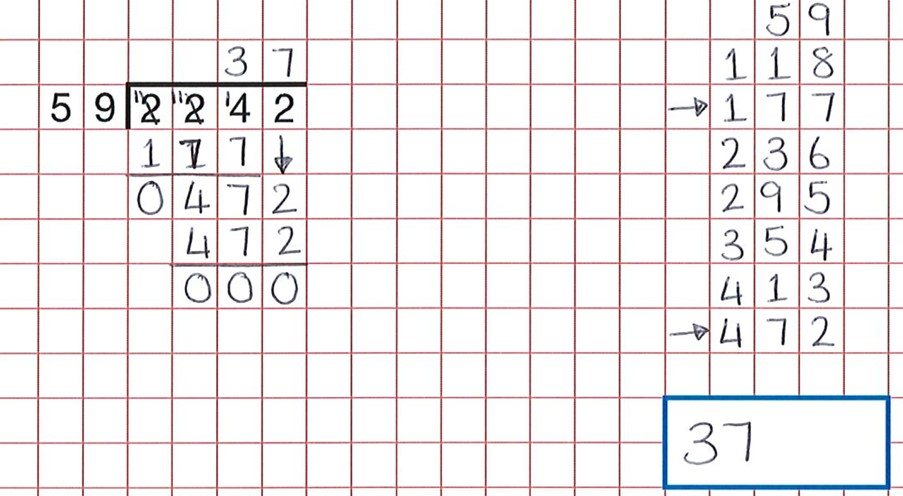
La bonne réponse aurait été 38.
La division est un sujet de mathématiques clé, pas seulement au KS2 mais dans les mathématiques dans leur ensemble. J’espère que cet article vous a donné de bonnes idées pour aider vos élèves à l’aborder avec confiance.
Cours de mathématiques 1 à 1 en ligne approuvés par les écoles et les enseignants
Chaque semaine, les tuteurs spécialisés en mathématiques de Third Space Learning soutiennent des milliers d’enfants du primaire avec des leçons hebdomadaires en ligne 1 à 1 et des interventions en mathématiques. Depuis 2013, nous avons aidé plus de 100 000 enfants à devenir des mathématiciens plus confiants et capables. En savoir plus ou demander un devis personnalisé pour nous parler de vos besoins et de la façon dont nous pouvons vous aider.
L’enseignement primaire est axé sur les besoins de chaque enfant et suit de près le programme national.