Les sommets, les faces et les arêtes apparaissent beaucoup dans la géométrie de l’école primaire lorsque les enfants apprennent les propriétés des formes 3d. Nous expliquons ici ce que chacun d’eux signifie et comment calculer le nombre de sommets, de faces et d’arêtes pour n’importe quelle forme. Nous incluons également le nombre d’arêtes, de faces et de sommets des formes les plus courantes.
Ce vocabulaire est introduit dans le programme national à la 2e année, et les informations suivantes peuvent donc être utilisées avec les élèves tout au long des années d’école primaire. Même les élèves de l’année 1 peuvent commencer à s’intéresser aux propriétés des formes de cette manière si vous voulez leur donner une longueur d’avance!
Que sont les sommets dans les formes?
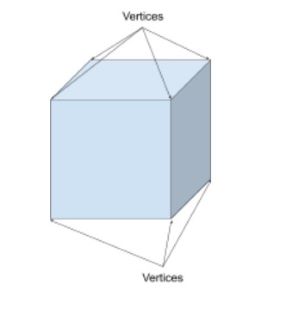
Les sommets dans les formes sont les points où deux segments ou arêtes de ligne ou plus se rencontrent (comme un coin). Le singulier des sommets est sommet. Par exemple, un cube a 8 sommets et un cône a un sommet.
Les sommets sont parfois appelés coins, mais lorsqu’il s’agit de formes 2D et 3D, le mot sommets est préféré.
Un cube a 8 sommets. 7 sont visibles ici et l’un est caché.
Que sont les arêtes?
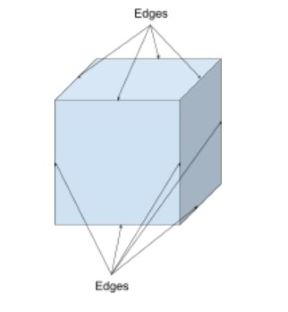
Les arêtes sont les segments de ligne qui joignent un sommet à un autre et sont également l’endroit où les faces de la forme se rencontrent. Ceux-ci peuvent être utilisés pour décrire des formes 2d et 3d.
Bien que de nombreuses formes aient des lignes droites et des bords droits, il existe des formes qui ont des bords incurvés, comme un hémisphère. Un cube aura 12 bords droits comme on le voit ci-dessous; 9 sont visibles et 3 sont cachés.

Feuilles de calcul de récapitulation indépendantes de Formes 3D GRATUITES
Aidez vos élèves de 2 ans (et plus) à réviser les sommets, les faces et les arêtes avec nos feuilles de calcul de récapitulation indépendantes gratuites.
Que sont les visages ?
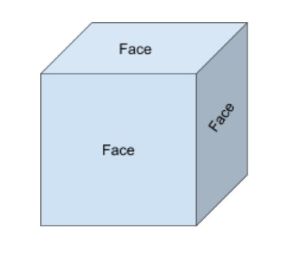
Les faces sont la surface plane d’une forme solide. Par exemple, un cuboïde a 6 faces. Lorsque l’on pense aux formes 2d et 3d, il est important de savoir qu’une forme 2d représente simplement la face d’une forme 3d.
Il est également important de savoir que notre réalité étant construite en 3 dimensions, il est impossible de manipuler physiquement des formes 2d car nous sommes entourés de formes en 3 dimensions. Par conséquent, si dans votre classe il y a un tiroir étiqueté « Formes 2d », cela devrait être supprimé car il enseigne aux enfants une idée fausse. Bien qu’un concept interactif pour la salle de classe, les formes 2d ne peuvent exister que sous forme de dessins en 2 dimensions.
Vous pouvez avoir à la fois des faces plates et des faces courbes, mais je trouve utile de désigner les faces courbes comme des surfaces courbes car cela correspond bien au visuel de la forme.
Il y a trois faces qui sont visibles et trois qui sont cachées sur le cube ci-dessous.
Sommets, faces et arêtes de formes 3d communes
Combien de faces, d’arêtes et de sommets un cuboïde a-t-il?
Un cuboïde a 8 sommets.
Un cuboïde a 12 bords.
Un cuboïde a 6 faces.

Combien de faces, d’arêtes et de sommets un cylindre a-t-il?
Un cylindre a 0 sommet.
Un cylindre a 2 bords.
Un cylindre a 2 faces et 1 surface incurvée.

Combien de faces, d’arêtes et de sommets un hémisphère a-t-il?
Un hémisphère a 0 sommet.
Un hémisphère a 1 bord incurvé.
Un hémisphère a 1 face et 1 surface incurvée.

Combien de faces, d’arêtes et de sommets un cône a-t-il?
Un cône a 1 sommet.
Un cône a 1 bord.
Un hémisphère a 1 face et 1 surface incurvée.

Combien de faces, d’arêtes et de sommets un tétraèdre a-t-il?
Un tétraèdre a 4 sommets.
Un tétraèdre a 6 arêtes.
Un tétraèdre a 4 faces.

Combien de faces, d’arêtes et de sommets une sphère a-t-elle?
Une sphère a 0 sommet.
Un tétraèdre a 0 arêtes.
Un tétraèdre a 1 surface incurvée.

Combien de faces, d’arêtes et de sommets un prisme a-t-il?
Un prisme est un objet solide, une forme géométrique ou un polyèdre dont les faces des deux extrémités ont la même forme. À ce titre, les élèves rencontreront de nombreux types de prismes tout au long de leur scolarité. Les plus courants comprennent les cubes, les cuboïdes, les prismes triangulaires, les prismes pentagonaux et les prismes hexagonaux.
| Forme | Image | Faces | Arêtes | Sommets |
|---|---|---|---|---|
| Prisme Triangulaire | 5 | 9 | 6 | |
| Prisme Pentagonal | 7 | 15 | 10 | |
| Prisme Hexagonal | 8 | 18 | 12 | |
| Cube | 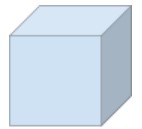 |
6 | 8 | 12 |
| Cuboïde |  |
6 | 8 | 12 |
Quand les enfants apprennent-ils les sommets, les faces et les arêtes à l’école primaire?
Les enfants doivent être formellement initiés au vocabulaire des sommets, des faces et des arêtes en année 2 lorsqu’ils étudient la géométrie. Cependant, les enseignants peuvent faire le choix d’introduire ce vocabulaire plus tôt.
Les élèves de l’année 2 devraient pouvoir ::
- identifier et décrire les propriétés des formes 3D, y compris le nombre d’arêtes, de sommets et de faces
Les directives non statutaires indiquent que:
- Les élèves manipulent et nomment une grande variété de formes 2d et 3d courantes, y compris: des quadrilatères et des polygones, des cuboïdes, des prismes et des cônes, et identifient les propriétés de chaque forme (par exemple, le nombre de côtés, le nombre de faces). Les élèves identifient, comparent et trient les formes en fonction de leurs propriétés et utilisent le vocabulaire avec précision, comme les côtés, les arêtes, les sommets et les faces.
À partir de ce moment, le programme national ne fait plus explicitement référence aux sommets, aux faces et aux arêtes, de sorte que les enseignants des autres groupes d’année devront continuer à utiliser ce vocabulaire lorsqu’ils examineront shape
Comment les sommets, les faces et les arêtes se rapportent-ils à d’autres domaines des mathématiques?
Les étudiants utiliseront les connaissances des sommets, des faces et des arêtes lorsqu’ils examineront des formes 2d ainsi que des formes 3d. Connaître les bords et les identifier sur les formes composées est crucial pour trouver le périmètre et l’aire des formes composées 2d. C’est une base importante pour les années ultérieures lorsqu’il s’agit de différents théorèmes mathématiques, tels que la théorie des graphes et les paraboles.
Comment les sommets, les faces et les arêtes se rapportent-ils à la vie réelle?
Tout objet dans la vie réelle a des sommets, des faces et des arêtes. Par exemple, un cristal est un octaèdre – il a huit faces, douze arêtes et six sommets. Connaître ces propriétés pour différentes formes tridimensionnelles jette les bases de diverses industries telles que l’architecture, le design d’intérieur, l’ingénierie et plus encore.
Sommets, faces et arêtes exemples de questions
1. Expliquez ce qu’est un sommet.
(Réponse: Un sommet est l’endroit où deux lignes se rencontrent)
2. Combien de bords a un prisme triangulaire?
(Réponse: 9)
3. Combien de sommets un cône a-t-il?
(Réponse: 1 sommet)
4. Combien de faces a un cuboïde? Quelles sont les formes 2D de ces visages ?
(Réponse: 6 visages. Ils peuvent avoir 2 faces carrées et 4 faces rectangulaires ou seulement 6 faces rectangulaires.)
5. Pour tous les prismes communs (cubes, cuboïdes, prismes triangulaires, prismes pentagonaux et prismes hexagonaux), additionnez les faces et les sommets et soustrayez les bords. Que remarquez-vous des réponses ?
(Réponse: La réponse est toujours 2. C’est ce qu’on appelle la formule d’Euler (nombre de sommets – nombre d’arêtes + nombre de faces = 2)
Vous vous demandez comment expliquer un autre vocabulaire mathématique clé à vos enfants? Consultez notre dictionnaire de mathématiques primaire, ou essayez-les:
- Qu’est-ce que la maîtrise des mathématiques ?
- Que sont les formes 2d ?
- Que sont les formes 3D ?
Vous pouvez trouver de nombreux plans de cours de géométrie et des feuilles de travail imprimables pour les élèves du primaire sur le troisième espace Learning Maths Hub.
Cours de mathématiques 1 à 1 en ligne approuvés par les écoles et les enseignants
Chaque semaine, les tuteurs spécialisés en mathématiques de Third Space Learning soutiennent des milliers d’enfants du primaire avec des leçons hebdomadaires en ligne 1 à 1 et des interventions en mathématiques. Depuis 2013, nous avons aidé plus de 100 000 enfants à devenir des mathématiciens plus confiants et capables. En savoir plus ou demander un devis personnalisé pour nous parler de vos besoins et de la façon dont nous pouvons vous aider.
Notre programme de cours en ligne pour les mathématiques fournit à chaque enfant son propre tuteur professionnel en mathématiques