In questa guida spiegherò cos’è la formula di errore standard e come usarla per risolvere l’errore standard attraverso l’uso di un esempio.
Qual è l’errore standard?
L’errore standard (SE), a volte indicato come errore standard della media (SEM), è una statistica che corrisponde alla deviazione standard di una distribuzione di campionamento, rispetto al valore medio. Ma che cosa è in realtà che?
Dì che sei interessato all’età media alle persone nel Regno Unito viene diagnosticata la malattia di Alzheimer. Non è possibile determinare questo per tutti nel Regno Unito, quindi i ricercatori prendono una popolazione campione per generalizzare una cifra complessiva. Ad esempio, 10.000 persone britanniche con la malattia possono essere analizzate e saranno utilizzate per generare l’età media della diagnosi. Se lo fai su un campione casuale di 5.000 pazienti, potresti ottenere un’età media di diagnosi di 61,5 anni. Tuttavia, se si esegue l’analisi del campione su un campione casuale separato di altri 10.000 pazienti, è possibile ottenere un’età media di 62,3 anni. Diciamo, ipoteticamente parlando naturalmente, che se si fosse in grado di analizzare tutte le persone nel Regno Unito che hanno il morbo di Alzheimer per ottenere la cifra reale, si può finire con 64,3 anni. Si può notare che le cifre ottenute dalle popolazioni campione (61,5 e 62,3 anni) differiscono dalla cifra reale (64,3 anni). Questa variazione nei valori medi è prevista e man mano che aumenti il numero di persone nella tua popolazione campione otterrai un valore più vicino alla cifra reale. Questo è esattamente ciò che rappresenta l’errore standard. L’errore standard indica questa variazione nei valori medi tra le popolazioni campione.
Per ulteriori letture, ti suggerisco di leggere la breve nota statistica dei professori Douglas Altman e Martin Bland pubblicata sul British Medical Journal. Si tratta di una visione utile in ciò che l’errore standard è e ciò che la differenza con la deviazione standard.
La formula di errore standard
Per calcolare l’errore standard, è necessario disporre di due informazioni: la deviazione standard e il numero di campioni nel set di dati. L’errore standard viene calcolato dividendo la deviazione standard per la radice quadrata del numero di campioni.
Ecco la formula di errore standard annotata completa:
Esempio
Per comprendere meglio la formula di errore standard, potrebbe essere utile passare attraverso un esempio. Diciamo che abbiamo una popolazione di 80 persone e siamo interessati alla loro altezza. Misuriamo la loro altezza e calcoliamo la deviazione standard come 30,6 cm. Ora dobbiamo inserire questi valori nella nostra equazione:
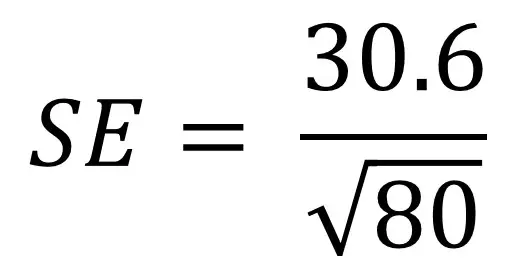Se non sei a tuo agio nell’inserire equazioni nelle calcolatrici, puoi suddividere la formula in blocchi gestibili. Ecco i passi che puoi fare.
- In primo luogo, calcolare la radice quadrata del numero di campioni (n). In questo caso, n è 80. La radice quadrata di 80 è 8.94.
- Quindi, dividere la deviazione standard (30.6) per la radice quadrata di 80 (8.94). Facendo questo dà un valore di 3.42.
- Pertanto, l’errore standard nella nostra popolazione per altezza è di 3,42 cm.