La divisione nella fase chiave 2 costituisce l’ultima parte delle “Quattro operazioni” – i quattro concetti matematici fondamentali che gli alunni dovrebbero conoscere. Questo blog ti aiuterà a garantire che tutti i tuoi alunni, dall’anno 3 all’anno 6, possano avvicinarsi alla divisione con la sicurezza di cui hanno bisogno per avere successo.
La divisione in matematica KS2 si basa su ciò che è stato appreso in KS1. Entro la fine di Y2 gli studenti presso lo standard previsto saranno in grado di ‘richiamare e utilizzare fatti di moltiplicazione e divisione per le tabelle di moltiplicazione 2, 5 e 10, compreso il riconoscimento di numeri pari e dispari.’
Per gli insegnanti dell’anno 3, è sempre una buona idea assicurarsi che gli studenti li conoscano molto bene. Con ciò, non intendo semplicemente che possano pappagallare i fatti di divisione, ma capiscono veramente come rappresentare questi fatti sia con rappresentazioni concrete, spiegazioni verbali che attraverso altri metodi pittorici.
Gli studenti che non sono in grado di farlo, ma sono in grado di dirti verbalmente i fatti della divisione, hanno una comprensione molto superficiale della divisione e per loro di progredire in attività di problem solving più difficili, approfondire la loro comprensione concettuale della divisione è un must all’anno 3.
Il Curriculum nazionale colloca la divisione all’interno della stessa sezione della moltiplicazione per gli anni 3-5 e la colloca all’interno di una sezione chiamata “Quattro operazioni” nell’anno 6. Le parti tratte dal Curriculum nazionale si riferiscono solo a quelle che menzionano specificamente la divisione. Gli altri elementi di tali sezioni possono essere trovati nel blog sulla moltiplicazione o addizione e sottrazione, se del caso.
Che cos’è la divisione?
La divisione è una delle quattro operazioni – i quattro concetti matematici fondamentali che gli alunni dovrebbero conoscere – insieme all’addizione e alla sottrazione e alla moltiplicazione.
Dove la moltiplicazione combina un numero più volte, la divisione è l’opposto: calcolare quante volte un numero è contenuto in un altro. Ad esempio, dividendo 10 per 2 si chiede quante volte 2 è contenuto all’interno di 10.

dagli interventi di matematica online di Third Space Learning.
Divisione didattica KS2-La teoria
La divisione è l’inverso della moltiplicazione. Come con il blog moltiplicazione, l’insegnamento della divisione contiene tre strutture sottostanti, che, quando accoppiato con fatti divisione e comprensione concettuale darà agli studenti la migliore opportunità di avere successo quando risolvere i problemi legati alla divisione.
Le tre strutture sono condivisione, raggruppamento e ridimensionamento. Mentre non c’è abbastanza tempo per esplorare questi in profondità, quello che segue sarà solo una breve introduzione a loro.
La condivisione e il raggruppamento sono l’inverso della moltiplicazione come aggiunta ripetuta. La condivisione è un concetto strutturale che viene introdotto in KS1 e precedenti in cui, come suggerisce il nome, un importo è condiviso in gruppi uguali.
Ad esempio, 12 mele sono condivise tra 3 studenti. Quante mele ottiene ogni studente? Qui sappiamo l’intero importo (12 mele) e soprattutto, sappiamo come l’importo che stiamo per condividere in (3). A seconda di dove gli studenti sono nel loro viaggio matematico, possono ripetutamente sottrarre da un certo numero (1, 2, 3 o 4) dall’importo in tre pile che rappresentano i tre studenti.
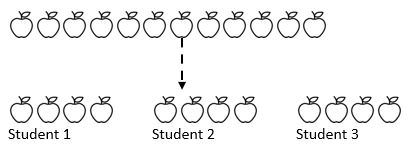
Come possiamo vedere da quanto sopra, l’intero importo è stato condiviso in tre gruppi uguali.
Il raggruppamento è simile alla condivisione, ma ciò che sappiamo è leggermente diverso rispetto alla condivisione. Nella struttura di condivisione, conosciamo la quantità di gruppi che la condivisione avrà luogo. Nella struttura di raggruppamento, conosciamo la quantità in ogni gruppo ma non il numero di gruppi effettivi che ci sono.
Ad esempio, 12 mele sono condivise in gruppi di 4. Quanti gruppi ci saranno? Mentre questa domanda è molto simile a quella sopra, ora assume la struttura di raggruppamento in quanto sappiamo quanti andranno in ciascun gruppo ma non sappiamo più quanti gruppi ci saranno ora.
Poiché sappiamo che ci sono 4 in ogni gruppo, possiamo raggruppare 4 mele fino a quando non abbiamo coperto tutti i 12 per vedere che ci sono 3 gruppi.
La struttura finale della divisione è in scala. Mentre nella moltiplicazione stavamo scalando un valore, la struttura della divisione si ridimensiona. Ad esempio, Shannen ha 6 penne e Jen ha 3 volte meno. Quante penne ha Jen?
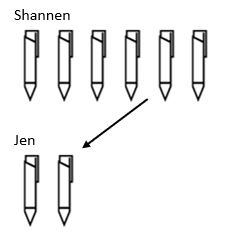
Qui possiamo vedere che per trovare la quantità totale di penne che Jen ha, abbiamo dovuto prendere la quantità che Shannen aveva e diminuirlo di un fattore di scala di 3 in modo che Jen finisce con 2 penne.
Per esperienza, questa è la struttura di divisione più difficile da comprendere e comprendere per gli studenti ed è una struttura che deve essere rivisitata in combinazione con il ridimensionamento come moltiplicazione in quanto questa è un’abilità cruciale quando si convertono misure e valute da una quantità maggiore a una quantità minore. Ad esempio Chilometri a miglia.
Divisione Anno 3
Nel Curriculum nazionale per la matematica in Inghilterra, per ogni area di matematica delineata, c’è sia un elemento statutario che un elemento non statutario. L’elemento statutario è il seguente:
- Richiamare ed utilizzare la moltiplicazione e la divisione fatti per il 3, 4 e 8 tavole di moltiplicazione
- Scrittura e calcolo matematico istruzioni per la moltiplicazione e la divisione utilizzando le tabelle di moltiplicazione che sanno, anche per i numeri di due cifre tempi di numeri di una cifra, utilizzando mentale e procedendo alla formale scritta di metodi
- Risolvere i problemi, compreso il numero mancante, che coinvolgono la moltiplicazione e la divisione, compreso numero intero positivo problemi di scaling e la corrispondenza problemi di n oggetti sono collegati a m oggetti.
Non legge le note e di orientamento:
- gli Studenti a sviluppare efficienti metodi mentali, per esempio, l’utilizzo di commutativity e associatività (per esempio, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) e la moltiplicazione e la divisione dei fatti (ad esempio, utilizzando 3 × 2 = 6, 6 ÷ 3 = 2 e 2 = 6 ÷ 3) per ricavare fatti correlati (per esempio, 30 × 2 = 60, 60 ÷ 3 = 20 e 20 = 60 ÷ 3).
- Gli alunni sviluppano metodi scritti affidabili per la moltiplicazione e la divisione, iniziando con calcoli di numeri a due cifre per numeri a una cifra e procedendo ai metodi scritti formali di moltiplicazione e divisione brevi.
- Gli alunni risolvono semplici problemi in contesti, decidendo quale delle quattro operazioni usare e perché. Questi includono contesti di misurazione e ridimensionamento, (ad esempio, quattro volte più alti, otto volte più lunghi ecc.) e problemi di corrispondenza in cui m oggetti sono collegati a n oggetti (ad esempio, 3 cappelli e 4 cappotti, quanti abiti diversi?; 12 dolci condivisi equamente tra 4 bambini; 4 torte condivise equamente tra 8 bambini).
Attività di divisione Anno 3
Questo non coprirà una lezione di per sé, ma fornirà una guida su come la divisione può essere insegnata con una certa comprensione concettuale in questa fase. Un pre-requisito per questo sarebbe l’insegnamento dei fatti di moltiplicazione correlati prima di insegnare qualsiasi divisione correlata.
Quando si pensa alle strutture, è meglio in questa parte del viaggio di apprendimento degli studenti attenersi al raggruppamento e alla condivisione. Per i seguenti esempi, vedremo lo sviluppo di studenti comprensione della divisione per 4. Seguirà l’approccio Concreto-Pittorico-Astratto.
È spesso la comprensione del numero degli studenti che può limitare i loro progressi nella divisione. Soprattutto quando si tratta di raggruppare e condividere quando ne tolgono uno solo continuamente dal tutto.
Fin dall’inizio della divisione di insegnamento, gli insegnanti dovrebbero appoggiarsi su ciò che gli studenti sanno già sui numeri pari e altri fatti numerici per far progredire gli studenti sul conteggio in qualsiasi numero possa essere appropriato.
I contatori possono essere utilizzati per dimostrare fatti di divisione correlati in quanto gli studenti avranno usato le tesi quando costruiscono la loro comprensione concettuale della moltiplicazione. Domande come, ‘ Quanti gruppi di 4 ci sono? e ‘ quanti ce ne sono in ogni gruppo?”dovrebbe essere chiesto e le risposte dovrebbero riguardare il modo in cui questo dimostra la divisione.
Insegnante: Quanti contatori ci sono?
Bambino: Quattro
Insegnante: Buono. Questo è un gruppo di quattro. Quanti gruppi di quattro ci sono?
Bambino: Uno
Insegnante: Eccellente. Abbiamo quattro contatori in un gruppo. Abbiamo raggruppato quattro contatori in un unico gruppo. Cosa abbiamo fatto?
Bambino: raggruppato quattro contatori in un unico gruppo.
Insegnante: Brillante. Quando raggruppiamo quattro contatori in un gruppo abbiamo fatto il calcolo matematico di quattro divisi per uno. Che calcolo abbiamo fatto?
Bambino: quattro divisi per uno.
Insegnante: E quando risolviamo quattro divisi per uno la risposta è quattro perché abbiamo creato un gruppo che ha quattro elementi in esso. Quattro diviso uno fa quattro. Che cosa è quattro diviso per uno?
Bambino: Quattro diviso uno fa quattro.
Insegnante: Eccellente
Puoi vedere come sarebbe ripetuto per quanto segue:
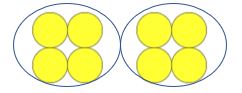
Insegnante: Quanti contatori ci sono?
Bambino: Otto
Insegnante: Buono, questo è un gruppo di quattro. Quanti gruppi di quattro ci sono?
Bambino: Due
Insegnante: Eccellente. Abbiamo quattro contatori in un gruppo. Abbiamo raggruppato quattro contatori in due gruppi. Cosa abbiamo fatto?
Bambino: raggruppato quattro contatori in due gruppi.
Insegnante: Brillante. Quando raggruppiamo quattro contatori in due gruppi abbiamo fatto il calcolo matematico di otto diviso per due. Che calcolo abbiamo fatto?
Bambino: Otto diviso due.
Insegnante: E quando risolviamo otto divisi per due la risposta è quattro perché abbiamo fatto due gruppi che hanno quattro elementi in esso. Otto diviso due fa quattro. Che cosa è otto diviso per due?
Bambino: Otto diviso due fa quattro.
Insegnante: Eccellente
Quando gli studenti stanno cominciando ad avere fiducia in questo, possiamo passare ad altri modelli come aste Cuisenaire.

Qui l’intero importo è rappresentato nel treno superiore e l’asta viola (che in questo caso rappresenta 4 e se avete letto altri blog in questa serie si spera si sa quanto di un avvocato sono per il loro uso in classe e così gli studenti saranno consapevoli del suo valore da allora) viene utilizzato per mostrare quanti gruppi di 4 possono andare nella quantità totale.
Gli studenti possono quindi passare a disegnare scenari letti dall’insegnante. Biru. Ci sono 24 pulsanti e devono essere raggruppati in 4. Quanti gruppi ci sono? Gli studenti potrebbero disegnare quei pulsanti e raggrupparli in 4 ecc.
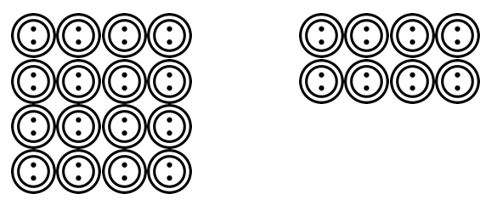
Una volta che gli studenti si sono abituati a essere in grado di visualizzare questi scenari di raggruppamento o condivisione di divisioni in una serie di contesti, possono passare a rappresentazioni più astratte usando simboli matematici.

3 Fogli di lavoro a divisione lunga per anni 3-6
Prepara i tuoi alunni per la divisione lunga in KS2 con questi fogli di lavoro a divisione lunga.
Divisione Problemi di parole Anno 3
Problemi di parole nell’anno 3 useranno comunemente la struttura di raggruppamento o condivisione.
Ci sono 40 torte e 10 studenti. Quante torte otterrebbe ogni studente?
Poiché sappiamo quanti gruppi ci sono (10), dobbiamo calcolare l’importo per gruppo, quindi questa è una struttura di condivisione. Gli studenti dovrebbero usare la loro conoscenza della tabella dei tempi 4 per risolvere questo problema e ottenere la risposta 4.
Divisione: Ragionamento e Problem Solving Anno 3
Per il ragionamento e il problem solving, una buona attività che trovo è quella di abbinare un problema di parole a un calcolo. Ad esempio:
Abbina i problemi di parola che vengono risolti conoscendo 20 diviso per 4.
- Ci sono 20 matite e stanno per essere collocati in confezioni da 5. Quanti in ogni confezione?
- C’erano 20 matite e poi uno studente ne porta altre 4. Quante matite ci sono adesso?
- Ci sono 20 matite e stanno per essere collocati in confezioni da 4. Quanti in ogni confezione?
- C’erano 20 matite e poi 4 scompaiono. Quante matite ci sono adesso?
Convincere gli studenti a scrivere le loro spiegazioni per ogni domanda è utile in quanto consente di vedere il loro pensiero. Le domande sono state selezionate con attenzione in modo che i numeri in ogni domanda si riferiscono ai numeri sulla domanda così gli studenti si affidano alle loro abilità matematiche per dedurre la risposta corretta.
Divisione Anno 4
Nel Curriculum nazionale per la matematica in Inghilterra, per ogni area di matematica delineata, c’è sia un elemento statutario che un elemento non statutario. L’elemento statutario è il seguente:
- Richiamare moltiplicazione e divisione fatti per tabelline fino a 12 × 12
- Utilizzare il valore di luogo, fatti noti e derivati per moltiplicare e dividere mentalmente, tra cui: moltiplicando per 0 e 1; dividendo per 1; moltiplicando insieme tre numeri
Note e linee guida non statutarie:
- Gli alunni continuano a praticare il richiamo e l’uso di tabelline e fatti di divisione correlati per facilitare la fluidità.
- Gli alunni praticano metodi mentali ed estendono questo a numeri a tre cifre per ricavare fatti, (ad esempio 600 ÷ 3 = 200 può essere derivato da 2 x 3 = 6).
- Gli alunni si esercitano a diventare fluenti nel metodo scritto formale di moltiplicazione breve e divisione breve con risposte esatte
- Gli alunni risolvono problemi in due fasi in contesti, scegliendo l’operazione appropriata, lavorando con numeri sempre più difficili. Questo dovrebbe includere domande di corrispondenza come il numero di scelte di un pasto su un menu, o tre torte condivise equamente tra 10 bambini.
Idee per le lezioni di divisione Anno 4
Per questa lezione, guarderò come puoi iniziare a insegnare la divisione breve usando i manipolativi accanto ad essa.
Diciamo che stiamo per insegnare agli studenti breve divisione per la domanda 168 diviso per 12.
Normalmente scriveremmo questo in quella che viene comunemente chiamata fermata dell’autobus. Ma ciò che è interessante è che diversi posti nel mondo lo scrivono in modo diverso.
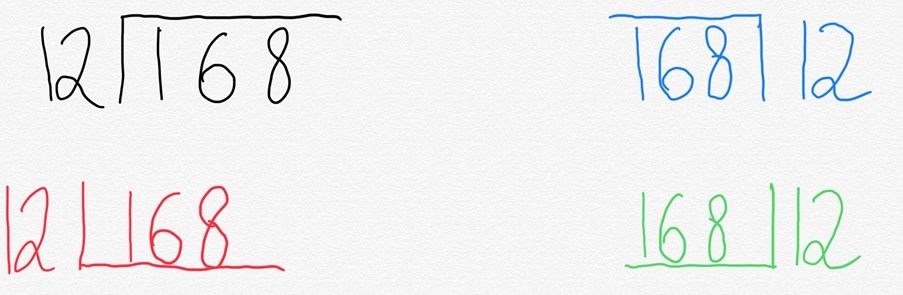
La ragione di questo è abbastanza semplice. Ciò che la “fermata dell’autobus” rappresenta effettivamente è un modo abbreviato per rappresentare un rettangolo.
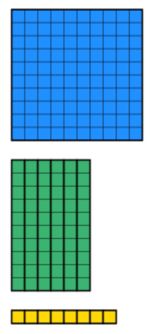
Quando insegniamo la divisione breve formale, ciò che stiamo effettivamente dicendo è che devi immaginare un rettangolo in cui la larghezza è 12. L’area totale del rettangolo è 168 e stiamo tentando di trovare la lunghezza mancante nella parte superiore. Quindi, come mostriamo questo usando manipolativi? I blocchi Dienes sono uno strumento utile per questo.
Sappiamo che l’importo totale è 168. Quindi abbiamo bisogno di raccogliere 168 di dienes usando la più piccola quantità di blocchi possibili. Questo è mostrato di seguito.
Guardando indietro alla domanda, sappiamo che la larghezza è 12. Ciò significa che ora dobbiamo manipolare i blocchi in modo da ottenere una larghezza di 12. Si noti che il rettangolo deve essere solido e non può avere parti mancanti. Ad esempio, il sotto non sarebbe consentito nonostante ci siano 12 unità che scendono dalla larghezza.
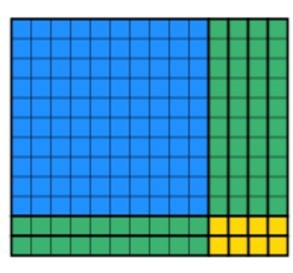
Invece, gli studenti possono ruotare due blocchi di 10s per ottenere quanto segue. Si noti come ci sia 12 in ogni colonna ed è un oggetto solido.
La parte finale che gli studenti devono fare è utilizzare i blocchi rimanenti per creare un rettangolo venduto mantenendo la larghezza 12. Questo potrebbe richiedere del tempo, ma con la pratica, gli studenti diventano più veloci. Dopo un po ‘ di tempo, gli studenti produrranno questo:
Possiamo vedere che tutti i 168 blocchi sono stati esauriti e che la larghezza è ancora 12. Per trovare la risposta, gli studenti sono tenuti a contare la lunghezza, che in questo caso è 14. Ho sovrapposto entrambi i metodi qui sotto in modo da poter vedere come si completano a vicenda qui sotto.
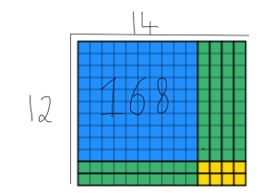
Questa è una strategia utile per insegnare agli studenti nell’anno 4 in quanto vi sono enormi ripercussioni in altre aree del curriculum che sono già illuminate per gli studenti.
Anche se potrebbero non riconoscerlo ancora, insegnando una divisione breve come questa sono già stati introdotti al perimetro e all’area – pensa a quanto tempo di insegnamento può essere salvato quando questa connessione è fatta. Non solo, ma in secondario, questo approccio trasferisce al pensiero algebrico.
Problemi di parole di divisione Anno 4
Gli studenti dovrebbero attingere alla loro conoscenza del valore del luogo per risolvere problemi basati sulla divisione e quindi sarebbe un problema di parole appropriato.
Un frutteto coltivava 4.800 mele in una stagione. Sono messi in confezioni da 4 prima di andare al mercato. Quanti pacchetti ci sono?
Qui gli studenti dovrebbero usare il fatto che 4 x 12 = 48 e come 4.800 è cento volte più di 48, 12 deve anche moltiplicato per 100 per ottenere 1.200
Divisione: Ragionamento e Problem Solving Anno 4
È sempre, a volte o mai vero che la somma di tre numeri pari è divisibile per 4?
Questa domanda offre agli studenti ampie opportunità di sperimentare entro i parametri della domanda. Gli studenti che hanno bisogno di più sostegno possono guardare cantare cifre anche i numeri e gli studenti potrebbero andare fino a quello che si sentono a proprio agio con.
Con domande aperte come questa, è bene fornire un requisito minimo per quanti tentativi gli studenti dovrebbero fare altrimenti spesso sceglieranno di fare il minimo indispensabile.
La risposta a questa domanda è a volte.
Un rapido “trucco” per sapere se un numero è divisibile è guardare le ultime 2 cifre del numero e vedere se quelle sono divisibili per 4. Ad esempio, se un bambino ha trovato la somma di 34, 36 e 38 e ha ottenuto 108, come insegnante so che questo numero è divisibile per 4 poiché le ultime due cifre (08) fanno 8 e sono divisibili per 4. Se un bambino ha scelto 34, 36 e 48 per ottenere 118, so che questo non è divisibile per 4 poiché 18 – le ultime due cifre di 118 – non sono divisibili per 4.
Divisione Anno 5
Nel Curriculum nazionale per la matematica in Inghilterra, per ogni area di matematica delineata, c’è sia un elemento statutario che un elemento non statutario. L’elemento statutario è il seguente:
- Moltiplicare e dividere i numeri mentalmente disegno su fatti noti
- Dividere i numeri di 4 cifre da un numero di cifre utilizzando la scritta formale metodo di breve divisione e interpretare i residui in modo appropriato per il contesto
- Moltiplicare e dividere numeri interi e quelli che coinvolgono i decimali per 10, 100 e 1000
- Risolvere i problemi che coinvolgono la moltiplicazione e la divisione tra usando la loro conoscenza dei fattori e multipli, i quadrati e i cubi
- Risolvere i problemi che coinvolgono l’aggiunta, la sottrazione, la moltiplicazione e la divisione, e una combinazione di questi, compresa la comprensione del significato del segno di uguale
- Risolvono problemi che coinvolgono la moltiplicazione e la divisione, incluso il ridimensionamento per frazioni semplici e problemi che coinvolgono tassi semplici.
Note e orientamenti non statutari:
- Gli alunni interpretano le risposte non intere alla divisione esprimendo i risultati in modi diversi a seconda del contesto, anche con resti, come frazioni, come decimali o arrotondando (ad esempio, 98 ÷ 4 = = 24 r 2 = 24 = 24.5 ≈ 25).
- Gli alunni usano la moltiplicazione e la divisione come inverse per sostenere l’introduzione del rapporto nell’anno 6, ad esempio moltiplicando e dividendo per potenze di 10 nei disegni in scala o moltiplicando e dividendo per potenze di 1.000 nella conversione tra unità come chilometri e metri.
Attività della divisione Anno 5
La divisione nell’anno 5 progredisce attraverso l’uso dei resti nelle risposte. Per questa lezione, guarderò un altro uso manipolativi che gli insegnanti possono utilizzare per insegnare divisione 4-by-1-digit.
Se la domanda era 5,642 diviso per 4, potremmo rappresentare questo usando un grafico del valore posto e contatori del valore posto come possiamo vedere di seguito.
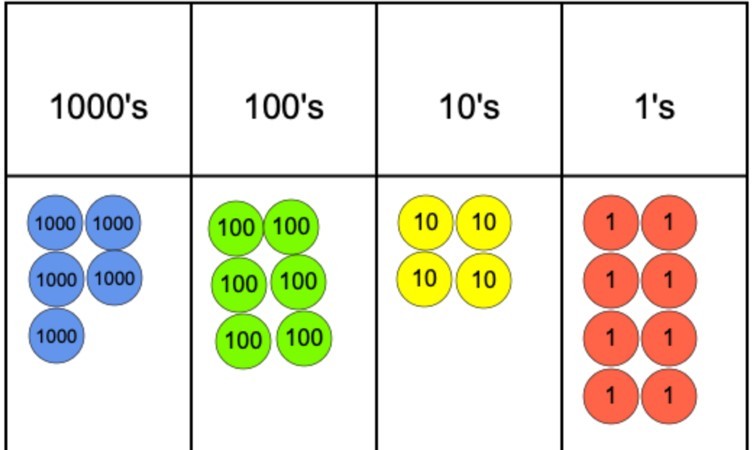
Il prossimo passo sarebbe iniziare a raggruppare i contatori in 4 poiché questo è il nostro divisore. Tuttavia, come si può vedere, arriviamo rapidamente a un problema nella colonna 1000 in quanto siamo in grado di raggruppare 4 dei contatori, ma poi non possiamo raggruppare il contatore rimanente in un gruppo di 4.
Per combattere questo problema, il contatore 1000 che non è stato raggruppato può essere scambiato con dieci contatori 100. Questi possono quindi essere raggruppati in gruppi di 4 e questo può accadere senza che ci siano contatori 100 rimasti. Da lì, è un semplice caso di passare poi agli anni ‘ 10 e infine a quelli.
Poiché ci sono nove contatori 1s, possiamo raggrupparne 8 in 2 gruppi e 4 e affermare che ce n’è uno rimasto*. Per trovare la risposta, tutto ciò che è necessario è contare il numero di gruppi realizzati in ogni valore posto e utilizzare questi per scrivere le cifre per creare la risposta finale. In questo caso, la risposta sarebbe 1.412 resto 1.
*Quando si guardano i decimali, è possibile scambiare il contatore 1s rimanente per dieci contatori 0.1 e continuare la divisione come descritto sopra. Gli studenti che hanno familiarità con questo modello è utile in quanto può aiutare a demistificare la divisione con decimali con cui gli studenti possono lottare. Questo li aiuta a vedere che si tratta di una continuazione di un processo che hanno già familiarità con piuttosto che qualcosa di nuovo.
Problemi di divisione Anno 5
Quando si divide nell’Anno 5, gli studenti si imbatteranno in scenari in cui dovranno arrotondare la loro risposta in modo che la risposta abbia senso nel contesto. Una domanda appropriata che lo dimostra sarebbe qualcosa di simile alla seguente:
Una scuola sta pianificando una discoteca a distanza sociale in cui prevede di offrire 250ml di succo a ogni studente. Possono comprare bottiglie da 2 litri di succo. Si aspettano 33 studenti per arrivare in modo da sapere che darà fuori 8,25 litri di succo. Quante bottiglie di succo avranno bisogno di comprare?
Una risposta comune è che gli studenti diranno 4 e un quarto. Tuttavia, poiché non è possibile acquistare un quarto di bottiglia, in questo caso la risposta corretta sarebbe di 5 bottiglie di succo per garantire che tutti gli studenti potessero partecipare.
Divisione: ragionamento e problem Solving Anno 5
Come notato sopra, nell’Anno 5, gli studenti incontreranno scenari all’interno della divisione in cui saranno tenuti a scegliere se una risposta deve essere arrotondata per eccesso o per difetto. Ad esempio, quando una domanda chiede agli studenti di capire quanti autobus sono necessari per una scuola un viaggio.
Far sì che gli studenti creino i propri problemi utilizzando una serie di contesti forniti può essere un’attività davvero impegnativa che induce gli studenti a pensare matematicamente al contesto e alla divisione.
Gli studenti possono quindi scambiare queste domande che hanno creato con un partner e quindi risolverle e verificare con il creatore della domanda originale se hanno la risposta corretta.
Divisione Anno 6
Nel Curriculum nazionale per la matematica in Inghilterra, per ogni area di matematica delineata, c’è sia un elemento statutario che un elemento non statutario. L’elemento statutario è il seguente:
- dividere i numeri di 4 cifre da un a due cifre numero intero mediante la formale scritta metodo di divisione lunga, e interpretare i residui come numero intero restanti, frazioni, o da arrotondamento, come appropriato per il contesto
- dividere i numeri di 4 cifre da un numero di due cifre utilizzando la scritta formale metodo di breve divisione appropriati, interpretare i residui secondo il contesto
- eseguire calcoli mentali, anche con misto operazioni e dei grandi numeri
- identificare i fattori comuni, comuni multipli e i numeri primi
- utilizzare la loro conoscenza dell’ordine delle operazioni per eseguire calcoli che coinvolgono le quattro operazioni
Note e orientamenti non statutari:
- Risolvere problemi che coinvolgono addizione, sottrazione, moltiplicazione e divisione
- Utilizzare la stima per verificare le risposte ai calcoli e determinare, nel contesto di un problema, un adeguato grado di precisione.
Idee di lezione di divisione Anno 6
Sophie Bartlett (@_MissieBee) ha creato un eccellente blog qui (link al blog di Sophie sull’insegnamento della divisione lunga) in dettaglio come avrebbe insegnato la divisione lunga per una classe di anno 6. Poiché la divisione lunga è l’unico nuovo apprendimento sulla divisione per l’anno 6, questo è un modo ideale per introdurre la procedura di divisione lunga.
Domande di divisione Anno 6
Un tipico problema di parola di divisione che uno studente dell’anno 6 avrebbe incontrato sarebbe:
Una scuola ha raccolto £3.146 da una vendita di torte. 104 genitori hanno partecipato all’evento. Se tutti i genitori hanno speso una quantità uguale di denaro, quanto ha speso ogni genitore?
Qui, gli studenti dovrebbero utilizzare il metodo di divisione lunga per risolvere questa domanda per ottenere la risposta £30.25.
Divisione: ragionamento e Problem Solving Anno 6
Con qualcosa di procedurale come la divisione lunga, una buona attività di ragionamento è quella di convincere gli studenti a trovare errori. Queste risorse forniscono una grande banca di tali attività. Come possiamo vedere dalla domanda qui sotto gli studenti ha fatto tutto il duro lavoro, ma un errore incurante nel contare i gruppi di 59 significa che il bambino credeva 59 x 7 era 472 e non 59 x 8.
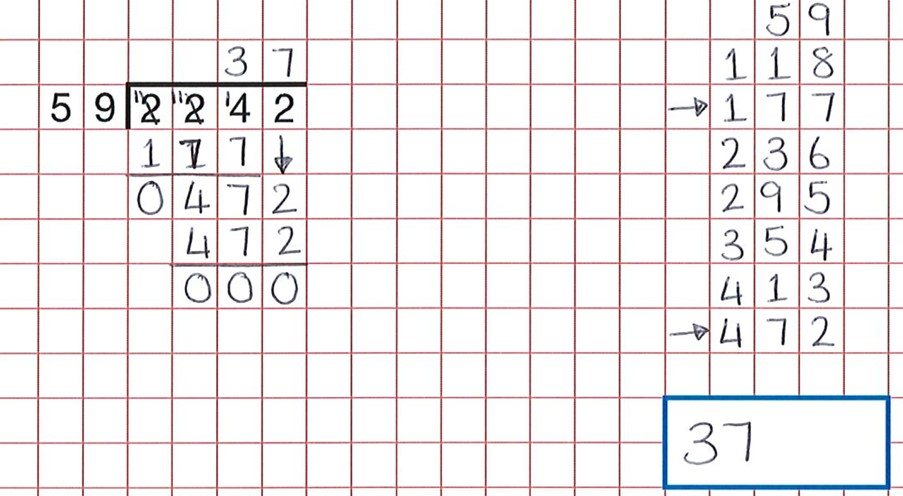
La risposta corretta sarebbe stata 38.
La divisione è un argomento matematico chiave, non solo in KS2 ma in matematica nel suo complesso. Speriamo che questo post ti abbia dato alcune buone idee per aiutare i tuoi alunni ad affrontarlo con sicurezza.
Lezioni online di matematica 1-to-1 affidate a scuole e insegnanti
Ogni settimana i tutor specializzati in matematica di Third Space Learning supportano migliaia di bambini della scuola primaria con lezioni settimanali online 1-to-1 e interventi di matematica. Dal 2013 abbiamo aiutato oltre 100.000 bambini a diventare matematici più sicuri e capaci. Scopri di più o richiedi un preventivo personalizzato per parlarci delle tue esigenze e di come possiamo aiutarti.
Lezioni di scuola primaria mirate alle esigenze di ogni bambino e seguendo da vicino il Curriculum nazionale.