キーステージ2の部門は、”四つの操作”の最後の部分を形成します–四つのコア数学的概念は、生徒が知っておくべきです。 このブログは、3年生から6年生までのすべての生徒が、成功するために必要な自信を持って部門に近づくことができるようにするのに役立ちます。
Ks2数学の除算は、KS1で学んだことに基づいています。 期待される標準のY2学生の終わりまでに、奇数と偶数を認識することを含む、2、5、10の乗算表の乗算と除算の事実を思い出して使用することがで’
3年目の教師にとっては、生徒がこれらをよく知っていることを確認することは常に良い考えです。 それによって、私は単に彼らがあなたに分裂の事実をオウムすることができることを意味するのではなく、具体的な表現、口頭の説明、および他の絵
これができないが、部門の事実を口頭で伝えることができ、部門についての非常に浅い理解を持っており、より困難な問題解決活動に進むためには、3年目に部門の概念的な理解を深めることが必須である。
国のカリキュラムは、3-5年の乗算と同じセクション内に分割を配置し、6年目には”四つの操作”と呼ばれるセクション内に配置します。 国のカリキュラムから取られた部分は、特に部門に言及したものにのみ関連しています。 これらのセクションの他の要素は、必要に応じて乗算または加算と減算に関するブログで見つけることができます。
分割とは何ですか?
除算は、加算と減算、乗算と並んで、生徒が知っておくべき四つのコア数学的概念である四つの演算の一つです。
乗算が1つの数を複数回組み合わせることである場合、除算は反対です:1つの数が別の数に含まれている回数を計算します。 例えば、10を2で割ることは、2が10の中に何回含まれているかを尋ねることです。

に示されているように、互いに逆です。
教示部門KS2-理論
除算は乗算の逆数です。 乗算ブログと同様に、部門の教えは、部門の事実と概念的な理解と相まって、学生に部門に関連する問題を解決する際に成功するための最良の機会を与
三つの構造は、共有、グループ化、スケーリングです。 これらを深く探求するのに十分な時間はありませんが、以下はそれらの簡単な紹介に過ぎません。
共有とグループ化は、繰り返し加算としての乗算の逆数です。 共有は、名前が示すように、金額が等しいグループに共有されるKS1以前に導入された構造的概念です。
例えば、12個のリンゴは3人の学生の間で共有されています。 各学生はどのように多くのリンゴを得るのですか? ここでは、全体の量(12リンゴ)を知っているし、重要なことに、我々はどのように我々は(3)に共有しようとしている量を知っています。 学生が彼らの数学的な旅にある場所に応じて、彼らは繰り返し三人の学生を表す三つの杭に量からいくつかの数(1、2、3または4)で減算することがで
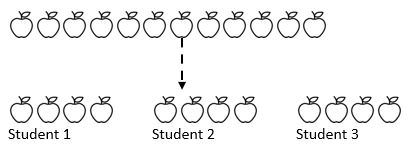
上記からわかるように、全体の金額は3つの等しいグループに共有されています。
グループ化は共有に似ていますが、私たちが知っていることは共有と比較してわずかに異なります。 共有構造では、共有が行われるグループの量を知っています。 グループ化構造では、各グループの量はわかりますが、実際のグループの数はわかりません。
例えば、12個のリンゴは4つのグループで共有されています。 どのように多くのグループがありますか? この質問は上記の質問と非常によく似ていますが、各グループにいくつ入るかはわかっていますが、現在はいくつのグループがあるかはわかりません。
各グループに4つあることがわかっているので、12つすべてをカバーするまで4つのリンゴをグループ化して、3つのグループがあることを確認できます。
分割の最終的な構造はスケーリングです。 乗算では値をスケールアップしていましたが、除算構造はスケールダウンします。 例えば、Shannenには6本のペンがあり、Jenには3倍のペンがあります。 ジェンは何本のペンを持っていますか?
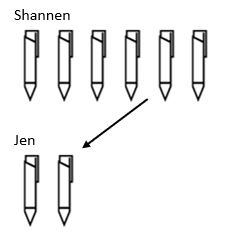
ここでは、Jenが持っているペンの総量を見つけるために、Shannenが持っていた量を取り、Jenが2本のペンで終わるように3のスケール係数で減少させなければ
経験から、これは学生が把握し、理解するのが最も難しい部門構造であり、これは測定値や通貨をより大きな量からより小さな量に変換する際に重要なスキルであるため、乗算としてのスケーリングと併せて再検討する必要があるものである。 例えばマイルへのキロメートル。
Division Year3
イギリスの数学のための国家カリキュラムでは、概説されている数学の各分野には、法定要素と非法定要素の両方があります。 法定要素は次のとおりです:
- 3、4、8の乗算表の乗算と除算の事実を思い出して使用する
- 彼らが知っている乗算表を使用して、二桁の数字に一桁の数字を含め、精神的かつ正式な書かれた方法に進む
- 正の整数スケーリング問題やn個のオブジェクトがm個のオブジェクトに接続されている対応問題を含む、欠落している数の問題を解決する。
法定外の注意事項とガイダンス:
- 生徒は、例えば、可換性と結合性を使用して、効率的な精神的方法を開発する(例えば, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) そして、乗算と除算の事実(例えば、を使用して3 × 2 = 6, 6 ÷ 3 = 2 そして2=6÷3)関連する事実を導出するために(例えば, 30 × 2 = 60, 60 ÷ 3 = 20 および20=60÷3)。
- 生徒は、二桁の数字を一桁の数字で計算することから始まり、短い乗算と除算の正式な書かれた方法に進んで、乗算と除算のための信頼性の高い書
- 生徒は文脈における単純な問題を解決し、四つの操作のうちどれを使用するのか、そしてなぜ使用するのかを決定する。 これには、コンテキストの測定とスケーリングが含まれます(たとえば、高さの四倍、長さの八倍など)。 m個のオブジェクトがn個のオブジェクトに接続されている対応問題(例えば、3個の帽子と4個のコート、いくつの異なる衣装?; 12人のお菓子は4人の子供の間で均等に共有され、4人のケーキは8人の子供の間で均等に共有された)。
ディビジョン活動3年目
これはレッスン自体をカバーするものではありませんが、この段階で概念的な理解を持ってディビジョンをどのように教 このための前提条件は、関連する除算を教える前に、関連する乗算の事実を最初に教えることです。
構造について考えるとき、学生の学習の旅のこの部分では、グループ化と共有に固執するのが最善です。 以下の例では、4で割ることを理解する学生の開発を見ていきます。 それは具体的な絵画的抽象的なアプローチに従います。
それは、多くの場合、分割で彼らの進歩を制限することができ、数の学生の理解です。 特に、グループ化と共有に関しては、全体から連続的に1つだけを奪うときにのみ使用します。
教育部門の最初から、教師は、生徒が偶数やその他の数の事実についてすでに知っていることに傾くべきであり、生徒が適切な数で数えることに進
カウンターは、乗算の概念的な理解を構築する際に学生が論文を使用するため、関連する除算の事実を実証するために使用できます。 質問のような、”4のどのように多くのグループがありますか?”そして、”どのように多くの各グループにありますか?”尋ねられるべきであり、答えはこれが分割をいかにに示すか関連しているべきである。
先生:カウンターはいくつありますか?
子供:四人
教師:良い。 これは4つのグループです。 どのように多くの四つのグループがありますか?
子供:一人
教師:優秀。 私たちは一つのグループに四つのカウンターを持っています。 4つのカウンターを1つのグループにグループ化しました。 私たちは何をしましたか?
子:四つのカウンターを一つのグループにグループ化しました。
我々は一つのグループに四つのカウンタをグループ化するとき、我々は一つで割った四つの数学的計算を行っています。 私たちはどのような計算をしましたか?
子:四を一で割ったもの。
先生:そして、私たちが四つを一つで割ったとき、答えは四つです。 四つを一つで割ったものは四つである。 四つを一つで割ったものは何ですか?
: 四つを一つで割ったものは四つである。
あなたはそれが次のためにどのように繰り返されるかを見ることができます:
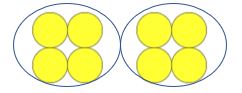
先生:カウンターはいくつありますか?
子供:八人
教師:良い、これは四人のグループです。 どのように多くの四つのグループがありますか?
子供:二人
教師:優秀。 私たちは一つのグループに四つのカウンターを持っています。 4つのカウンターを2つのグループにグループ化しました。 私たちは何をしましたか?
子:四つのカウンターを二つのグループにグループ化しました。
我々は二つのグループに四つのカウンタをグループ化するとき、我々は二つで割った八の数学的計算を行っています。 私たちはどのような計算をしましたか?
子供:八を二で割ったもの。
先生:そして、私たちが8を2で割ったとき、答えは4です。 八を二で割ったものは四である。 八を二で割ったものは何ですか?
子:八を二で割ったものは四です。
学生がこれに自信を持ち始めたら、Cuisenaire rodsなどの他のモデルに進むことができます。

ここでは、全体の量は、トップトレインで表され、紫色の棒(この場合には4を表し、あなたがうまくいけば、このシリーズの他のブログを読んでいる場合は、私が教室での使用のために午前どのくらいの支持者の知っているので、学生はそれまでにその値を認識することになります)は、合計金額に入ることができますどのように多くのグループを示すために使用されます4の。
その後、生徒は教師が読んだシナリオを描くことに進むことができます。 例えば。 そこに24のボタンがあり、彼らは4にグループ化する必要があります。 どのように多くのグループがありますか? 学生は、これらのボタンを描画し、4などにそれらをグループ化することができます。
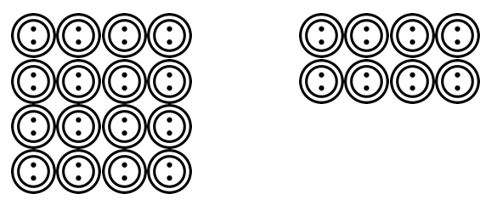
学生は、コンテキストの範囲内でこれらのグループ化または共有分割シナリオを視覚化することができることに慣れてきたら、彼らは数学的記号を使

3 年のための長い部門のワークシート3-6
これらの長い部門のワークシートでKS2を通して長い部門のために準備されたあなたの生徒を取得します。
Division Word Problems Year3
Year3のWord problemsは、一般的にグループ化または共有構造を使用します。
ケーキ40個、学生10人。 各学生はどのように多くのケーキを得るだろうか?
グループの数がわかっているので(10)、グループあたりの量を計算する必要があるので、これは共有構造です。 学生はこれを解決し、答え4を得るために4回表の知識を使用することが期待されます。
: 推論と問題解決3年目
推論と問題解決のために、私が見つけた良い活動は、単語の問題を計算に一致させることです。 例えば:
4で割った20を知ることによって解決されている単語の問題と一致します。
- 20個の鉛筆があり、それらは5個のパックに入れられます。 どのように多くの各パックですか?
- 20本の鉛筆があり、さらに4本の鉛筆を持ってくる生徒がいました。 今何本の鉛筆がありますか?
- 20個の鉛筆があり、4個のパックに入れられます。 どのように多くの各パックですか?
- 20本の鉛筆があり、その後4本が行方不明になった。 今何本の鉛筆がありますか?
それは彼らの思考を見ることができるように、各質問のための彼らの説明を書き留めるために学生を得ることは便利です。 各質問の数字が質問の数字に関連するように質問は慎重に選択されているので、学生は正しい答えを推測するために数学的スキルに頼っています。
Division Year4
イギリスの数学のための国家カリキュラムでは、概説されている数学の各分野には、法定要素と非法定要素の両方があります。 法定要素は次のとおりです:
- 12×12までの九九の乗算と除算の事実を思い出してください
- 0と1の乗算、1で除算、三つの数字の乗算
法定外の注意事項とガイダンスを含む、精神的に乗算と除算するために、既知および導出された事実を使用してください。:
- 生徒たちは、流暢さを助けるために掛け算の九九と関連する除算の事実を思い出し、使用する練習を続けています。
- 生徒は精神的な方法を練習し、これを3桁の数字に拡張して事実を導出します(たとえば、600÷3=200は2×3=6から導出できます)。
- 生徒は、正確な答えで短い乗算と短い除算の正式な書かれた方法に堪能になるために練習
- 生徒は、コンテキスト内の二段階の問題を解決し、適切な操作を選択し、ますます困難な数で作業します。 これには、メニュー上の食事の選択肢の数、または10人の子供の間で均等に共有される三つのケーキなどの対応の質問が含まれる必要があります。
Division Lesson Ideas Year4
このレッスンでは、それと一緒にマニピュラティブを使用して短いdivisionを教える方法を見ていきます。
私たちは質問168を12で割ったために学生に短い部門を教えるつもりだと言います。
通常、これは一般的にバス停と呼ばれるものに書いています。 しかし、興味深いのは、世界のさまざまな場所がそれを違った形で書いているということです。
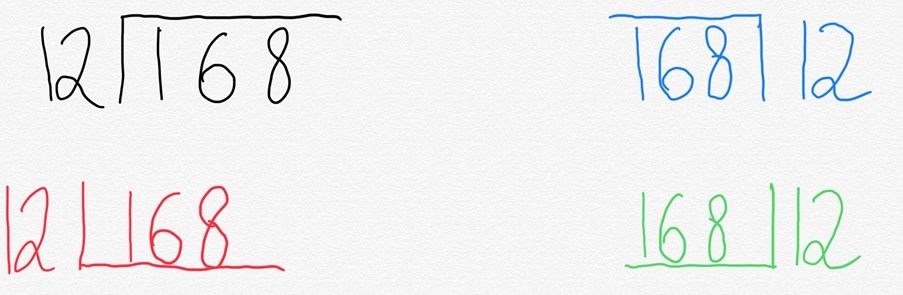
この理由は非常に簡単です。 ‘バス停’が実際に表すのは、長方形を表す短縮された方法です。
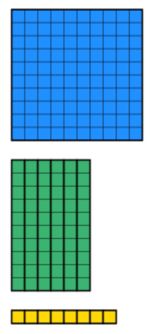
私たちが正式な短い除算を教えるとき、私たちが効果的に言っていることは、幅が12の長方形を想像する必要があるということです。 長方形の総面積は168であり、上部の欠落した長さを見つけようとしています。 では、どのようにマニピュレータを使用してこれを示すのですか? Dienesブロックは、このための便利なツールです。
私たちは合計金額が168であることを知っています。 だから我々は可能なブロックの最小量を使用してジエンの168の価値を収集する必要があります。 これを以下に示します。
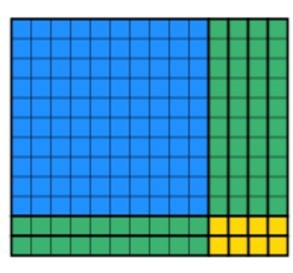
質問を振り返ってみると、幅は12であることがわかります。 つまり、幅が12になるようにブロックを操作する必要があります。 長方形は固体である必要があり、欠けている部分を持たないことに注意してください。 たとえば、幅を下る12単位があるにもかかわらず、以下は許可されません。
代わりに、学生は次のように2つの10sブロックを回転させることができます。 各列に12があり、それが固体のオブジェクトであることに注意してください。
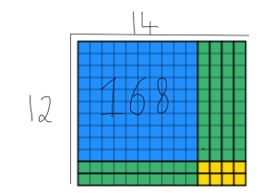
学生がしなければならない最後の部分は、幅12を維持しながら、販売された長方形を作成するために残りのブロックを使用しています。 これには時間がかかるかもしれませんが、練習では、学生はより速くなります。 しばらくすると、学生はこれを生成します:
私たちは、ブロックのすべての168の価値が使い果たされていることを見ることができ、幅はまだ12であること。 答えを見つけるには、学生は長さを数える必要があります。 私は以下の両方の方法を重ね合わせているので、それらがどのようにお互いを補完するかを見ることができます。
すでに学生に照らされているカリキュラムの他の分野で大規模な影響があるので、これは4年目の学生を教えるための有用な戦略です。
彼らはまだそれを認識していないかもしれませんが、このような短い分割を教えることによって、彼らはすでに周囲と面積に導入されています–こ それだけでなく、二次的には、このアプローチは代数的思考に移ります。
分割単語問題4年目
学生は、分割ベースの問題を解決するために場所価値の知識を引き出すことが期待されるので、適切な単語問題があります。
季節に4,800個のリンゴを栽培した果樹園。 彼らは市場に行く前に4つのパックに入れられます。 どのように多くのパックがありますか?
ここで、学生は4×12=48という事実を使用する必要があり、4,800は48よりも百倍であるため、12に100を掛けて1,200を得る必要があります
除算: 推論と問題解決4年目
3つの偶数の合計が4で割り切れることは、常に、時には、または決して真実ですか?
この質問は、学生に質問のパラメータ内で実験する機会を十分に与えます。 より多くのサポートを必要とする学生は歌う桁の偶数を見ることができ、学生は彼らが快適に感じるものは何でも上がることができます。
このような未解決の質問では、学生が何回の試みをすべきかについての最小要件を提供することは良いことです。
この質問に対する答えは時々あります。
数字が割り切れるかどうかを知るための簡単な”トリック”は、数字の最後の2桁を見て、それらが4で割り切れるかどうかを確認することです。 たとえば、子供が34、36、38の合計を見つけて108を得た場合、教師として、私はこの数字が4で割り切れることを知っています最後の2桁(08)が8を作り、4で割り 子供が118を得るために34、36、48を選んだ場合、これは4で割り切れないことを知っています18–118の最後の2桁–は4で割り切れません。
Division Year5
イギリスの数学のための国家カリキュラムでは、概説されている数学の各分野には、法定要素と非法定要素の両方があります。 法定要素は次のとおりです:
- 既知の事実に基づいて精神的に数字を乗算して除算する
- 4桁までの数字を短い除算の正式な書かれた方法を使用して一桁の数字で除算し、文脈に応じて剰余を適切に解釈する
- 整数と小数を含むものを10、100、1000で乗算と除算する
- 因子の知識を使用することを含む乗算と除算に関する問題を解決するそして、倍数、正方形、立方体
- は、加算、減算、乗算、除算、およびの組み合わせを含む問題を解決します 等号
- の意味を理解することを含むこれらは、単純な分数によるスケーリングや単純なレートを含む問題を含む乗算と除算を含む問題を解決します。
法定外の注意事項とガイダンス:
- 生徒は、剰余、分数、小数、または四捨五入(例えば、98÷4==24r2=24=24.5÷25)など、文脈に応じて異なる方法で結果を表現することによって、除算に対する非整数
- 生徒は、倍率の導入をサポートするために逆数として乗算と除算を使用します6,例えば、スケール図面で10の累乗で除算したり、キロメートルとメートルなどの単位間の変換で1,000の累乗で除算したりします。
5年目の課活動
5年目の課活動は、回答に剰余を使用することによって進行します。 このレッスンでは、私は教師が4×1桁の除算を教えるために使用できる別の使用マニピュレータを見ていきます。
質問が5,642を4で割った場合、以下に示すように、place value chartとplace value countersを使用してこれを表すことができます。
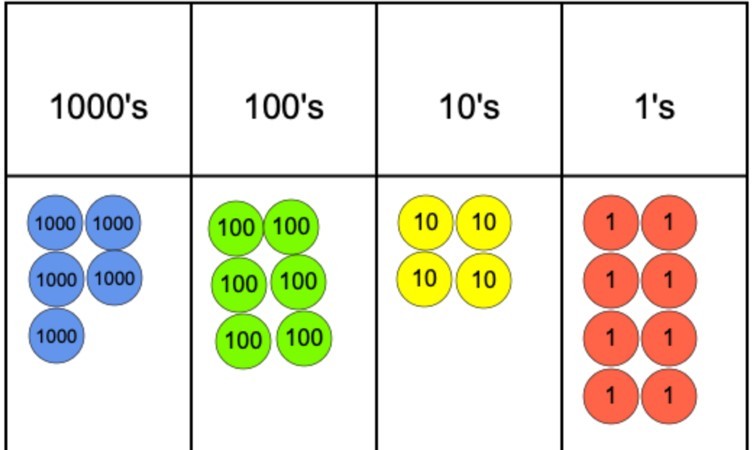
次のステップは、これが私たちの除数であるため、カウンタを4にグループ化し始めることです。 しかし、見ることができるように、我々はすぐに1000の列に問題が発生し、我々は4のグループに残りのカウンターをグループ化することはできませんが、その後、4のグループに残りのカウンターをすることができます。
この問題に対処するために、グループ化されていない1000カウンターを100カウンターと交換することができます。 これらは、4のグループにグループ化することができ、これは残って任意の100sカウンタが存在せずに発生する可能性があります。 そこから、それはその後、10年代に移動し、最終的にものの簡単なケースです。
1つのカウンターがあるので、それらのうち8つを2つのグループと4つにグループ化し、*の上に残っているものがあると主張することができます。 答えを見つけるには、必要なのは、各場所の値で作成されたグループの数を数え、これらを使用して最終的な答えを作成する桁を書くことだけです。 この場合、答えは1,412余り1になります。
※小数点以下を見ると、残りの1sカウンタを0.1カウンタに交換し、上記のように除算を続けることができます。 このモデルに精通している学生は、学生が苦労する可能性のある小数で除算を分かりやすくするのに役立つので便利です。 これは、彼らがすでに何か新しいものではなく、精通しているプロセスの継続であることを確認するのに役立ちます。
分割問題5年目
5年目に分割すると、学生は答えが文脈で意味をなさないように答えを丸める必要があるシナリオに遭遇します。 これを示す適切な質問は次のようなものです:
学校は、各学生に250mlのジュースを提供する予定の社交的な距離のあるディスコを計画しています。 彼らはジュースの2リットルのボトルを購入することができます。 彼らは33人の学生が到着することを期待しているので、8.25リットルのジュースを与えることを知っています。 どのように多くのジュースのボトルを購入する必要がありますか?
一般的な答えは、学生が4と四分の一を言うということです。 しかし、あなたはボトルの四分の一を購入することはできませんので、これは正しい答えは、すべての学生が参加できるようにするために必要とされるジュースの5本のボトルになりますインスタンスです。
部門:推論と問題解決5年目
上記のように、5年目には、答えを切り上げるかどうかを選択する必要がある部門内のシナリオに遭遇します。 たとえば、質問は、学校の旅行のために必要とされているどのように多くのバスを動作するように学生に尋ねたとき。
提供されたコンテキストの範囲を使用して学生が自分の問題を作成するようにすることは、学生がコンテキストと部門について数学的に考え
学生は、自分が作成した質問をパートナーと交換し、それらを解決し、正しい答えがあるかどうかを元の質問作成者に確認することができます。
Division Year6
イギリスの数学のための国家カリキュラムでは、概説されている数学の各分野には、法定要素と非法定要素の両方があります。 法定要素は次のとおりです:
- 長除算の形式的な表記法を用いて4桁までの数値を二桁の整数で除算し、剰余を整数の剰余、分数、または丸めとして解釈します。
- 4桁までの数値を短除算の形式的な表記法を用いて二桁の数値で除算します。
- コンテキストに応じて剰余を解釈します。混合演算や大きな数値を含む精神的な計算を行います。
- 共通因子、共通の倍数、素数を識別する
- 操作の順序に関する知識を使用して、四つの操作を含む計算を実行する
非法定ノートとガイダンス:
- 加算、減算、乗算、除算を含む問題を解決する
- 推定を使用して、計算に対する回答をチェックし、問題のコンテキストで適切な精度を決定します。
Division Lesson Ideas Year6
Sophie Bartlett(@_Missiebee)は、6年のクラスでlong divisionを教える方法を詳述した優れたブログをここに作成しました(Sophieのlong divisionを教えるブログへのリンク)。 Long divisionは6年目のdivisionに関する唯一の新しい学習であるため、これはlong divisionの手順を導入する理想的な方法です。
ディビジョンの質問6年目
6年目の学生が遭遇する典型的なディビジョンの単語問題は次のようになります。
学校はbake saleから£3,146を調達しました。 このイベントには104人の保護者が参加しました。 すべての親が同じ金額を費やした場合、各親はどれくらい費やしましたか?
ここで、学生はこの質問を解決するためにlong division methodを使用して£30.25の答えを得ることが期待されます。
部門:推論と問題解決6年目
長い部門のような手続き的なものでは、良い推論活動は学生に間違いを見つけさせることです。 これらのリソースは、そのような活動の大規模な銀行を提供します。 下の質問からわかるように、学生はすべてのハードワークを行っていますが、59のグループを数える際の不注意なエラーは、59×7が472であり、59×8ではないと
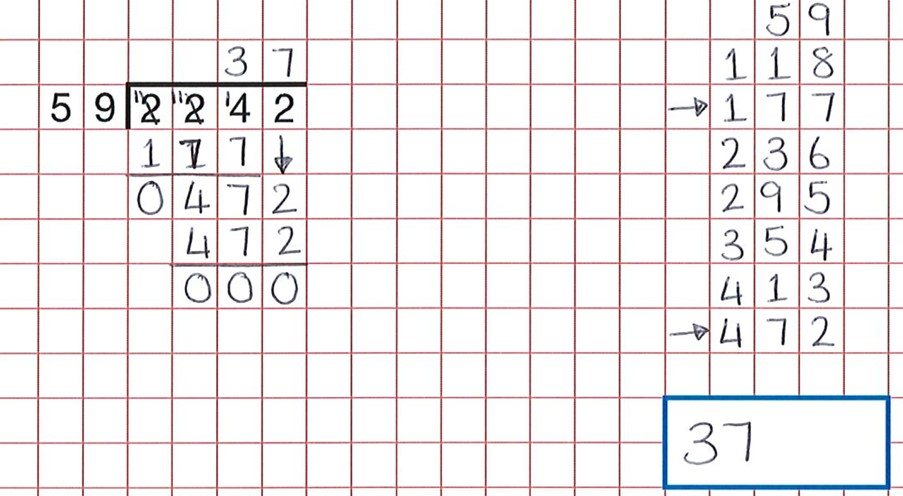
正解は38だったでしょう。
除算は、KS2だけでなく、数学全体で重要な数学のトピックです。 うまくいけば、この記事はあなたの生徒が自信を持ってそれに近づくのを助けるためにあなたにいくつかの良いアイデアを与えています。
学校や教師から信頼されるオンライン1対1の数学のレッスン
毎週Third Space Learningの数学の専門家のチューターは、毎週のオンライン1対1のレッスンと数学の介入で何千人もの小学校の子供たちをサポートしています。 2013年以来、100,000人以上の子供たちがより自信を持って、有能な数学者になるのを助けました。 続きを読むか、またはあなたの必要性についての私達に話すために個人化された引用を要求し、私達がいかに助けてもいいか。
小学校の授業料は、それぞれの子供のニーズを対象とし、密接に国家のカリキュラムに従っています。