このガイドでは、標準誤差式とは何か、それを使用して標準誤差を計算する方法を例を使用して説明します。
標準エラーとは何ですか？
標準誤差(SE)は、平均の標準誤差(SEM)とも呼ばれ、平均値に対するサンプリング分布の標準偏差に対応する統計量です。 しかし、それは実際には何ですか？
英国の平均年齢の人々がアルツハイマー病と診断されていることに興味があるとします。 英国のすべての人にとってこれを決定することは不可能であるため、研究者は全体的な数字を一般化するためにサンプル人口を取ります。 例えば、この疾患を有する10,000人の英国人を分析し、診断の平均年齢を生成するために使用することができる。 あなたは5,000人の患者の無作為サンプルでこれを行う場合は、61.5年の診断の平均年齢を得ることができます。 ただし、10,000人の他の患者の別のランダムサンプルでサンプル分析を行うと、平均年齢は62.3歳になる可能性があります。 たとえば、仮説的に言えば、実際の数字を得るためにアルツハイマー病を患っている英国のすべての人々を分析することができれば、64.3年になる可能性 サンプル母集団（61.5年と62.3年）から得られた数値は、実際の数値（64.3年）とは異なることに気付くことができます。 平均値のこの変動が予想され、サンプル母集団の人々の数を増やすと、実際の数値に近い値が得られます。 これはまさに標準エラーが表すものです。 標準誤差は、サンプル母集団間の平均値のこの変動を意味します。
さらに読むには、Douglas Altman教授とMartin Bland教授による短い統計ノートを読むことをお勧めします。 これは、標準誤差が何であり、標準偏差との違いが何であるかについての有用な洞察です。
標準誤差式
標準誤差を計算するには、標準偏差とデータセット内のサンプル数の二つの情報が必要です。 標準誤差は、標準偏差をサンプル数の平方根で除算することによって計算されます。
注釈付きの完全な標準エラー式は次のとおりです。
例
標準エラー式をよりよく理解するには、例を検討するのに役立ちます。 私たちは80人の人口を持っており、私たちは彼らの高さに興味があるとします。 彼らの高さを測定し、標準偏差を30.6cmとして計算します。 ここで、これらの値を式に差し込む必要があります:
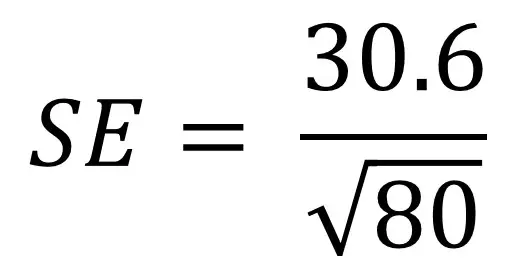電卓に方程式を入力することに不快な場合は、数式を管理可能なチャンクに分割することができます。 ここにあなたが取ることができるステップはある。
- まず、サンプル数（n）の平方根を計算します。 この場合、ｎは８ ０である。 80の平方根は8.94です。
- 次に、標準偏差(30.6)を80の平方根(8.94)で除算します。 これを行うと、3.42の値が得られます。
- したがって、私たちの身長に対する母集団の標準誤差は3.42cmです。