頂点、面、エッジは、子供たちが3d形状の特性について学んでいるときに小学校のジオメトリで多くのことを出てきます。 ここでは、これらのそれぞれが何を意味するのか、どのように任意の形状の頂点、面、エッジの数を計算するのかを説明します。 また、最も一般的な図形のエッジ、面、頂点の数も含めます。
この語彙は2年次の全国カリキュラムで導入されているため、小学校年間を通じて以下の情報を生徒に使用することができます。 あなたは彼らに頭のスタートを与えたい場合でも、年1の生徒は、このように形状の特性に従事し始めることができます!
図形の頂点とは何ですか?
図形の頂点は、2つ以上の線分または辺が交わる点です(角のように)。 頂点の特異点は頂点である。 たとえば、立方体には8つの頂点があり、円錐には1つの頂点があります。
頂点はコーナーと呼ばれることもありますが、2Dおよび3D形状を扱う場合は、頂点という言葉が優先されます。
立方体には8つの頂点があります。 ここには7つが表示され、1つは隠されています。
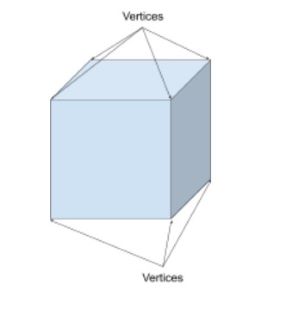
辺とは何ですか?
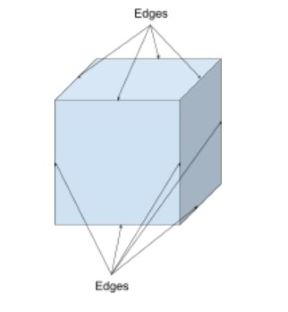
エッジは、ある頂点を別の頂点に結合する線分であり、シェイプの面が出会う場所でもあります。 これらは、2dおよび3d形状を記述するために使用することができます。
多くの図形は直線と直線のエッジを持っていますが、半球のような湾曲したエッジを持つ図形があります。 立方体には、以下に示すように12個の直線エッジがあり、9個が表示され、3個が非表示になります。

無料の3D図形独立した要約ワークシート
あなたの年2(および古い)生徒が私たちの無料の独立した要約ワークシートで頂点、顔やエッジを修正するのに役立
顔とは何ですか?
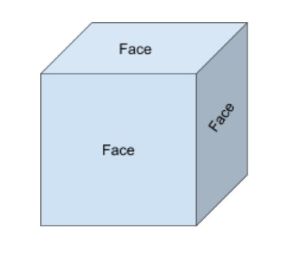
フェースは、ソリッドシェイプの平らな面です。 たとえば、直方体には6つの面があります。 2dおよび3d図形について考えるとき、2d図形は単に3d図形の顔を表すことを知っておくことが重要です。
私たちの現実は3次元で構成されているので、3次元の形に囲まれているので、2次元の形を物理的に扱うことは不可能であることを知っておく したがって、あなたの教室に”2d Shapes”というラベルの引き出しがある場合は、子供たちに誤解を教えているので、これを削除する必要があります。 教室のためのインタラクティブな概念が、2d形状は、2次元図面としてのみ存在することができます。
平らな面と湾曲した面の両方を持つことができますが、形状の視覚的によく一致するので、湾曲した面を湾曲した面として参照すると便利です。
下の立方体に表示されている三つの面と隠されている三つの面があります。
一般的な3d形状の頂点、面、エッジ
直方体にはいくつの面、辺、頂点がありますか?
直方体には8つの頂点があります。
直方体には12個の辺があります。
直方体には6つの面があります。

円柱にはいくつの面、辺、頂点がありますか?
円柱には0個の頂点があります。
シリンダーには2つのエッジがあります。
円柱は2つの面と1つの曲面を持っています。

半球にはいくつの面、辺、頂点がありますか?
半球には0個の頂点があります。
半球には1つの湾曲したエッジがあります。
半球は1つの面と1つの曲面を持っています。

円錐にはいくつの面、辺、頂点がありますか?
円錐には1つの頂点があります。
円錐には1つのエッジがあります。
半球は1つの面と1つの曲面を持っています。

四面体にはいくつの面、辺、頂点がありますか?
四面体には4つの頂点があります。
四面体には6つの辺があります。
四面体には4つの面があります。

球にはいくつの面、辺、頂点がありますか?
球には0個の頂点があります。
四面体には0個の辺があります。
四面体には1つの曲面があります。

プリズムにはいくつの面、辺、頂点がありますか?
プリズムは、両端の面が同じ形状である立体物、幾何学的形状または多面体です。 このように、学生は彼らの学校教育を通してプリズムの多くの種類に遭遇します。 共通の物は立方体、直方体、三角プリズム、五角形プリズムおよび六角形プリズムを含んでいます。
| 形状 | 絵 | 面 | 辺 | 頂点 |
|---|---|---|---|---|
| 三角プリズム | 5 | 9 | 6 | |
| 五角柱 | 7 | 15 | 10 | |
| 六角柱 | 8 | 18 | 12 | |
| Cube |  |
6 | 8 | 12 |
| 直方体 |  |
6 | 8 | 12 |
子供たちは小学校で頂点、面、エッジについて学ぶのはいつですか?
子供たちは幾何学を勉強するときに2年目に頂点、面、エッジの語彙を正式に導入する必要があります。 しかし、教師はこの語彙を以前に導入することを選択するかもしれません。
2年目:
- エッジ、頂点、面の数を含む3次元形状の特性を特定して記述する
非法定ガイダンスには、次のように記載されています:
- 生徒は、四角形や多角形、直方体、プリズム、円錐など、さまざまな一般的な2次元および3次元形状を処理し、名前を付け、各形状の特性(辺の数、面の数など)を識別します。 生徒は、その特性に基づいて形状を識別し、比較し、ソートし、辺、辺、頂点、面などの語彙を正確に使用します。
この時点から、全国のカリキュラムは頂点、面、エッジを明示的に参照していないため、他の年のグループの教師は、形状を見るときにこの語彙を使用し続けなければなりません
頂点、面、エッジは数学の他の領域とどのように関係していますか?
学生は、2d形状だけでなく、3d形状を見るときに頂点、面、エッジの知識を使用します。 エッジが何であるかを知り、複合形状上でそれらを識別することは、2d複合形状の周囲と面積を見つけるために重要です。 グラフ理論や放物線など、さまざまな数学の定理を扱う際には、後年の重要な基礎となります。
頂点、面、エッジは実際の生活とどのように関係していますか?
実際のオブジェクトは頂点、面、エッジを持っています。 例えば、結晶は八面体です–それは8つの面、12の辺と6つの頂点を持っています。 異なった三次元形のためのこれらの特性を知ることは建築、インテリア-デザイン、工学および多くのようなさまざまな企業の基礎を築く。
頂点、面、エッジの質問例
1. 頂点が何であるかを説明します。
(答え:頂点は2本の線が交わるところです)
2. 三角プリズムにはいくつのエッジがありますか?
(回答: 9)
3. 円錐にはいくつの頂点がありますか?
(回答:1件)
4件 直方体にはいくつの顔がありますか? これらの顔の2D形状は何ですか?
(答え:6人の顔。 それらは2つの正方形の表面および4つの長方形の表面またはちょうど6つの長方形の表面を持つことができます。)
5. すべての一般的なプリズム(立方体、直方体、三角形プリズム、五角形プリズム、六角形プリズム)について、面と頂点を一緒に追加し、エッジを減算します。 あなたは答えについて何に気づいていますか?
(答え:答えは常に2です。 これはオイラーの公式として知られています(頂点の数–辺の数+面の数=2)
あなたの子供に他の重要な数学の語彙を説明する方法について疑問に思 私たちの主要な数学の辞書をチェックアウト、またはこれらを試してみてください:
- 数学の習得とは何ですか?
- 2dシェイプとは何ですか?
- 3dシェイプとは何ですか?
Third Space Learning Maths Hubでは、小学生のためのジオメトリレッスンプランと印刷可能なワークシートをたくさん見つけることができます。
学校や教師から信頼されるオンライン1対1の数学のレッスン
毎週Third Space Learningの数学の専門家のチューターは、毎週のオンライン1対1のレッスンと数学の介入で何千人もの小学校の子供たちをサポートしています。 2013年以来、100,000人以上の子供たちがより自信を持って、有能な数学者になるのを助けました。 続きを読むか、またはあなたの必要性についての私達に話すために個人化された引用を要求し、私達がいかに助けてもいいか。
数学プログラムのための私たちのオンライン授業料は、独自のプロの一対一の数学の家庭教師を持つすべての子供を提供します