de afdeling in belangrijke fase 2 vormt het laatste deel van de “vier acties” – de vier fundamentele wiskundige concepten die leerlingen moeten kennen. Deze blog zal je helpen ervoor te zorgen dat al je leerlingen, van jaar 3 tot jaar 6, division kunnen benaderen met het vertrouwen dat ze nodig hebben om te slagen.
indeling in KS2-wiskunde bouwt voort op wat bij KS1 is geleerd. Tegen het einde van Y2 studenten aan de verwachte standaard in staat zal zijn om ‘herinneren en gebruik maken van vermenigvuldiging en deling feiten voor de 2, 5 en 10 vermenigvuldiging tabellen, met inbegrip van het herkennen van oneven en even getallen.”
voor leraren in jaar 3 is het altijd een goed idee om ervoor te zorgen dat de leerlingen deze zeer goed kennen. Daarmee bedoel ik niet alleen dat ze de tweedeling feiten naar je kunnen napraten, maar ze begrijpen echt hoe ze deze feiten moeten weergeven, zowel met concrete voorstellingen, verbale verklaringen als door middel van andere picturale methoden.
studenten die niet in staat zijn om dit te doen, maar wel in staat zijn om je mondeling de verdeling feiten te vertellen, hebben een zeer oppervlakkig begrip van verdeling en om verder te gaan met moeilijkere probleemoplossende activiteiten, is het verdiepen van hun conceptuele begrip van verdeling een must in jaar 3.
het nationale Curriculum plaatst de afdeling in dezelfde sectie als vermenigvuldiging voor de jaren 3-5 en plaatst deze in een sectie genaamd “vier operaties” in jaar 6. De delen uit het nationale Curriculum hebben alleen betrekking op de delen die specifiek betrekking hebben op division. De andere elementen van die secties zijn te vinden in de blog over vermenigvuldiging of optellen en aftrekken waar van toepassing.
Wat Is Division?
indeling is een van de vier bewerkingen – de vier wiskundige kernbegrippen die leerlingen moeten kennen – naast optellen en aftrekken en vermenigvuldigen.
wanneer vermenigvuldiging een getal meerdere keren combineert, is deling het tegenovergestelde: het berekenen van het aantal keren dat een getal binnen een ander getal zit. Bijvoorbeeld, het delen van 10 door 2 is de vraag hoeveel keer 2 is opgenomen in 10.

uit de online wiskundige interventies van Third Space Learning.
onderwijsafdeling KS2-de theorie
verdeling is de inverse van vermenigvuldiging. Net als bij de vermenigvuldiging blog, het onderwijs van divisie bevat drie onderliggende structuren, die, in combinatie met divisie feiten en conceptueel begrip studenten de beste kans om succesvol te zijn bij het oplossen van problemen met betrekking tot Divisie geven.
de drie structuren zijn delen, groeperen en schalen. Hoewel er niet genoeg tijd is om deze in de diepte te onderzoeken, zal wat volgt slechts een korte introductie tot hen zijn.
delen en groeperen zijn de inverse van vermenigvuldiging als herhaalde optelling. Delen is een structureel concept dat wordt geïntroduceerd in KS1 en eerder waar, zoals de naam al doet vermoeden, een bedrag wordt gedeeld in gelijke groepen.
bijvoorbeeld, 12 appels worden gedeeld door 3 studenten. Hoeveel appels krijgt elke student? Hier weten we het hele bedrag (12 appels) en cruciaal, we weten hoe het bedrag dat we gaan delen in (3). Afhankelijk van waar studenten zijn op hun wiskundige reis, kunnen ze herhaaldelijk aftrekken met een aantal (1, 2, 3 of 4) van het bedrag in drie stapels die de drie studenten vertegenwoordigen.
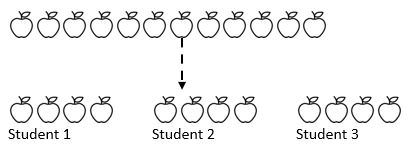
zoals we uit het bovenstaande kunnen zien, is het hele bedrag verdeeld in drie gelijke groepen.
groeperen is vergelijkbaar met delen, maar wat we weten is iets anders in vergelijking met delen. In de sharing structuur weten we hoeveel groepen het delen zal plaatsvinden. In de groepsstructuur weten we de hoeveelheid in elke groep, maar niet het aantal werkelijke groepen dat er zijn.
bijvoorbeeld, 12 appels worden gedeeld in groepen van 4. Hoeveel groepen zullen er zijn? Hoewel deze vraag zeer vergelijkbaar is met de bovenstaande, neemt het nu de structuur van de groepering aan omdat we weten hoeveel er in elke groep zullen gaan, maar niet meer weten hoeveel groepen er nu zullen zijn.
omdat we weten dat er 4 in elke groep zijn, kunnen we 4 appels groeperen totdat we alle 12 hebben behandeld om te zien dat er 3 groepen zijn.
de uiteindelijke structuur van de deling is schalen. Terwijl we in vermenigvuldiging een waarde opschalen, schaalt de deelstructuur naar beneden. Shannen heeft bijvoorbeeld 6 pennen en Jen 3 keer minder. Hoeveel pennen heeft Jen?
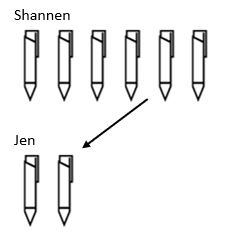
hier kunnen we zien dat om het totale aantal pennen te vinden dat Jen heeft, we de hoeveelheid die Shannen had moesten nemen en het met een schaalfactor van 3 moesten verlagen zodat Jen 2 pennen krijgt.
uit ervaring is dit de moeilijkste indeling voor studenten om te begrijpen en te begrijpen en is er een die moet worden herzien in combinatie met schalen als vermenigvuldiging, aangezien dit een cruciale vaardigheid is bij het omzetten van metingen en valuta ‘ s van een groter bedrag naar een kleiner bedrag. Bijvoorbeeld kilometers naar mijlen.
Afdelingsjaar 3
in het nationale Curriculum voor wiskunde in Engeland is er voor elk beschreven wiskundegebied zowel een statutair element als een niet-statutair element. Het statutaire element is als volgt::
- Recall and use vermenigvuldiging en deling feiten voor de 3, 4 en 8 vermenigvuldigingstabellen
- schrijf en bereken wiskundige verklaringen voor vermenigvuldiging en deling met behulp van de vermenigvuldigingstabellen die zij kennen, inclusief voor tweecijferige getallen maal ééncijferige getallen, gebruikmakend van mentale en voortschrijdende formele geschreven methoden
- los problemen op, inclusief problemen met ontbrekende getallen, met vermenigvuldiging en deling, inclusief problemen met positieve Schaalverdeling en correspondentieproblemen waarbij n-objecten zijn verbonden met m-objecten.
niet-statutaire toelichtingen en richtsnoeren:
- leerlingen ontwikkelen efficiënte mentale methoden, bijvoorbeeld met behulp van commutativiteit en associativiteit (bijvoorbeeld, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) en vermenigvuldiging en deling feiten (bijvoorbeeld, met behulp van 3 × 2 = 6, 6 ÷ 3 = 2 en 2 = 6 ÷ 3) om gerelateerde feiten af te leiden (bijvoorbeeld, 30 × 2 = 60, 60 ÷ 3 = 20 en 20 = 60 ÷ 3).
- leerlingen ontwikkelen betrouwbare geschreven methoden voor vermenigvuldiging en deling, te beginnen met de berekeningen van tweecijferige getallen met ééncijferige getallen en verder te gaan naar de formele geschreven methoden van korte vermenigvuldiging en deling.
- leerlingen lossen eenvoudige problemen op in contexten, waarbij ze beslissen welke van de vier operaties te gebruiken en waarom. Deze omvatten het meten en schalen van contexten (bijvoorbeeld vier keer zo hoog, acht keer zo lang enz.) en correspondentieproblemen waarbij m-objecten zijn verbonden met n-objecten (bijvoorbeeld 3 hoeden en 4 jassen, hoeveel verschillende outfits?; 12 snoepjes gelijk gedeeld tussen 4 kinderen; 4 gebakjes gelijk gedeeld tussen 8 kinderen).
Afdelingsactiviteiten jaar 3
dit zal geen les op zich omvatten, maar een leidraad vormen voor hoe indeling in dit stadium met enig conceptueel begrip kan worden onderwezen. Een eerste vereiste hiervoor zou het onderwijzen van verwante vermenigvuldigingsfeiten eerst zijn voordat het onderwijzen van een verwante verdeling.
bij het denken over structuren is het het beste om in dit deel van het leertraject van studenten te blijven groeperen en delen. Voor de volgende voorbeelden, zullen we kijken naar het ontwikkelen van studenten begrip van delen door 4. Het zal de Concrete-picturale-abstracte benadering volgen.
het is vaak het inzicht van studenten in het aantal dat hun vooruitgang in de indeling kan beperken. Vooral als het gaat om groeperen en delen als ze er maar één continu van het geheel wegnemen.
vanaf het begin van de onderwijsafdeling moeten leraren leunen op wat studenten al weten over even nummers en andere cijferfeiten om studenten te laten tellen in welk getal dan ook.
tellers kunnen worden gebruikt om gerelateerde splitsingsfeiten aan te tonen, aangezien studenten scripties zullen hebben gebruikt bij het opbouwen van hun conceptueel begrip van vermenigvuldiging. Vragen als: ‘hoeveel groepen van 4 zijn er?’en’ hoeveel zijn er in elke groep?’moet worden gevraagd en de antwoorden moeten betrekking hebben op hoe dit toont verdeeldheid.
leraar: hoeveel tellers zijn er?
Kind: Vier
Leraar: Goed. Dit is een groep van vier. Hoeveel groepen van vier zijn er?
Kind: Één
Leraar: Uitstekend. We hebben vier tellers in één groep. We hebben vier tellers in één groep gegroepeerd. Wat hebben we gedaan?
kind: vier tellers in één groep gegroepeerd.
Leraar: Briljant. Wanneer we vier tellers groeperen in één groep hebben we de wiskundige berekening gedaan van vier gedeeld door één. Welke berekening hebben we gedaan?
Kind: Vier gedeeld door één.
leraar: en als we vier oplossen gedeeld door één is het antwoord vier omdat we een groep hebben gemaakt die vier items bevat. Vier gedeeld door één is vier. Wat is vier gedeeld door één?
kind: Vier gedeeld door één is vier.
leraar: uitstekend
u kunt zien hoe dat zou worden herhaald voor de volgende:
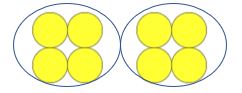
leraar: hoeveel tellers zijn er?
kind: acht
leraar: goed, Dit is een groep van vier. Hoeveel groepen van vier zijn er?
Kind: Twee
Leraar: Uitstekend. We hebben vier tellers in één groep. We hebben vier tellers in twee groepen gegroepeerd. Wat hebben we gedaan?
kind: vier tellers in twee groepen gegroepeerd.
Leraar: Briljant. Wanneer we vier tellers groeperen in twee groepen hebben we de wiskundige berekening gedaan van acht gedeeld door twee. Welke berekening hebben we gedaan?
kind: acht gedeeld door twee.
leraar: en als we acht oplossen gedeeld door twee is het antwoord vier omdat we twee groepen hebben gemaakt die vier items bevatten. Acht gedeeld door twee is vier. Wat is acht gedeeld door twee?
kind: acht gedeeld door twee is vier.
leraar: uitstekend
wanneer studenten hiermee vertrouwen beginnen te krijgen, kunnen we verder gaan met andere modellen zoals Cuisenaire rods.

hier is het hele bedrag is vertegenwoordigd in de top trein en de paarse staaf (die in dit geval vertegenwoordigt 4 en als je hebt gelezen andere blogs in deze serie hopelijk weet je hoeveel van een advocaat Ik ben voor het gebruik ervan in de klas en dus zullen studenten zich bewust zijn van de waarde ervan tegen die tijd) wordt gebruikt om te laten zien hoeveel groepen van 4 kan gaan in het totale bedrag.
leerlingen kunnen vervolgens scenario ‘ s uittekenen die door de leraar worden gelezen. Bijvoorbeeld. Er zijn 24 knoppen en ze moeten worden gegroepeerd in 4. Hoeveel groepen zijn er? Studenten konden deze knoppen te trekken en groeperen ze in 4 etc.
zodra de studenten gewend zijn geraakt aan het kunnen visualiseren van deze groeperen of delen van deling scenario ‘ s in een scala van contexten, dan kunnen ze overgaan tot meer abstracte voorstellingen met behulp van wiskundige symbolen.

3 Lange Divisie werkbladen voor jaren 3-6
maak uw leerlingen klaar voor lange divisie in KS2 met deze lange divisie werkbladen.
Deelwoordproblemen jaar 3
woordproblemen in jaar 3 zullen gewoonlijk gebruik maken van de structuur voor groeperen of delen.
er zijn 40 taarten en 10 studenten. Hoeveel taarten zou elke student krijgen?
omdat we weten hoeveel groepen er zijn (10) moeten we de hoeveelheid per groep berekenen, dus dit is een structuur voor delen. Van studenten wordt verwacht dat ze hun kennis van de 4 times table gebruiken om dit uit te werken en het antwoord te krijgen 4.
afdeling: Redeneren en probleemoplossing jaar 3
voor redeneren en probleemoplossing vind ik een goede activiteit om een woordprobleem aan een berekening te koppelen. Bijvoorbeeld::
overeenkomen met het woord problemen die worden opgelost door te weten 20 gedeeld door 4.
- er zijn 20 potloden die in verpakkingen van 5 potloden worden geplaatst. Hoeveel in elke verpakking?
- er waren 20 potloden en dan brengt een student er nog 4 bij. Hoeveel potloden zijn er nu?
- er zijn 20 potloden en ze worden in verpakkingen van 4 geplaatst. Hoeveel in elke verpakking?
- er waren 20 potloden en toen verdwenen er 4. Hoeveel potloden zijn er nu?
het is nuttig om studenten hun uitleg voor elke vraag te laten opschrijven, omdat ze hun denken kunnen zien. De vragen zijn zorgvuldig geselecteerd, zodat de nummers in elke vraag betrekking hebben op de nummers op de vraag, zodat studenten vertrouwen op hun wiskundige vaardigheden om het juiste antwoord af te leiden.
Afdelingsjaar 4
in het nationale Curriculum voor wiskunde in Engeland is er voor elk beschreven wiskundegebied zowel een statutair element als een niet-statutair element. Het statutaire element is als volgt::
- vermenigvuldigings – en delingsfeiten terugroepen voor vermenigvuldigingstabellen tot 12 × 12
- plaatswaarde, bekende en afgeleide feiten gebruiken om mentaal te vermenigvuldigen en te delen, waaronder: vermenigvuldigen met 0 en 1; delen door 1; drie getallen
samen vermenigvuldigen:
- leerlingen oefenen nog steeds met het herinneren en gebruiken van vermenigvuldigingstabellen en gerelateerde splitsingsfeiten om vlotheid te bevorderen.
- leerlingen oefenen mentale methoden uit en breiden dit uit tot driecijferige getallen om feiten af te leiden (bijvoorbeeld 600 ÷ 3 = 200 kan worden afgeleid uit 2 x 3 = 6).
- leerlingen oefenen om vloeiend te worden in de formele schriftelijke methode van korte vermenigvuldiging en korte deling met exacte antwoorden
- leerlingen lossen problemen in twee stappen op in contexten, kiezen de juiste operatie, werken met steeds moeilijker aantallen. Dit moet ook correspondentie vragen zoals het aantal keuzes van een maaltijd op een menu, of drie gebak gelijk gedeeld tussen 10 kinderen.
indeling lesideeën jaar 4
voor deze les zal ik kijken hoe u kunt beginnen met het onderwijzen van korte verdeling met behulp van manipulatieven ernaast.
zeggen dat we de studenten een korte verdeling voor vraag 168 gaan geven gedeeld door 12.
normaal schrijven we dit in wat gewoonlijk bushalte wordt genoemd. Maar wat interessant is, is dat verschillende plaatsen in de wereld het anders schrijven.
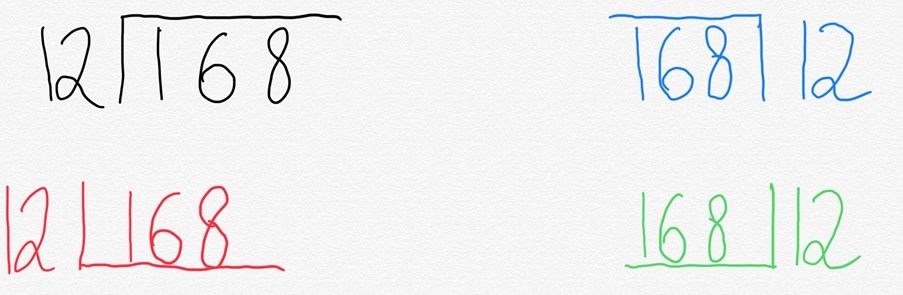
de reden hiervoor is vrij eenvoudig. Wat de ‘bushalte’ eigenlijk voorstelt is een verkorte manier om een rechthoek weer te geven.
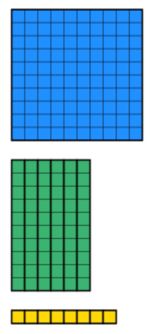
wanneer we formele korte deling onderwijzen, zeggen we in feite dat je je een rechthoek moet voorstellen met een breedte van 12. De totale oppervlakte van de rechthoek is 168 en we proberen de ontbrekende lengte over de bovenkant te vinden. Hoe laten we dit zien met manipulatieve middelen? Dienenblokken zijn hiervoor een nuttig hulpmiddel.
we weten dat het totale bedrag 168 is. Dus we moeten 168 waarde van dienes te verzamelen met behulp van de kleinste hoeveelheden blokken mogelijk. Dit wordt hieronder weergegeven.
Terugkijkend op de vraag, weten we dat de breedte 12 is. Dat betekent dat we nu de blokken moeten manipuleren zodat we een breedte van 12 krijgen. Merk op dat de rechthoek solide moet zijn en geen ontbrekende delen mag hebben. Bijvoorbeeld, de onderstaande zou niet worden toegestaan ondanks dat er 12 eenheden naar beneden de breedte.
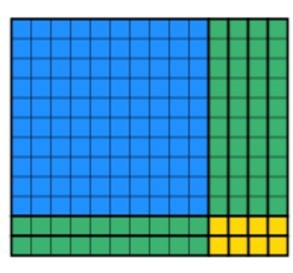
in plaats daarvan kunnen studenten twee 10s blokken roteren om het volgende te krijgen. Merk op dat er 12 in elke kolom en het is een vast object.
het laatste deel dat de leerlingen moeten doen is de resterende blokken gebruiken om een verkochte rechthoek te maken met behoud van de breedte 12. Dit kan enige tijd duren, maar met de praktijk, studenten sneller. Na enige tijd zullen studenten dit produceren:
We kunnen zien dat alle 168 ter waarde van blokken zijn opgebruikt en dat de breedte is nog steeds 12. Om het antwoord te vinden, moeten studenten de lengte tellen, die in dit geval 14 is. Ik heb beide methoden onder gelegd, zodat u kunt zien hoe ze elkaar aanvullen hieronder.
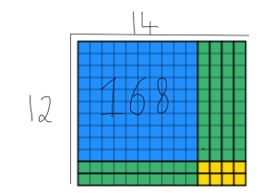
Dit is een nuttige strategie om studenten in jaar 4 te onderwijzen, omdat er enorme gevolgen zijn op andere gebieden van het curriculum die al verlicht zijn voor studenten.
hoewel ze het misschien nog niet herkennen, zijn ze door het onderwijzen van een korte indeling als deze al geïntroduceerd in perimeter en gebied – bedenk hoeveel leertijd kan worden bespaard wanneer deze verbinding wordt gemaakt. Niet alleen dat, maar in het secundair gaat deze benadering over op algebraïsch denken.
problemen met Afdelingswoorden jaar 4
van studenten wordt verwacht dat zij gebruik maken van hun kennis van plaatswaarde om op afdelingsproblemen gebaseerde problemen op te lossen en dus zou een passend woordprobleem zijn.
een boomgaard met 4.800 appels per seizoen. Ze worden in verpakkingen van 4 geplaatst voordat ze naar de markt gaan. Hoeveel pakjes zijn er?
hier moeten studenten gebruik maken van het feit dat 4 x 12 = 48 en aangezien 4,800 honderd keer meer is dan 48, moet 12 ook met vermenigvuldigd met 100 om 1.200
verdeling te krijgen: Redeneren en probleemoplossing jaar 4
is het altijd, soms of nooit waar dat de som van drie even getallen deelbaar is door 4?
deze vraag biedt studenten ruime mogelijkheden om binnen de parameters van de vraag te experimenteren. Studenten die meer steun nodig hebben kunnen kijken naar sing digit even numbers en studenten kunnen gaan naar wat ze zich comfortabel voelen met.
bij open vragen als deze, is het goed om een minimumvereiste te geven voor hoeveel pogingen studenten moeten doen anders zullen ze vaak kiezen om het absolute minimum te doen.
het antwoord op deze vraag is soms.
een snelle ’truc’ om te weten of een getal deelbaar is, is om naar de laatste 2 cijfers van het getal te kijken en te zien of deze deelbaar zijn door 4. Als een kind bijvoorbeeld de som van 34, 36 en 38 vond en 108 kreeg, Weet ik als leraar dat dit getal deelbaar is door 4 omdat de laatste twee cijfers (08) 8 zijn en deelbaar zijn door 4. Als een kind 34, 36 en 48 kiest om 118 te krijgen, Weet ik dat dit niet deelbaar is door 4 als 18 – de laatste twee cijfers van 118 – zijn niet deelbaar door 4.
Afdelingsjaar 5
in het nationale Curriculum voor wiskunde in Engeland is er voor elk beschreven wiskundegebied zowel een statutair element als een niet-statutair element. Het statutaire element is als volgt::
- Vermenigvuldigen en te delen, nummers mentaal op basis van bekende feiten
- deel getallen tot 4 cijfers in met een één-cijferig nummer in met de formele schriftelijke methode van korte divisie en interpreteren van restanten passend voor de context
- Vermenigvuldigen en delen van hele getallen en die waarbij de decimalen worden door 10, 100 en 1000
- het Oplossen van problemen met vermenigvuldiging en deling met inbegrip van het gebruik van hun kennis van de factoren en veelvouden, vierkanten en kubussen
- het Oplossen van problemen met optellen, aftrekken, vermenigvuldigen en delen en een combinatie van deze, met inbegrip van het begrijpen van de Betekenis van het gelijken teken
- lossen problemen met vermenigvuldiging en deling op, met inbegrip van schalen door eenvoudige breuken en problemen met eenvoudige rates.
niet-statutaire toelichtingen en richtsnoeren:
- leerlingen interpreteren niet-integer antwoorden op deling door resultaten op verschillende manieren uit te drukken, afhankelijk van de context, inclusief met restanten, als breuken, als decimalen of door afronding (bijvoorbeeld 98 ÷ 4 = = 24 r 2 = 24 = 24,5 ≈ 25).
- leerlingen gebruiken vermenigvuldiging en deling als inverse om de invoering van ratio in jaar 6 te ondersteunen, bijvoorbeeld door te vermenigvuldigen en te delen door bevoegdheden van 10 in schaaltekeningen of door te vermenigvuldigen en te delen door bevoegdheden van 1000 in omrekening tussen eenheden zoals kilometers en meters.
afdeling activiteiten jaar 5
afdeling in jaar 5 vordert door het gebruik van restanten in antwoorden. Voor deze les, zal ik kijken naar een ander gebruik manipulatieven die leraren kunnen gebruiken om te onderwijzen 4-door-1-cijferige verdeling.
als de vraag 5,642 gedeeld door 4 was, zouden we dit kunnen weergeven met behulp van een plaatswaardegrafiek en plaatswaardetellers zoals we hieronder kunnen zien.
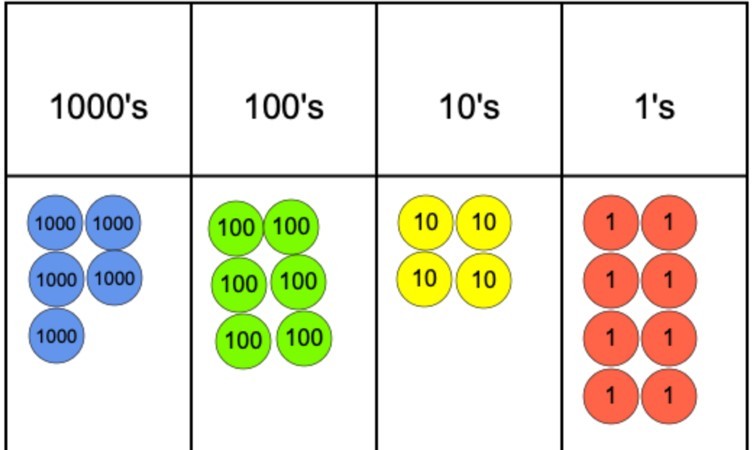
de volgende stap zou zijn om te beginnen met het groeperen van de tellers in 4 omdat dit onze deler is. Echter, zoals te zien is, komen we snel tot een probleem in de kolom 1000 omdat we in staat zijn om 4 van de tellers te groeperen, maar dan kunnen we de resterende teller niet groeperen in een groep van 4.
om dit probleem te bestrijden, kan de 1000 teller die niet is gegroepeerd, worden geruild voor tien 100 tellers. Deze kunnen dan worden gegroepeerd in groepen van 4 en dit kan gebeuren zonder dat er 100s tellers overblijven. Vanaf daar, het is een eenvoudig geval van Dan verhuizen naar de 10 ‘ s en uiteindelijk degenen.
omdat er negen 1s tellers zijn, kunnen we 8 van hen groeperen in 2 groepen en 4 en beweren dat er één over is*. Om het antwoord te vinden, alles wat nodig is om het aantal groepen gemaakt in elke plaats waarde tellen en deze gebruiken om de cijfers te schrijven om het uiteindelijke antwoord te maken. In dit geval zou het antwoord 1,412 rest 1.
* wanneer u naar decimalen kijkt, kunt u de resterende 1s teller inruilen voor tien 0.1 tellers en de verdeling voortzetten zoals hierboven beschreven. Studenten die bekend zijn met dit model is nuttig omdat het kan helpen om verdeeldheid te demystificeren met decimalen waarmee studenten kunnen worstelen. Dit helpt hen te zien dat het een voortzetting is van een proces dat ze al kennen in plaats van iets nieuws.
deelproblemen jaar 5
bij de verdeling in jaar 5 komen studenten scenario ‘ s tegen waarin ze hun antwoord moeten afronden om het antwoord zinvol te maken in de context. Een passende vraag die dit aantoont zou ongeveer de volgende zijn:
een school plant een discotheek op sociale afstand waar ze van plan zijn om elke student 250 ml sap aan te bieden. Ze kunnen 2 liter flessen sap kopen. Ze verwachten 33 studenten te komen dus weet dat zal geven 8,25 liter sap. Hoeveel flessen sap moeten ze kopen?
een algemeen antwoord is dat studenten zeggen 4 en een kwart. Echter, als je niet kunt kopen een kwart van een fles, in dit geval het juiste antwoord zou zijn 5 flessen sap nodig zou zijn om ervoor te zorgen dat alle studenten kunnen deelnemen.
afdeling: redeneren en probleemoplossing jaar 5
zoals hierboven vermeld, zullen studenten in jaar 5 scenario ‘ s tegenkomen binnen de afdeling waar zij moeten kiezen of een antwoord naar boven of naar beneden moet worden afgerond. Bijvoorbeeld, wanneer een vraag vraagt studenten om uit te werken hoeveel bussen nodig zijn voor een school een reis.
studenten hun eigen problemen laten creëren met behulp van een reeks van gegeven context kan een echt uitdagende activiteit zijn die de studenten wiskundig laat nadenken over context en verdeling.
studenten kunnen dan de door hen gemaakte vragen ruilen met een partner en ze vervolgens oplossen en met de oorspronkelijke vraagmaker controleren of ze het juiste antwoord hebben.
Afdelingsjaar 6
in het nationale Curriculum voor wiskunde in Engeland is er voor elk beschreven wiskundegebied zowel een statutair element als een niet-statutair element. Het statutaire element is als volgt::
- deel getallen tot 4 cijfers in met een twee-cijferig hele nummer met behulp van de formele schriftelijke methode van lange divisie en interpreteren van restanten als geheel aantal restanten, breuken, of door een afronding, afhankelijk van de context
- deel getallen tot 4 cijfers met een getal van twee cijfers met behulp van de formele schriftelijke methode van korte divisie waar van toepassing, de interpretatie van restanten volgens de context
- uitvoeren mentale berekeningen, ook met gemengde activiteiten en grote aantallen
- identificeren van gemeenschappelijke factoren, gemeenschappelijke veelvouden en priemgetallen
- hun kennis van de volgorde van de verrichtingen gebruiken om berekeningen uit te voeren met betrekking tot de vier verrichtingen
niet-statutaire toelichtingen en richtsnoeren:
- Los problemen op met optellen, aftrekken, vermenigvuldigen en delen
- gebruik schattingen om antwoorden op berekeningen te controleren en in de context van een probleem een passende mate van nauwkeurigheid te bepalen.
Divisie lesideeën jaar 6
Sophie Bartlett (@_MissieBee) heeft hier een uitstekende blog gemaakt (link naar Sophie ‘ s blog over het onderwijzen van lange divisie) waarin wordt beschreven hoe ze lange divisie zou onderwijzen voor een jaar 6 klas. Aangezien lange divisie het enige nieuwe leren over divisie voor jaar 6 is, is dit een ideale manier om de procedure van lange divisie te introduceren.
Afdelingsvragen jaar 6
een typisch afdelingswoordprobleem dat een student van jaar 6 zou tegenkomen zou zijn:
een school haalde £3.146 op uit een bakverkoop. 104 ouders woonden het evenement bij. Als alle ouders evenveel geld uitgeven, hoeveel heeft elke ouder dan uitgegeven?
hier wordt van studenten verwacht dat ze de long division methode gebruiken om deze vraag op te lossen om het antwoord £30,25 te krijgen.
indeling: redeneren en probleemoplossing jaar 6
met iets procedurele zoals lange deling, is een goede redeneeractiviteit om leerlingen fouten te laten vinden. Deze middelen zorgen voor een grote bank van dergelijke activiteiten. Zoals we kunnen zien uit de vraag hieronder de studenten heeft al het harde werk gedaan, maar een onzorgvuldige fout in het tellen van de groepen van 59 betekent dat het kind geloofde 59 x 7 was 472 en niet 59 x 8.
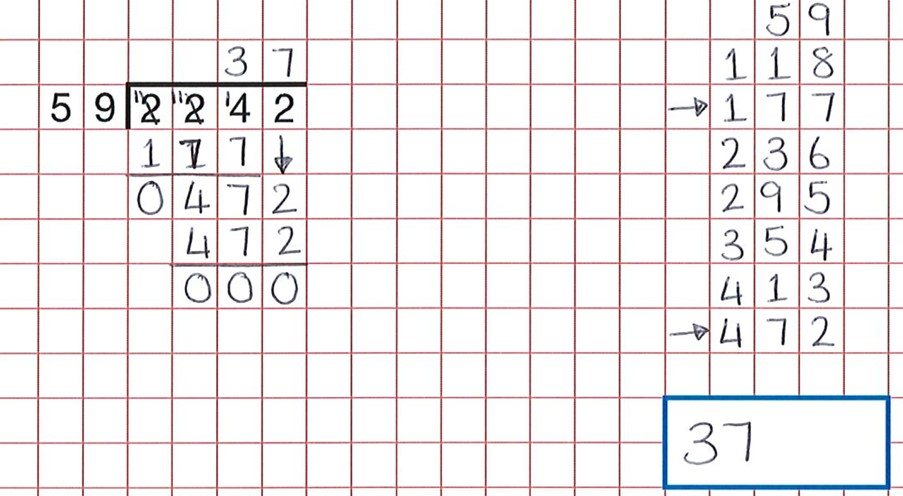
het juiste antwoord zou 38 zijn geweest.
deling is een belangrijk wiskundeonderwerp, niet alleen bij KS2, maar in wiskunde als geheel. Hopelijk heeft dit bericht je een aantal goede ideeën gegeven om je leerlingen te helpen het met vertrouwen te benaderen.
online 1-op-1 wiskundeles vertrouwd door scholen en leraren
elke week ondersteunen de wiskundespecialisten van Third Space Learning duizenden basisschoolkinderen met wekelijkse online 1-op-1 lessen en wiskundeinterventies. Sinds 2013 hebben we meer dan 100.000 kinderen geholpen om zelfverzekerder en bekwamer wiskundigen te worden. Meer informatie of Vraag een gepersonaliseerde offerte aan om met ons te praten over uw behoeften en hoe we u kunnen helpen.
basisschoolonderwijs gericht op de behoeften van elk kind en nauw volgens het nationale Curriculum.