hoekpunten, gezichten en randen komen veel voor in de geometrie van de lagere school wanneer kinderen leren over de eigenschappen van 3d-vormen. Hier leggen we uit wat elk van deze betekenen en hoe het aantal hoekpunten, gezichten en randen voor elke vorm uit te werken. We omvatten ook het aantal randen, gezichten en hoekpunten van de meest voorkomende vormen.
deze woordenschat wordt in jaar 2 in het nationale curriculum opgenomen, zodat de volgende informatie gedurende de gehele lagere schooljaren bij de leerlingen kan worden gebruikt. Zelfs leerlingen van jaar 1 kunnen op deze manier beginnen met eigenschappen van vormen als je ze een voorsprong wilt geven!
wat zijn hoekpunten in vormen?
hoekpunten in vormen zijn de punten waar twee of meer lijnsegmenten of randen elkaar ontmoeten (zoals een hoek). Het enkelvoud van hoekpunten is vertex. Een kubus heeft bijvoorbeeld 8 hoekpunten en een kegel heeft één hoekpunt.
hoekpunten worden soms hoeken genoemd, maar bij 2D-en 3D-vormen heeft het woord hoekpunten de voorkeur.
een kubus heeft 8 hoekpunten. 7 zijn hier zichtbaar en één is verborgen.
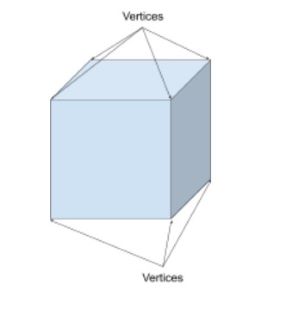
wat zijn randen?
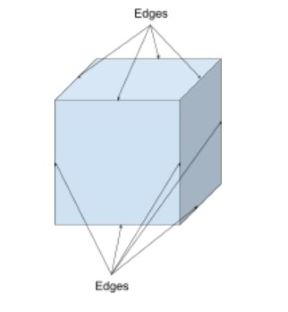
randen zijn de lijnsegmenten die de ene hoekpunt met de andere verbinden en zijn ook waar de vlakken van de vorm samenkomen. Deze kunnen worden gebruikt om 2d en 3d vormen te beschrijven.
hoewel veel vormen rechte lijnen en rechte randen hebben, zijn er vormen met gebogen randen, zoals een halve bol. Een kubus heeft 12 rechte randen zoals hieronder te zien; 9 zijn zichtbaar en 3 zijn verborgen.

FREE 3D Shapes Independent Recap werkbladen
Help uw leerlingen van jaar 2 (en ouder) om hoekpunten, gezichten en randen te herzien met onze gratis Onafhankelijke Recap werkbladen.
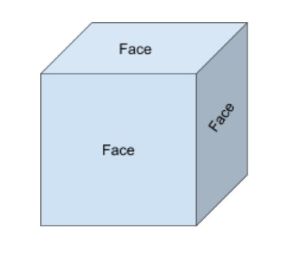
wat zijn gezichten?
vlakken zijn het vlakke oppervlak van een vaste vorm. Bijvoorbeeld, een cuboid heeft 6 gezichten. Bij het denken over 2d en 3d vormen, is het belangrijk om te weten dat een 2d vorm slechts het gezicht van een 3d vorm vertegenwoordigt.
het is ook belangrijk om te weten dat aangezien onze werkelijkheid in 3 dimensies is geconstrueerd, het onmogelijk is om 2D-vormen fysiek te hanteren omdat we omringd zijn door 3-dimensionale vormen. Daarom, als in uw klaslokaal is er een lade met het label ‘2d vormen’ dit moet worden verwijderd als het is het onderwijzen van kinderen een misvatting. Hoewel een interactief concept voor de klas, 2d vormen kunnen alleen bestaan als 2 dimensionale tekeningen.
u kunt zowel vlakke als gebogen gezichten hebben, maar ik vind het nuttig om naar gebogen gezichten te verwijzen als gebogen oppervlakken omdat het goed past bij het visuele van de vorm.
er zijn drie zichtbare gezichten en drie verborgen op de kubus hieronder.
hoekpunten, zijden en randen van gemeenschappelijke 3d-vormen
hoeveel vlakken, randen en hoekpunten heeft een kubus?
een kubus heeft 8 hoekpunten.
een balk heeft 12 randen.
een balk heeft 6 zijden.

hoeveel zijden, randen en hoekpunten heeft een cilinder?
een cilinder heeft 0 hoekpunten.
een cilinder heeft 2 randen.
een cilinder heeft 2 vlakken en 1 gebogen oppervlak.

hoeveel zijden, randen en hoekpunten heeft een halfrond?
een halfrond heeft 0 hoekpunten.
een halfrond heeft 1 gebogen rand.
een halfrond heeft 1 zijde en 1 gebogen oppervlak.

hoeveel vlakken, randen en hoekpunten heeft een kegel?
een kegel heeft 1 hoekpunt.
een kegel heeft 1 Rand.
een halfrond heeft 1 zijde en 1 gebogen oppervlak.

hoeveel zijden, randen en hoekpunten heeft een tetraëder?
een tetraëder heeft 4 hoekpunten.
een tetraëder heeft 6 randen.
een tetraëder heeft vier zijden.

hoeveel vlakken, randen en hoekpunten heeft een bol?
een bol heeft 0 hoekpunten.
een tetraëder heeft 0 randen.
een tetraëder heeft 1 gebogen oppervlak.

hoeveel vlakken, randen en hoekpunten heeft een prisma?
een prisma is een vast object, een geometrische vorm of een veelvlak waarbij de zijden van beide uiteinden dezelfde vorm hebben. Als zodanig, studenten zullen tegenkomen vele soorten prisma ‘ s tijdens hun opleiding. Veel voorkomende zijn kubussen, kubussen, driehoekige prisma ‘s, vijfhoekige prisma’ s en zeshoekige prisma ‘ s.
| Vorm | Afbeeldingen | Gezichten | Randen | Vertices |
|---|---|---|---|---|
| Driehoekige Prisma | 5 | 9 | 6 | |
| Vijfhoekige Prisma | 7 | 15 | 10 | |
| Zeshoekige Prisma | 8 | 18 | 12 | |
| Cube |  |
6 | 8 | 12 |
| Kubusvormige |  |
6 | 8 | 12 |
Wanneer leren de kinderen over hoekpunten, vlakken en randen en in de lagere school?
kinderen moeten formeel kennismaken met de woordenschat van hoekpunten, gezichten en randen in jaar 2 bij het bestuderen van geometrie. Leraren kunnen echter de keuze maken om deze woordenschat eerder in te voeren.
leerlingen van jaar 2 MOETEN in staat zijn om:
- Identificeer en beschrijf de eigenschappen van 3D-vormen, met inbegrip van het aantal randen, hoekpunten en zijden
de niet-wettelijke richtlijnen stellen dat:
- leerlingen behandelen en benoemen een breed scala van gemeenschappelijke 2-d en 3-d vormen, waaronder: vierhoeken en polygonen, en cuboids, prisma ‘ s en kegels, en identificeren de eigenschappen van elke vorm (bijvoorbeeld, aantal zijden, aantal gezichten). Leerlingen identificeren, vergelijken en sorteren vormen op basis van hun eigenschappen en gebruiken precies woordenschat, zoals zijkanten, randen, hoekpunten en gezichten.
vanaf dit punt wordt in het nationale curriculum niet meer expliciet verwezen naar hoekpunten, gezichten en randen, zodat leraren in andere jaargroepen deze woordenschat moeten blijven gebruiken wanneer ze kijken naar vorm
hoe verhouden hoekpunten, vlakken en randen zich tot andere wiskundige gebieden?
studenten zullen de kennis van hoekpunten, gezichten en randen gebruiken bij het bekijken van zowel 2d-als 3d-vormen. Weten wat randen zijn en het identificeren van hen op samengestelde vormen is cruciaal voor het vinden van de omtrek en het gebied van 2D samengestelde vormen. Het is een belangrijke basis voor latere jaren bij het omgaan met verschillende wiskundige stellingen, zoals grafentheorie en parabolen.
hoe verhouden hoekpunten, vlakken en randen zich tot het echte leven?
elk object in het echte leven heeft hoekpunten, vlakken en randen. Een kristal is bijvoorbeeld een octaëder-het heeft acht gezichten, twaalf randen en zes hoekpunten. Het kennen van deze eigenschappen voor verschillende driedimensionale vormen legt de basis voor verschillende industrieën zoals architectuur, interieur, engineering en meer.
hoekpunten, zijden en randen voorbeeldvragen
1. Leg uit wat een vertex is.
(antwoord: een hoekpunt is waar twee regels samenkomen)
2. Hoeveel randen heeft een driehoekig prisma?
(antwoord: 9)
3. Hoeveel hoekpunten heeft een kegel?
(antwoord: 1 vertex)
4. Hoeveel gezichten heeft een balk? Wat zijn de 2D-vormen van die gezichten?
(antwoord: 6 gezichten. Ze kunnen 2 vierkante gezichten hebben en 4 rechthoekige gezichten of slechts 6 rechthoekige gezichten.)
5. Voor alle gangbare prisma ’s (blokjes, blokjes, driehoekige prisma’ s, vijfhoekige prisma ’s en zeshoekige prisma’ s) voegen de vlakken en hoekpunten bij elkaar en trekken de randen af. Wat valt je op aan de antwoorden?
(antwoord: het antwoord is altijd 2. Dit staat bekend als de formule van Euler (aantal hoekpunten – aantal randen + aantal gezichten = 2)
vraagt u zich af hoe u andere belangrijke wiskundige woordenschat aan uw kinderen kunt uitleggen? Bekijk onze primaire Wiskunde Woordenboek, of probeer deze:
- Wat is wiskunde meesterschap?
- Wat zijn 2d-vormen?
- wat zijn 3d-vormen?
u kunt veel meetkundelesschema ‘ s en afdrukbare werkbladen voor basisschoolleerlingen vinden op de Third Space Learning Maths Hub.
online 1-op-1 wiskundeles vertrouwd door scholen en leraren
elke week ondersteunen de wiskundespecialisten van Third Space Learning duizenden basisschoolkinderen met wekelijkse online 1-op-1 lessen en wiskundeinterventies. Sinds 2013 hebben we meer dan 100.000 kinderen geholpen om zelfverzekerder en bekwamer wiskundigen te worden. Meer informatie of Vraag een gepersonaliseerde offerte aan om met ons te praten over uw behoeften en hoe we u kunnen helpen.
ons online collegegeld voor wiskunde-programma biedt elk kind zijn eigen professionele één-op-één wiskundeleraar