dział w kluczowym etapie 2 stanowi ostatnią część „czterech operacji” – czterech podstawowych pojęć matematycznych, które uczniowie powinni znać. Ten blog pomoże Ci upewnić się, że wszyscy twoi uczniowie, od roku 3 do roku 6, mogą podejść do sekcji z pewnością, której potrzebują, aby odnieść sukces.
podział w matematyce KS2 opiera się na tym, czego nauczyliśmy się w KS1. Pod koniec Y2 uczniowie w oczekiwanym standardzie będą mogli ” przypomnieć i wykorzystać fakty mnożenia i dzielenia dla tablic mnożenia 2, 5 i 10, w tym rozpoznawania liczb nieparzystych i parzystych.”
dla nauczycieli w 3 roku zawsze dobrym pomysłem jest upewnienie się, że uczniowie dobrze je znają. Przez to nie mam na myśli po prostu tego, że mogą papugować fakty podziału na ciebie, ale naprawdę rozumieją, jak reprezentować te fakty zarówno za pomocą konkretnych reprezentacji, wyjaśnień słownych, jak i za pomocą innych metod obrazowych.
uczniowie, którzy nie są w stanie tego zrobić, ale są w stanie werbalnie powiedzieć ci fakty dotyczące podziału, mają bardzo płytkie zrozumienie podziału i aby mogli przejść do trudniejszych zadań rozwiązywania problemów, pogłębienie ich koncepcyjnego zrozumienia podziału jest koniecznością w 3 roku.
Narodowy Program nauczania umieszcza podział w tej samej sekcji co mnożenie w latach 3-5 i umieszcza go w sekcji zwanej „czterema operacjami” w roku 6. Części zaczerpnięte z Krajowego Programu Nauczania odnoszą się tylko do tych, które konkretnie wspominają o podziale. Pozostałe elementy tych sekcji można znaleźć na blogu na temat mnożenia lub dodawania i odejmowania w stosownych przypadkach.
Czym Jest Division?
podział jest jedną z czterech operacji – czterech podstawowych pojęć matematycznych, które uczniowie powinni znać-obok dodawania i odejmowania oraz mnożenia.
gdzie mnożenie jest wielokrotnym połączeniem jednej liczby, dzielenie jest odwrotne: obliczanie, ile razy jedna liczba jest zawarta w innej. Na przykład dzielenie 10 przez 2 to pytanie, ile razy 2 mieści się w granicach 10.

z internetowych interwencji matematycznych Third Space Learning.
podział dydaktyczny KS2-teoria
podział jest odwrotnością mnożenia. Podobnie jak w przypadku bloga mnożenia, nauczanie podziału zawiera trzy podstawowe struktury, które w połączeniu z faktami podziału i zrozumieniem pojęciowym dadzą uczniom najlepszą okazję do osiągnięcia sukcesu w rozwiązywaniu problemów związanych z podziałem.
te trzy struktury współdzielą, grupują i skalują. Chociaż nie ma wystarczająco dużo czasu, aby je dogłębnie zbadać, to co poniżej będzie tylko krótkim wprowadzeniem do nich.
dzielenie i grupowanie to odwrotność mnożenia jako wielokrotnego dodawania. Współdzielenie jest koncepcją strukturalną wprowadzoną w KS1 i wcześniejszych, gdzie, jak sama nazwa wskazuje, ilość jest dzielona na równe grupy.
na przykład 12 jabłek dzieli się między 3 uczniów. Ile jabłek dostaje każdy uczeń? Tutaj znamy całą kwotę (12 jabłek) i co najważniejsze, wiemy, w jaki sposób podzielimy się kwotą (3). W zależności od tego, gdzie uczniowie są na swojej matematycznej podróży, mogą wielokrotnie odejmować o pewną liczbę (1, 2, 3 lub 4) od kwoty na trzy stosy, które reprezentują trzech uczniów.
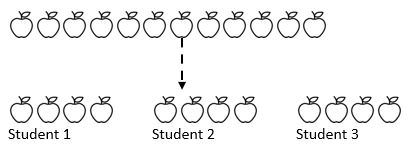
jak widać z powyższego, cała kwota została podzielona na trzy równe grupy.
grupowanie jest podobne do udostępniania, ale to, co wiemy, jest nieco inne w porównaniu do udostępniania. W strukturze współdzielenia wiemy, ile grup będzie miało miejsce współdzielenie. W strukturze grupowania znamy ilość w każdej grupie, ale nie liczbę rzeczywistych grup, które istnieją.
na przykład 12 jabłek dzieli się na grupy po 4. Ile będzie grup? Chociaż to pytanie jest bardzo podobne do powyższego, teraz przyjmuje strukturę grupowania, ponieważ wiemy, ile osób trafi do każdej grupy, ale nie wiemy już, ile grup będzie teraz.
jak wiemy, że są 4 w każdej grupie, możemy grupować 4 jabłka, dopóki nie pokryjemy wszystkich 12, aby zobaczyć, że są 3 grupy.
ostateczna struktura podziału jest skalowana. Podczas gdy w mnożeniu skalowaliśmy wartość w górę, struktura podziału skaluje się w dół. Na przykład, Shannen ma 6 długopisów, a Jen ma 3 razy mniej. Ile długopisów ma Jen?
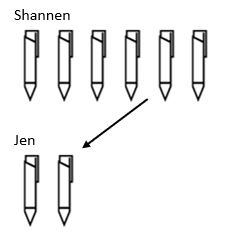
tutaj widzimy, że aby znaleźć całkowitą ilość długopisów, które ma Jen, musieliśmy wziąć ilość, którą miał Shannen i zmniejszyć ją o współczynnik skali 3 tak, że Jen kończy z 2 długopisami.
z doświadczenia wynika, że jest to najtrudniejsza struktura podziału dla uczniów do zrozumienia i zrozumienia i jest taka, którą należy ponownie przeanalizować w połączeniu ze skalowaniem jako mnożeniem, ponieważ jest to kluczowa umiejętność przy przeliczaniu pomiarów i walut z większej kwoty na mniejszą. Np. kilometry do Mil.
podział Rok 3
w National Curriculum for maths w Anglii, dla każdego obszaru matematyki nakreślonego, istnieje zarówno element ustawowy, jak i pozaregulaminowy. Element ustawowy jest następujący:
- Przypomnij i wykorzystaj fakty mnożenia i dzielenia dla tablic mnożenia 3, 4 i 8
- napisz i Oblicz matematyczne stwierdzenia mnożenia i dzielenia za pomocą znanych im tablic mnożenia, w tym dla liczb dwucyfrowych razy liczb jednocyfrowych, używając mentalnych i przechodząc do formalnych metod pisanych
- Rozwiązuj problemy, w tym problemy z brakami liczb, obejmujące mnożenie i dzielenie, w tym dodatnie problemy skalowania liczby całkowitej i problemy z korespondencją, w których n obiektów jest połączonych z m obiektów.
:
- uczniowie rozwijają efektywne metody umysłowe, np. wykorzystujące komutatywność i asocjatywność (np., 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) oraz mnożenie i dzielenie faktów (np. przy użyciu 3 × 2 = 6, 6 ÷ 3 = 2 i 2 = 6 ÷ 3) w celu wyprowadzenia powiązanych faktów (np., 30 × 2 = 60, 60 ÷ 3 = 20 i 20 = 60 ÷ 3).
- uczniowie rozwijają niezawodne metody pisane mnożenia i dzielenia, zaczynając od obliczeń dwucyfrowych liczb przez liczby jednocyfrowe, a kończąc na formalnych pisanych metodach krótkiego mnożenia i dzielenia.
- uczniowie rozwiązują proste problemy w kontekstach, decydując, którą z czterech operacji użyć i dlaczego. Należą do nich konteksty pomiaru i skalowania (na przykład cztery razy wyższe, osiem razy dłuższe itp.) i problemy z korespondencją, w których M obiekty są połączone z N obiektami (na przykład 3 kapelusze i 4 Płaszcze, ile różnych strojów?; 12 słodyczy dzielonych równo między 4 dzieci; 4 ciastka dzielone równo między 8 dzieci).
dziaĹ 'alnoĹ” Ä ‡ podziaĹ 'u Rok 3
nie obejmie to lekcji jako takiej, ale dostarczy przewodnika, jak moĹźna uczyÄ ‡ podziaĹ’ u z pewnym pojÄ ™ ciowym zrozumieniem na tym etapie. Warunkiem wstępnym byłoby nauczanie powiązanych faktów mnożenia najpierw przed nauczaniem jakiegokolwiek powiązanego podziału.
myśląc o strukturach, najlepiej w tej części nauki uczniów trzymać się grupowania i dzielenia się. W poniższych przykładach przyjrzymy się rozwijaniu przez uczniów zrozumienia dzielenia przez 4. Będzie podążać za podejściem konkretno-obrazowo-abstrakcyjnym.
często zrozumienie liczby uczniów może ograniczyć ich postępy w podziale. Szczególnie, jeśli chodzi o grupowanie i dzielenie się, gdy w sposób ciągły odbierają tylko jeden z całości.
od początku nauczania nauczyciele powinni opierać się na tym, co uczniowie już wiedzą o liczbach parzystych i innych faktach liczbowych, aby rozwinąć uczniów w liczenie w dowolnej liczbie.
liczniki mogą być używane do wykazania powiązanych faktów podziału, ponieważ uczniowie będą wykorzystywali tezy podczas budowania ich koncepcyjnego zrozumienia mnożenia. Pytania takie jak: „Ile jest grup po 4? i ile ich jest w każdej grupie?”powinny być zadawane, A odpowiedzi powinny odnosić się do tego, jak to pokazuje podział.
nauczyciel: ile jest liczników?
Dziecko: Czworo
Nauczyciel: Dobry. To jest grupa czterech osób. Ile jest grup po cztery?
Dziecko: Jedno
Nauczyciel: Doskonały. Mamy cztery liczniki w jednej grupie. Zgrupowaliśmy cztery liczniki w jedną grupę. Co my zrobiliśmy?
dziecko: zgrupowane cztery liczniki w jedną grupę.
Nauczyciel: Genialny. Kiedy grupujemy cztery liczniki w jedną grupę, wykonujemy matematyczne obliczenia czterech podzielonych przez jeden. Jakie obliczenia zrobiliśmy?
dziecko: cztery podzielone przez jeden.
nauczyciel: a kiedy rozwiążemy cztery podzielone przez jeden, odpowiedź wynosi cztery, ponieważ stworzyliśmy jedną grupę, która ma cztery elementy. Cztery podzielone przez jeden to cztery. Ile jest cztery podzielone przez jeden?
dziecko: Cztery podzielone przez jeden to cztery.
nauczyciel: doskonały
możesz zobaczyć, jak to się powtórzy w następujących przypadkach:
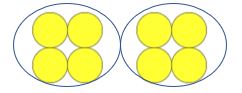
nauczyciel: ile jest liczników?
dziecko: osiem
nauczyciel: dobrze, to jest grupa czterech. Ile jest grup po cztery?
Dziecko: Dwoje
Nauczyciel: Doskonały. Mamy cztery liczniki w jednej grupie. Zgrupowaliśmy cztery liczniki w dwie grupy. Co my zrobiliśmy?
dziecko: zgrupowane cztery liczniki w dwie grupy.
Nauczyciel: Genialny. Kiedy grupujemy cztery liczniki na dwie grupy, wykonaliśmy matematyczne obliczenia ośmiu podzielonych przez dwa. Jakie obliczenia zrobiliśmy?
dziecko: osiem dzielone przez dwa.
nauczyciel: a kiedy rozwiążemy osiem podzielone przez dwa, odpowiedź wynosi cztery, ponieważ stworzyliśmy dwie grupy, które mają cztery elementy. Osiem podzielone przez dwa równa się cztery. Ile jest osiem podzielone przez dwa?
dziecko: osiem dzielone przez dwa to cztery.
nauczyciel: doskonały
kiedy uczniowie zaczynają być pewni tego, możemy przejść do innych modeli, takich jak wędki Cuisenaire.

tutaj cała kwota jest reprezentowana w górnym pociągu, a fioletowy pręt (który w tym przypadku reprezentuje 4, a jeśli czytałeś inne blogi z tej serii, mam nadzieję, że będziesz wiedział, ile jestem adwokatem za ich użycie w klasie, a więc uczniowie będą świadomi jego wartości do tego czasu) jest używany do pokazania, ile grup 4 może wejść w całkowitą kwotę.
uczniowie mogą następnie przejść do rysowania scenariuszy czytanych przez nauczyciela. Na przykład. Są 24 przyciski i muszą być pogrupowane w 4. Ile jest grup? Uczniowie mogli narysować te przyciski i pogrupować je w 4 itd.
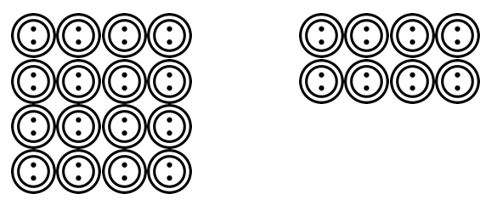
gdy uczniowie przyzwyczają się do wizualizacji scenariuszy grupowania lub dzielenia podziałów w różnych kontekstach, mogą przejść do bardziej abstrakcyjnych reprezentacji za pomocą symboli matematycznych.

3 arkusze z długim podziałem dla lat 3-6
przygotuj uczniów do długiego podziału w KS2 dzięki tym arkuszom z długim podziałem.
problemy ze słowem w podziale Rok 3
problemy ze słowem w roku 3 będą powszechnie korzystać ze struktury grupowania lub udostępniania.
jest 40 uczniów i 10 uczniów. Ile ciastek dostanie każdy uczeń?
ponieważ wiemy, ile jest grup (10), musimy obliczyć ilość na Grupę, więc jest to struktura dzielenia. Od uczniów oczekuje się, że wykorzystają swoją wiedzę na temat tabeli 4 razy, aby to wypracować i uzyskać odpowiedź 4.
podział: Rozumowanie i rozwiązywanie problemów Rok 3
w przypadku rozumowania i rozwiązywania problemów dobrym zajęciem jest dopasowanie słowa problem do obliczeń. Na przykład:
Dopasuj problemy słowne, które są rozwiązywane przez poznanie 20 podzielone przez 4.
- jest 20 ołówków i zostaną one umieszczone w paczkach po 5. Ile w każdej paczce?
- było 20 ołówków, a potem student przyniósł 4 kolejne. Ile jest teraz ołówków?
- jest 20 ołówków i zostaną one umieszczone w opakowaniach po 4. Ile w każdej paczce?
- było 20 ołówków, a potem zaginęły 4. Ile jest teraz ołówków?
zachęcanie uczniów do zapisywania wyjaśnień dla każdego pytania jest przydatne, ponieważ pozwala zobaczyć ich myślenie. Pytania zostały starannie dobrane, tak aby liczby w każdym pytaniu odnosiły się do liczb na pytaniu, więc uczniowie polegają na swoich umiejętnościach matematycznych, aby wydedukować poprawną odpowiedź.
podział rok 4
w National Curriculum for maths w Anglii, dla każdego obszaru matematyki nakreślonego, istnieje zarówno element ustawowy, jak i pozaregulaminowy. Element ustawowy jest następujący:
- Przypomnij fakty mnożenia i dzielenia dla tablic mnożenia do 12 × 12
- Użyj wartości miejsca, znanych i pochodnych faktów, aby mnożyć i dzielić mentalnie, w tym: mnożenie przez 0 i 1; dzielenie przez 1; mnożenie razem trzech liczb
:
- uczniowie nadal ćwiczą przypominanie i używanie tablic mnożenia i powiązanych faktów podziału, aby ułatwić biegłość.
- uczniowie ćwiczą metody umysłowe i rozszerzają je na trzycyfrowe liczby, aby uzyskać fakty (na przykład 600 ÷ 3 = 200 można uzyskać z 2 x 3 = 6).
- uczniowie ćwiczą biegle w formalnej pisemnej metodzie krótkiego mnożenia i krótkiego dzielenia z dokładnymi odpowiedziami
- uczniowie rozwiązują dwuetapowe problemy w kontekstach, wybierając odpowiednią operację, pracując z coraz trudniejszymi liczbami. Powinno to obejmować pytania korespondencyjne, takie jak liczba wyborów posiłku w menu lub trzy ciasta dzielone równo między 10 dzieci.
pomysły na lekcję podziału rok 4
na tej lekcji przyjrzę się, jak możesz zacząć uczyć krótkiego podziału za pomocą manipulatorów.
powiedzmy, że będziemy uczyć uczniów krótkiego podziału na pytanie 168 podzielone przez 12.
Zwykle piszemy to w tym, co jest powszechnie nazywane przystankiem autobusowym. Ale co ciekawe, różne miejsca na świecie piszą to inaczej.
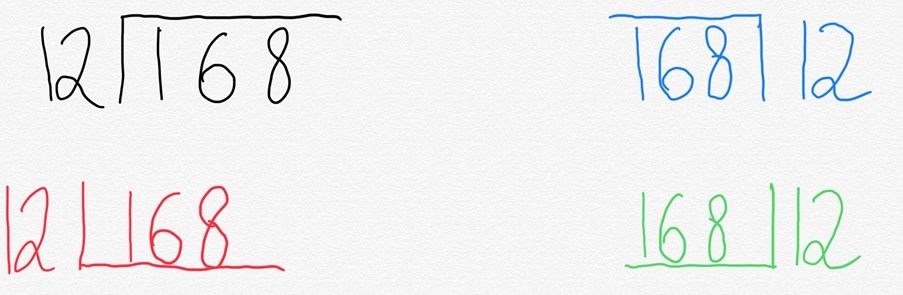
powód tego jest dość prosty. To, co właściwie reprezentuje „przystanek autobusowy”, to skrócony sposób reprezentowania prostokąta.
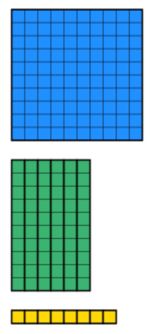
kiedy uczymy formalnego krótkiego podziału, skutecznie mówimy, że trzeba sobie wyobrazić prostokąt, w którym szerokość wynosi 12. Całkowita powierzchnia prostokąta wynosi 168 i próbujemy znaleźć brakującą długość na górze. Jak to pokazać używając manipulacji? Bloki Dienes są przydatnym narzędziem do tego.
Więc musimy zebrać 168 wartości dienów przy użyciu najmniejszej ilości bloków. Jest to pokazane poniżej.
patrząc wstecz na pytanie, wiemy, że szerokość wynosi 12. Oznacza to, że musimy teraz manipulować blokami tak, aby uzyskać szerokość 12. Zauważ, że prostokąt, musi być solidny i nie może mieć brakujących części. Na przykład, poniżej nie będzie dozwolone, mimo że jest 12 jednostek idących w dół szerokości.
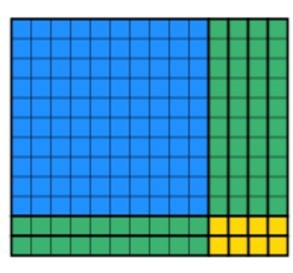
zamiast tego uczniowie mogą obrócić dwa bloki 10s, aby uzyskać następujące wyniki. Zauważ, że w każdej kolumnie jest 12 i jest to obiekt stały.
ostatnia część, którą uczniowie muszą zrobić, to użyć pozostałych bloków do stworzenia sprzedanego prostokąta przy zachowaniu szerokości 12. To może zająć trochę czasu, ale z praktyką, studenci robią szybciej. Po pewnym czasie uczniowie będą produkować to:
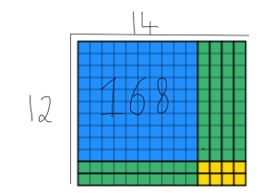
widzimy, że wszystkie 168 klocków zostało zużyte, a szerokość nadal wynosi 12. Aby znaleźć odpowiedź, uczniowie muszą policzyć długość, która w tym przypadku wynosi 14. Nałożyłem obie metody poniżej, więc możesz zobaczyć, jak się uzupełniają poniżej.
jest to przydatna strategia nauczania studentów w roku 4, ponieważ istnieją ogromne reperkusje w innych obszarach programu nauczania, które są już oświetlone dla studentów.
choć może jeszcze tego nie rozpoznają, nauczając takich krótkich podziałów już wprowadzili na obwód i obszar-pomyśl, ile czasu można zaoszczędzić na nauczaniu, gdy to połączenie zostanie nawiązane. Nie tylko to, ale w drugiej kolejności, to podejście przenosi się na myślenie algebraiczne.
problemy ze słowem w dziale rok 4
oczekuje się, że uczniowie będą czerpać ze swojej wiedzy o wartości miejsca, aby rozwiązać problemy oparte na podziale, a więc odpowiedni problem ze słowem.
w sadzie wyhodowano 4800 jabłek w sezonie. Są one umieszczane w opakowaniach po 4 przed udaniem się na rynek. Ile jest paczek?
tutaj uczniowie powinni wykorzystać fakt, że 4 x 12 = 48 i ponieważ 4800 jest sto razy więcej niż 48, 12 musi również pomnożyć przez 100, aby uzyskać 1200
podział: Rozumowanie i rozwiązywanie problemów rok 4
Czy zawsze, czasami lub nigdy prawdą jest, że suma trzech liczb parzystych jest podzielna przez 4?
to pytanie daje uczniom wiele możliwości eksperymentowania w ramach parametrów pytania. Studenci, którzy potrzebują większego wsparcia, mogą patrzeć na liczby parzyste sing digit, a uczniowie mogą przejść do wszystkiego, z czym czują się komfortowo.
przy takich otwartych pytaniach dobrze jest podać minimalne wymagania dotyczące liczby prób, które uczniowie powinni wykonać, w przeciwnym razie często zdecydują się wykonać minimum.
odpowiedź na to pytanie jest czasami.
szybki „trick”, aby dowiedzieć się, czy liczba jest podzielna, to spojrzeć na ostatnie 2 cyfry liczby i sprawdzić, czy są podzielne przez 4. Na przykład, jeśli dziecko znalazło sumę 34, 36 i 38 i dostało 108, jako nauczyciel wiem, że ta liczba jest podzielna przez 4, ponieważ ostatnie dwie cyfry (08) tworzą 8 i są podzielne przez 4. Jeśli dziecko wybrało 34, 36 i 48, aby uzyskać 118, wiem, że to nie jest podzielne przez 4, ponieważ 18 – ostatnie dwie cyfry 118 – nie są podzielne przez 4.
podział Rok 5
w National Curriculum for maths w Anglii, dla każdego obszaru matematyki nakreślonego, istnieje zarówno element ustawowy, jak i pozaregulaminowy. Element ustawowy jest następujący:
- Mnoż i dziel liczby mentalnie na podstawie znanych faktów
- dziel liczby do 4 cyfr przez jednocyfrową liczbę przy użyciu formalnej pisemnej metody krótkiego dzielenia i interpretuj pozostałości odpowiednio do kontekstu
- Mnoż i dziel liczby całkowite i te z ułamkiem dziesiętnym przez 10, 100 i 1000
- Rozwiązuj problemy związane z mnożeniem i dzieleniem, w tym wykorzystując ich znajomość czynników i wielokrotności, kwadraty i kostki
- rozwiązują problemy związane z dodawaniem, odejmowaniem, mnożeniem i dzieleniem oraz kombinacją te, w tym zrozumienie znaczenia znaku równości
- , rozwiązują problemy związane z mnożeniem i dzieleniem, w tym skalowanie przez ułamki proste i problemy związane z szybkościami prostymi.
:
- uczniowie interpretują odpowiedzi inne niż całkowite do podziału, wyrażając wyniki na różne sposoby, w zależności od kontekstu, w tym z pozostałościami, jako ułamki, jako ułamki dziesiętne lub zaokrąglając (na przykład 98 ÷ 4 = = 24 r 2 = 24 = 24,5 ≈ 25).
- uczniowie używają mnożenia i dzielenia jako odwrotności, aby wspierać wprowadzenie współczynnika w roku 6, na przykład przez mnożenie i dzielenie przez potęgi 10 w rysunkach w skali lub przez mnożenie i dzielenie przez potęgi 1000 w przeliczaniu między jednostkami, takimi jak kilometry i metry.
działalność działu Rok 5
podział w roku 5 postępuje poprzez wykorzystanie resztek w odpowiedziach. W tej lekcji przyjrzę się innym manipulatorom, których nauczyciele mogą używać do nauczania podziału 4 na 1 cyfrę.
jeśli pytanie było 5,642 podzielone przez 4, możemy przedstawić to za pomocą wykresu wartości miejsca i liczników wartości miejsca, jak widać poniżej.
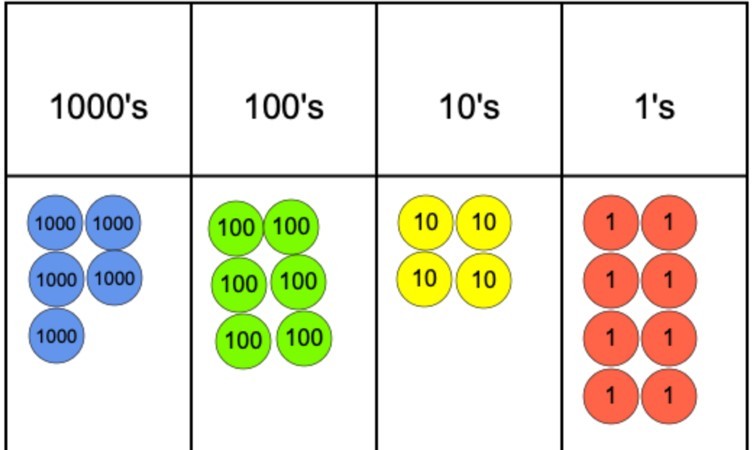
następnym krokiem byłoby pogrupowanie liczników w 4, ponieważ jest to nasz dzielnik. Jednak, jak widać, szybko dochodzimy do problemu w kolumnie 1000, ponieważ jesteśmy w stanie zgrupować 4 liczniki, ale wtedy nie możemy zgrupować pozostałego licznika w grupie 4.
aby zwalczyć ten problem, licznik 1000, który nie został zgrupowany, można wymienić na dziesięć liczników 100. Można je następnie pogrupować w grupy po 4 i może się to zdarzyć bez żadnych liczników 100s w lewo. Stamtąd jest to prosty przypadek przejścia do 10s i wreszcie te.
ponieważ istnieje dziewięć liczników 1s, możemy pogrupować 8 z nich w 2 grupy i 4 i twierdzić, że została jedna*. Aby znaleźć odpowiedź, wszystko, co jest wymagane, to policzyć liczbę grup wykonanych w każdej wartości miejsca i użyć ich do zapisu cyfr, aby utworzyć ostateczną odpowiedź. W tym przypadku odpowiedź brzmiałaby 1,412 reszta 1.
* gdy patrzysz na liczby dziesiętne, możesz wymienić pozostały licznik 1s na dziesięć liczników 0.1 i kontynuować dzielenie zgodnie z opisem powyżej. Znajomość tego modelu jest przydatna, ponieważ może pomóc w demystyfikacji podziału za pomocą miejsc dziesiętnych, z którymi uczniowie mogą się zmagać. Pomaga im to dostrzec, że jest to kontynuacja procesu, który już znają, a nie coś nowego.
problemy z podziałem Rok 5
podczas dzielenia W roku 5 uczniowie napotkają scenariusze, w których będą musieli podsumować swoją odpowiedź, aby odpowiedź miała sens w kontekście. Odpowiednie pytanie, które pokazuje, że byłoby to coś w stylu:
Szkoła planuje dyskotekę towarzyską, w której planuje zaoferować każdemu uczniowi 250 ml soku. Mogą kupić 2 litrowe butelki soku. Spodziewają się 33 uczniów, więc wiedzą, że wydadzą 8,25 litra soku. Ile butelek soku będą musieli kupić?
wspólna odpowiedź jest taka, że uczniowie powiedzą 4 i ćwiartka. Jednakże, ponieważ nie można kupić ćwierć butelki, w tym przypadku prawidłowa odpowiedź brzmiałaby 5 butelek soku, które byłyby potrzebne, aby zapewnić, że wszyscy uczniowie mogą wziąć udział.
Dział: rozumowanie i rozwiązywanie problemów Rok 5
jak wspomniano powyżej, w roku 5 uczniowie napotkają scenariusze w ramach wydziału, w których będą musieli wybrać, czy odpowiedź ma być zaokrąglona w górę, czy w dół. Na przykład, gdy pytanie zadaje uczniom pytanie, ile autobusów jest potrzebnych do szkoły na wycieczkę.
zachęcanie uczniów do tworzenia własnych problemów przy użyciu różnych kontekstów może być naprawdę trudnym działaniem, które zmusza uczniów do matematycznego myślenia o kontekście i podziale.
uczniowie mogą następnie zamienić te pytania, które stworzyli z partnerem, a następnie rozwiązać je i sprawdzić u oryginalnego twórcy pytania, czy mają poprawną odpowiedź.
podział Rok 6
w National Curriculum for maths w Anglii, dla każdego obszaru matematyki nakreślonego, istnieje zarówno element ustawowy, jak i pozaregulaminowy. Element ustawowy jest następujący:
- dziel liczby do 4 cyfr przez dwucyfrową liczbę całkowitą przy użyciu formalnej pisemnej metody długiego dzielenia i interpretuj pozostałości jako pozostałości liczb całkowitych, ułamki lub zaokrąglając, odpowiednio do kontekstu
- dziel liczby do 4 cyfr przez dwucyfrową liczbę przy użyciu formalnej pisemnej metody krótkiego dzielenia tam, gdzie to stosowne, interpretując pozostałości zgodnie z kontekstem
- wykonuj obliczenia umysłowe, w tym z operacjami mieszanymi i dużymi liczby
- określają współczynniki wspólne, wielokrotności wspólne i liczby pierwsze
- wykorzystaj swoją wiedzę o kolejności operacji do przeprowadzenia obliczeń dotyczących czterech operacji
:
- Rozwiązywanie problemów związanych z dodawaniem, odejmowaniem, mnożeniem i dzieleniem
- użyj estymacji, aby sprawdzić odpowiedzi na obliczenia i określić, w kontekście problemu, odpowiedni stopień dokładności.
pomysły na lekcję podziału Rok 6
Sophie Bartlett (@_MissieBee) stworzyła tutaj doskonały blog (link do bloga Sophie na temat nauczania długiego podziału) opisujący, w jaki sposób uczyłaby długiego podziału przez klasę 6 roku. Ponieważ long division jest jedyną nową nauką na temat podziału w szóstym roku, jest to idealny sposób na wprowadzenie procedury długiego podziału.
pytania o podział Rok 6
typowy problem ze słowem podziałowym, z którym zetknie się uczeń 6 roku to:
Szkoła zebrała 3146 zł ze sprzedaży wypieków. W wydarzeniu wzięło udział 104 rodziców. Jeśli wszyscy rodzice wydali taką samą kwotę pieniędzy, ile wydali każdy rodzic?
tutaj uczniowie powinni skorzystać z metody długiego podziału, aby rozwiązać to pytanie, aby uzyskać odpowiedź 30,25 zł.
Dział: rozumowanie i rozwiązywanie problemów Rok 6
przy czymś proceduralnym, takim jak długi podział, dobrym działaniem rozumowania jest nakłonienie uczniów do znalezienia błędów. Środki te zapewniają duży bank takich działań. Jak widać z poniższego pytania, uczniowie wykonali całą ciężką pracę, ale niedbały błąd w liczeniu grup 59 oznacza, że dziecko wierzyło, że 59 x 7 to 472, a nie 59 x 8.
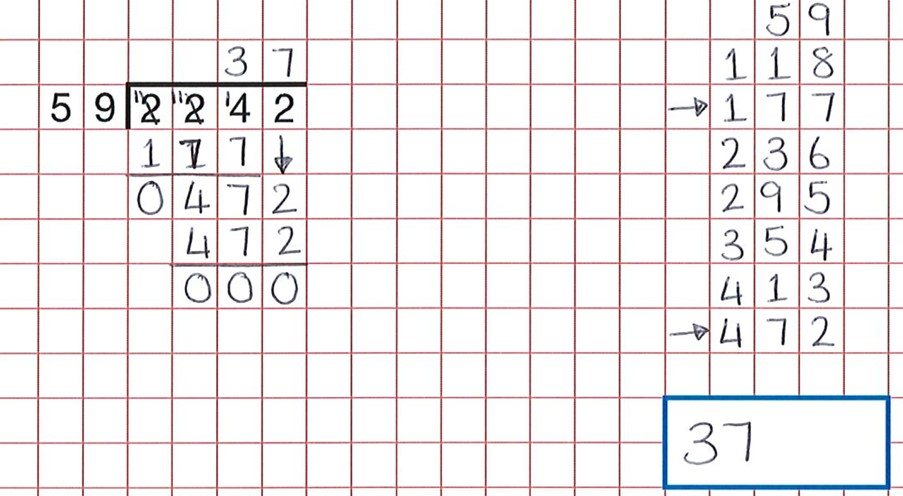
prawidłowa odpowiedź to 38.
podział to kluczowy temat matematyczny, nie tylko w KS2, ale w matematyce jako całości. Mam nadzieję, że ten post dał ci kilka dobrych pomysłów, aby pomóc uczniom podejść do niego z pewnością siebie.
online 1-to-1 lekcje matematyki zaufane przez szkoły i nauczycieli
co tydzień nauczyciele specjalizujący się w matematyce w programie Space learning wspierają tysiące dzieci w szkołach podstawowych dzięki cotygodniowym lekcjom online 1-to-1 i interwencjom matematycznym. Od 2013 roku pomogliśmy ponad 100 000 dzieci stać się bardziej pewni siebie, zdolni matematycy. Dowiedz się więcej lub poproś o spersonalizowaną wycenę, aby porozmawiać z nami o twoich potrzebach i tym, jak możemy Ci pomóc.
nauczanie w Szkole Podstawowej dostosowane do potrzeb każdego dziecka i ściśle zgodne z Krajowym programem nauczania.