w tym przewodniku wyjaśnię, czym jest formuła błędu standardowego i jak jej użyć, aby wypracować błąd Standardowy za pomocą przykładu.
co to jest błąd standardowy?
błąd standardowy (SE), czasami określany jako błąd standardowy średniej (SEM), jest statystyką odpowiadającą standardowemu odchyleniu rozkładu próbkowania w stosunku do średniej wartości. Ale co to właściwie jest?
powiedz, że jesteś zainteresowany przeciętnym wiekiem ludzi w Wielkiej Brytanii zdiagnozowano chorobę Alzheimera. Nie jest możliwe ustalenie tego dla wszystkich w Wielkiej Brytanii, dlatego naukowcy pobierają próbkę populacji, aby uogólnić ogólną liczbę. Na przykład, 10.000 Brytyjczyków z chorobą mogą być analizowane i zostaną wykorzystane do wygenerowania średniego wieku diagnozy. Jeśli zrobisz to na losowej próbie 5000 pacjentów, możesz uzyskać średni wiek diagnozy 61,5 roku. Jeśli jednak wykonasz analizę próbki na oddzielnej losowej próbie 10 000 innych pacjentów, możesz uzyskać średni wiek 62,3 lat. Załóżmy, hipotetycznie rzecz biorąc, że gdybyś był w stanie przeanalizować wszystkich ludzi w Wielkiej Brytanii, którzy mają chorobę Alzheimera, aby uzyskać rzeczywistą liczbę, możesz skończyć z 64,3 latami. Można zauważyć, że dane uzyskane z populacji próbki (61,5 i 62,3 lat) różni się do rzeczywistej liczby (64,3 lat). Ta zmienność średnich wartości jest oczekiwana, a wraz ze wzrostem liczby osób w populacji próbki otrzymasz wartość, która jest bliższa rzeczywistej wartości. Dokładnie to reprezentuje błąd standardowy. Błąd standardowy oznacza tę zmianę średnich wartości między populacjami próbki.
w celu dalszej lektury proponuję przeczytać krótką notkę statystyczną profesorów Douglasa Altmana i Martina Blanda opublikowaną w British Medical Journal. Jest to pomocny wgląd w to, czym jest błąd standardowy i jaka jest różnica z odchyleniem standardowym.
standardowa formuła błędu
aby obliczyć standardowy błąd, musisz mieć dwie informacje: odchylenie standardowe i liczbę próbek w zestawie danych. Błąd standardowy oblicza się dzieląc odchylenie standardowe przez pierwiastek kwadratowy liczby próbek.
Oto pełna formuła błędu standardowego z adnotacjami:
przykład
aby lepiej zrozumieć formułę błędu standardowego, może pomóc przejść przez przykład. Powiedzmy, że mamy populację 80 osób i jesteśmy zainteresowani ich wzrostem. Mierzymy ich wysokość i obliczamy odchylenie standardowe na 30,6 cm. Teraz musimy podłączyć te wartości do naszego równania:
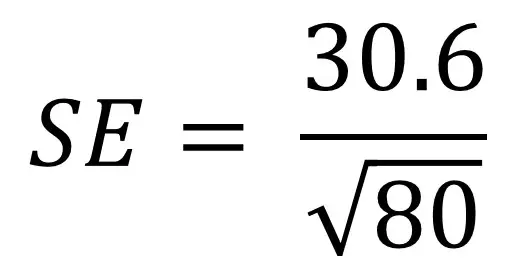 jeśli nie chcesz wprowadzać równań do kalkulatorów, możesz podzielić formułę na łatwe do opanowania fragmenty. Oto kroki, które możesz podjąć.
jeśli nie chcesz wprowadzać równań do kalkulatorów, możesz podzielić formułę na łatwe do opanowania fragmenty. Oto kroki, które możesz podjąć.
- po pierwsze, Oblicz pierwiastek kwadratowy liczby próbek (n). W tym przypadku n jest 80. Pierwiastek kwadratowy z 80 wynosi 8,94.
- następnie podziel odchylenie standardowe (30.6) przez pierwiastek kwadratowy z 80 (8.94). Daje to wartość 3,42.
- dlatego standardowy błąd w naszej populacji dla wzrostu wynosi 3,42 cm.