I denne veiledningen vil jeg forklare hva standardfeilformelen er og hvordan du bruker den til å utarbeide standardfeilen ved bruk av et eksempel.
hva er standardfeilen?
STANDARDFEILEN (SE), noen ganger referert til som standardfeilen til gjennomsnittet (SEM), er en statistikk som tilsvarer standardavviket til en utvalgsfordeling, i forhold til middelverdien. Men hva er det egentlig?
Si at du er interessert i gjennomsnittsalderen folk i STORBRITANNIA er diagnostisert Med Alzheimers sykdom. Det er ikke mulig å bestemme dette for ALLE I STORBRITANNIA, derfor tar forskerne en utvalgspopulasjon for å generalisere en samlet figur. For eksempel kan 10.000 Britiske personer med sykdommen bli analysert og vil bli brukt til å generere gjennomsnittsalderen for diagnose. Hvis du gjør dette på et tilfeldig utvalg av 5000 pasienter, kan du få en gjennomsnittsalder på diagnose på 61,5 år. Men hvis du gjør prøveanalysen på en separat tilfeldig prøve på 10 000 andre pasienter, kan du få en gjennomsnittsalder på 62,3 år. La oss si, hypotetisk sett selvfølgelig, at hvis du var i stand til å analysere alle menneskene I STORBRITANNIA som har Alzheimers sykdom for å få den faktiske figuren, kan du ende opp med 64,3 år. Du kan legge merke til at tallene fra utvalgspopulasjonene (61,5 og 62,3 år) skiller seg fra det faktiske tallet (64,3 år). Denne variasjonen i middelverdier forventes, og når du øker antall personer i utvalgspopulasjonen, får du en verdi som er nærmere det faktiske tallet. Dette er akkurat hva standardfeilen representerer. Standardfeilen betyr denne variasjonen i middelverdiene mellom utvalgspopulasjonene.
for videre lesing foreslår jeg at du leser den korte Statistikknotatet Av Professorene Douglas Altman og Martin Bland publisert i British Medical Journal. Det er et nyttig innblikk i hva standardfeilen er og hva forskjellen med standardavviket.
standardfeilformelen
for å beregne standardfeilen må du ha to opplysninger: standardavviket og antall prøver i datasettet. Standardfeilen beregnes ved å dele standardavviket med kvadratroten av antall prøver.
Her er den fulle annoterte standardfeilformelen:
Eksempel
for å forstå standardfeilformelen bedre, kan det hjelpe å gå gjennom et eksempel. Si at vi har en befolkning på 80 personer, og vi er interessert i deres høyde. Vi måler høyden og beregner standardavviket som 30,6 cm. Vi må nå koble disse verdiene til vår ligning:
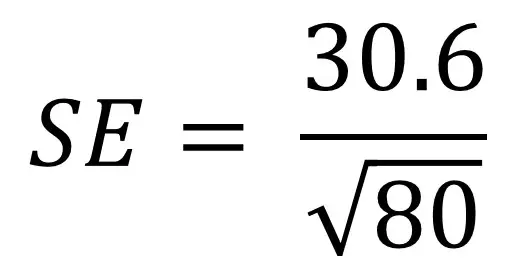hvis du er ubehagelig med å legge inn ligninger i kalkulatorer, kan du bryte ned formelen i håndterbare biter. Her er trinnene du kan ta.
- beregn først kvadratroten av antall prøver (n). I dette tilfellet er n 80. Kvadratroten på 80 er 8,94.
- del deretter standardavviket (30,6) med kvadratroten på 80 (8,94). Å gjøre dette gir en verdi på 3,42.
- derfor er standardfeilen i vår befolkning for høyde 3,42 cm.