Divisjon I Nøkkelfase 2 danner den siste delen av De Fire Operasjonene – de fire kjernematiske konseptene elevene bør vite. Denne bloggen vil hjelpe deg med å sikre at alle elevene dine, fra År 3 Til År 6, kan nærme seg divisjon med den tilliten de trenger for å lykkes.
Divisjon I ks2 matematikk bygger på det som har blitt lært PÅ KS1. Ved slutten Av Y2 studenter på forventet standard vil være i stand til å ‘ huske og bruke multiplikasjon og divisjon fakta for 2, 5 og 10 gangetabellen, inkludert gjenkjenne oddetall og partall.’
for lærere I År 3 er det alltid en god ide å sikre at elevene kjenner disse veldig bra. Med det mener jeg ikke bare at de kan papegøye divisjonsfakta på deg, men de forstår virkelig hvordan de skal representere disse fakta både med konkrete representasjoner, verbale forklaringer og gjennom andre billedlige metoder.
Studenter som ikke er i stand til å gjøre dette, men er i stand til verbalt å fortelle deg divisjonsfakta, har en veldig grunne forståelse av divisjon og for at de skal kunne gå videre til vanskeligere problemløsende aktiviteter, utdype deres konseptuelle forståelse av divisjon er et must i År 3.
Den Nasjonale Læreplanen plasserer divisjon innenfor samme seksjon som multiplikasjon I År 3-5 og plasserer den innenfor en seksjon kalt ‘Fire Operasjoner’ I År 6. Delene tatt fra Den Nasjonale Læreplanen gjelder bare de som spesifikt nevner divisjon. De andre elementene i disse seksjonene kan bli funnet i bloggen på multiplikasjon eller addisjon og subtraksjon der det er hensiktsmessig.
Hva Er Divisjon?
Divisjon er en Av De Fire Operasjonene-de fire sentrale matematiske konseptene elevene bør vite-sammen med addisjon og subtraksjon og multiplikasjon.
hvor multiplikasjon kombinerer ett tall flere ganger, er divisjon motsatt: å regne ut hvor mange ganger et tall er inneholdt i en annen. For eksempel, å dele 10 med 2 spør hvor mange ganger 2 er inneholdt i 10.

fra Third Space Learning ‘ s online maths interventions.
Teaching Division KS2-Teorien
Divisjon Er den inverse av multiplikasjon. Som med multiplikasjonsbloggen inneholder undervisningen i divisjon tre underliggende strukturer, som, når de kombineres med divisjonsfakta og konseptuell forståelse, vil gi studentene den beste muligheten til å lykkes når de løser problemer knyttet til divisjon.
de tre strukturene deler, grupperer og skalerer. Selv om det ikke er nok tid til å utforske disse i dybden, vil det følgende bare være en kort introduksjon til dem.
Deling og gruppering er den inverse av multiplikasjon som gjentatt tillegg. Deling er et strukturelt konsept som innføres I KS1 og tidligere der, som navnet antyder, et beløp deles i like grupper.
for eksempel deles 12 epler blant 3 studenter. Hvor mange epler får hver elev? Her vet vi hele beløpet (12 epler)og avgjørende, vi vet hvordan beløpet vi skal dele inn (3). Avhengig av hvor elevene er på sin matematiske reise, kan de gjentatte ganger trekke av noen tall (1, 2, 3 eller 4) fra mengden i tre hauger som representerer de tre studentene.
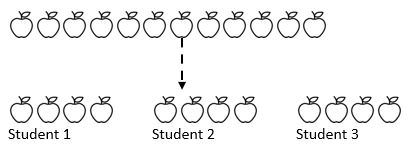
Som vi kan se fra ovenstående, har hele beløpet blitt delt inn i tre like grupper.
Gruppering ligner på deling, men Det vi vet er litt annerledes i forhold til deling. I delingsstrukturen vet vi hvor mange grupper som delingen vil finne sted. I gruppestrukturen vet vi beløpet i hver gruppe, men ikke antall faktiske grupper som det er.
for eksempel deles 12 epler i grupper på 4. Hvor mange grupper vil det være? Selv om dette spørsmålet er svært lik den ovenfor, det tar nå på gruppestrukturen som vi vet hvor mange vil gå inn i hver gruppe, men ikke lenger vet hvor mange grupper det vil nå være.
Som vi vet at det er 4 i hver gruppe, kan vi gruppere 4 epler til vi har dekket alle 12 for å se at det er 3 grupper.
den endelige strukturen i divisjonen er skalering. Mens vi i multiplikasjon skalerer opp en verdi, skalerer divisjonsstrukturen ned. For Eksempel Har Shannen 6 penner og Jen har 3 ganger så færre. Hvor mange penner Har Jen?
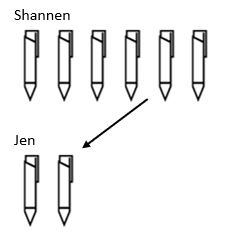
her kan vi se at for å finne den totale mengden penner Som Jen har, måtte vi ta beløpet Som Shannen hadde og redusere det med en skalafaktor på 3 slik At Jen ender opp med 2 penner.
fra erfaring er dette den vanskeligste divisjonsstrukturen for elevene å forstå og forstå, og er en som må revideres i forbindelse med skalering som multiplikasjon, da dette er en viktig ferdighet når man konverterer målinger og valutaer fra et større beløp til et mindre beløp. F. Eks. Kilometer til miles.
Divisjon År 3
I Den Nasjonale Læreplanen for matematikk I England, for hvert område av matematikk skissert, er det både en lovfestet element og en ikke-lovfestet element. Det lovbestemte elementet er som følger:
- Tilbakekall og bruk multiplikasjon og divisjon fakta for 3, 4 og 8 gangetabellen
- Skriv og beregne matematiske setninger for multiplikasjon og divisjon ved hjelp av gangetabellen som de vet, inkludert for tosifrede tall ganger ettsifrede tall, ved hjelp av mentale og utvikler seg til formelle skriftlige metoder
- Løse problemer, inkludert manglende tall problemer, involverer multiplikasjon og divisjon, inkludert positive heltall skalering problemer og korrespondanse problemer der n objekter er koblet til m objekter.
ikke-lovbestemte notater og veiledning:
- Elevene utvikler effektive mentale metoder, for eksempel ved hjelp av kommutativitet og assosiativitet (for eksempel, 4 × 12 × 5 = 4 × 5 × 12 = 20 × 12 = 240) og multiplikasjon og divisjon fakta (for eksempel ved hjelp av 3 × 2 = 6, 6 ÷ 3 = 2 og 2 = 6 ÷ 3) for å utlede relaterte fakta (for eksempel, 30 × 2 = 60, 60 ÷ 3 = 20 og 20 = 60 ÷ 3).
- Elevene utvikler pålitelige skriftlige metoder for multiplikasjon og divisjon, som starter med beregninger av tosifrede tall med ensifrede tall og går videre til formelle skriftlige metoder for kort multiplikasjon og divisjon.
- Elevene løser enkle problemer i sammenhenger, bestemmer hvilken av de fire operasjonene Som skal brukes og hvorfor. Disse inkluderer måling og skalering sammenhenger, (for eksempel fire ganger så høy, åtte ganger så lang etc.) og korrespondanse problemer der m objekter er koblet til n objekter (for eksempel 3 hatter og 4 strøk, hvor mange forskjellige antrekk?; 12 søtsaker deles likt mellom 4 barn, 4 kaker deles likt mellom 8 barn).
Divisjonsaktiviteter År 3
Dette vil ikke dekke en leksjon i seg selv, Men gi en veiledning om hvordan divisjon kan undervises med litt konseptuell forståelse på dette stadiet. En forutsetning for dette ville være undervisning av relaterte multiplikasjon fakta først før undervisning noen relatert divisjon.
når du tenker på strukturer, er det best på denne delen av studenters læringsreise å holde fast ved gruppering og deling. For de følgende eksemplene vil vi se på å utvikle elevers forståelse for å dele med 4. Det vil følge Den Konkrete-Billedlige-Abstrakte tilnærmingen.
det er ofte elevenes forståelse av tall som kan begrense deres fremgang i divisjon. Spesielt når det gjelder gruppering og deling når de bare tar en bort kontinuerlig fra hele.
fra begynnelsen av undervisningsavdelingen bør lærerne lene seg på hva elevene allerede vet om like tall og andre tallfakta for å utvikle elevene til å telle i det nummeret som kan være hensiktsmessig.
Tellere kan brukes til å demonstrere relaterte divisjon fakta som studenter vil ha brukt teser når bygge sin konseptuelle forståelse av multiplikasjon. Spørsmål som, ‘hvor mange grupper på 4 er det? hvor mange er det i hver gruppe?- det skal stilles spørsmål og svarene skal forholde seg til hvordan dette viser splittelse.
Lærer: Hvor mange tellere er det?
Barn: Fire
Lærer: Bra. Dette er en gruppe på fire. Hvor mange grupper på fire er det?
Barn:En
Lærer: Utmerket. Vi har fire tellere i en gruppe. Vi har gruppert fire tellere i en gruppe. Hva har vi gjort?
Barn: Gruppert fire tellere i en gruppe.
Lærer: Strålende. Når vi grupperer fire tellere i en gruppe, har vi gjort den matematiske beregningen av fire delt med en. Hvilken beregning har vi gjort?
Barn: Fire delt på en.
Lærer: og når vi løser fire delt på en, er svaret fire fordi vi har laget en gruppe som har fire elementer i den. Fire delt på en er fire. Hva er fire delt på en?
Barn: Fire delt på en er fire.
Lærer: Utmerket
Du kan se hvordan det ville bli gjentatt for følgende:
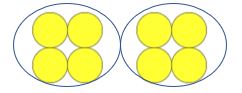
Lærer: Hvor mange tellere er det?
Barn: Åtte
Lærer: Bra, dette er en gruppe på fire. Hvor mange grupper på fire er det?
Barn:To
Lærer: Utmerket. Vi har fire tellere i en gruppe. Vi har gruppert fire tellere i to grupper. Hva har vi gjort?
Barn: Gruppert fire tellere i to grupper.
Lærer: Strålende. Når vi grupperer fire tellere i to grupper, har vi gjort den matematiske beregningen av åtte delt på to. Hvilken beregning har vi gjort?
Barn: Åtte delt på to.
Lærer: og når vi løser åtte delt på to, er svaret fire fordi vi har laget to grupper som har fire elementer i den. Åtte delt på to er fire. Hva er åtte delt på to?
Barn: Åtte delt på to er fire.
Lærer: Utmerket
når elevene begynner å bli trygg med dette, kan vi gå videre til andre modeller som Cuisenaire stenger.

her hele beløpet er representert i toppen tog og lilla stang (som i dette tilfellet representerer 4 og hvis du har lest andre blogger i denne serien forhåpentligvis vil du vite hvor mye av en advokat jeg er for deres bruk i klasserommet og så elevene vil være klar over sin verdi da) brukes til å vise hvor mange grupper på 4 kan gå inn i det totale beløpet.
Elevene kan deretter gå videre til å tegne scenarier lest av læreren. Eksempelvis. Det er 24 knapper og de må grupperes i 4. Hvor mange grupper er det? Studentene kan tegne disse knappene og gruppere dem inn i 4 etc.
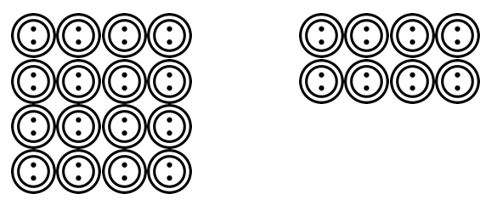
når elevene har blitt vant til å kunne visualisere disse grupperings-eller delingsdivisjonsscenariene i en rekke sammenhenger, kan de gå videre til mer abstrakte representasjoner ved hjelp av matematiske symboler.

3 Long Division Regneark For År 3-6
Få elevene prepped for lang divisjon GJENNOM KS2 med disse long division regneark.
Divisjon Tekstproblemer År 3
Tekstproblemer I År 3 vil vanligvis bruke gruppering eller deling struktur.
Det er 40 kaker og 10 studenter. Hvor mange kaker ville hver elev få?
Siden vi vet hvor mange grupper det er (10) må vi regne ut beløpet per gruppe, så dette er en delingsstruktur. Studentene forventes å bruke sin kunnskap om 4 times table for å finne ut av dette og få svaret 4.
Divisjon: Resonnement Og Problemløsning År 3
for resonnement og problemløsning, en god aktivitet jeg finner er å matche et ord problem til en beregning. For eksempel:
Match ordet problemer som er løst ved å vite 20 dividert med 4.
- det er 20 blyanter og de skal plasseres i pakker med 5. Hvor mange i hver pakke?
- det var 20 blyanter og deretter en student bringer i 4 mer. Hvor mange blyanter er det nå?
- det er 20 blyanter og de skal plasseres i pakker med 4. Hvor mange i hver pakke?
- det var 20 blyanter og deretter 4 forsvinner. Hvor mange blyanter er det nå?
Å få elevene til å skrive ned sine forklaringer for hvert spørsmål er nyttig som det gjør det mulig å se deres tenkning. Spørsmålene er valgt nøye slik at tallene i hvert spørsmål er knyttet til tallene på spørsmålet, slik at elevene stoler på deres matematiske ferdigheter for å utlede det riktige svaret.
Divisjon År 4
I Den Nasjonale Læreplanen for matematikk I England, for hvert område av matematikk skissert, er det både en lovfestet element og en ikke-lovfestet element. Det lovbestemte elementet er som følger:
- Recall multiplikasjon og divisjon fakta for gangetabellen opp til 12 × 12
- Bruk sted verdi, kjente og avledede fakta å multiplisere og dividere mentalt, inkludert: multiplisere med 0 og 1; dividere med 1; multiplisere sammen tre tall
Ikke-lovbestemte notater og veiledning:
- Elevene fortsetter å øve på å huske og bruke multiplikasjonstabeller og relaterte divisjonsfakta for å hjelpe flyt.
- Elever praktiserer mentale metoder og utvider dette til tresifrede tall for å utlede fakta, (for eksempel kan 600 ÷ 3 = 200 utledes fra 2 x 3 = 6).
- Elevene øver seg på å bli flytende i den formelle skriftlige metoden for kort multiplikasjon og kort divisjon med eksakte svar
- Elevene løser to-trinns problemer i sammenhenger, velger riktig operasjon, arbeider med stadig vanskeligere tall. Dette bør inkludere korrespondanse spørsmål som antall valg av et måltid på en meny, eller tre kaker deles likt mellom 10 barn.
Divisjonsleksjonsideer År 4
for denne leksjonen vil jeg se på hvordan du kan begynne å lære kort divisjon ved hjelp av manipulativer ved siden av den.
Si at vi skal lære elevene kort divisjon for spørsmålet 168 dividert med 12.
vi vil normalt skrive dette i det som ofte refereres til som busstopp. Men det som er interessant er at forskjellige steder i verden skriver det annerledes.
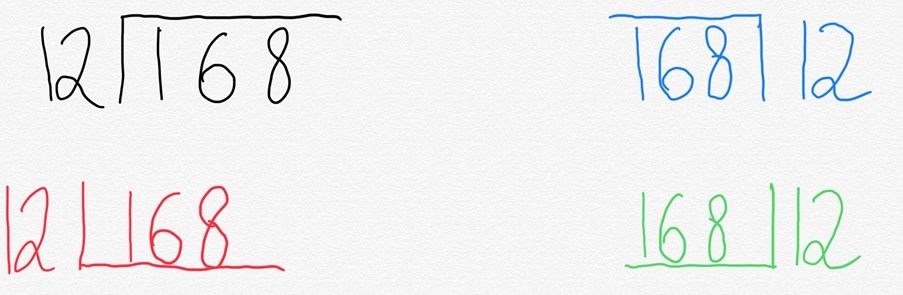
årsaken til dette er ganske enkelt. Hva bussholdeplassen egentlig representerer, er en forkortet måte å representere et rektangel på.
når vi lærer formell kort divisjon, er det vi effektivt sier at du må forestille deg et rektangel hvor bredden er 12. Det totale arealet av rektangelet er 168 og vi forsøker å finne den manglende lengden over toppen. Så hvordan viser vi dette ved hjelp av manipulativer? Dienes blokker er et nyttig verktoy for dette.
vi vet at totalbeløpet er 168. Så vi trenger å samle 168 verdt av diener ved hjelp av de minste mengder blokker mulig. Dette er vist nedenfor.
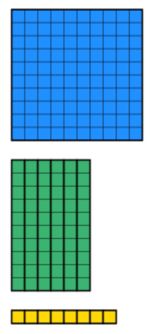
Når vi Ser tilbake på spørsmålet, vet vi at bredden er 12. Det betyr at vi nå må manipulere blokkene slik at vi får en bredde på 12. Merk at rektangelet, må være solid og kan ikke ha noen manglende deler. For eksempel, nedenfor ville ikke være tillatt til tross for at det er 12 enheter går ned bredden.
i Stedet kan elevene rotere to 10s blokker for å få følgende. Legg merke til hvordan det er 12 i hver kolonne og det er et solidt objekt.
den siste delen studentene må gjøre, er å bruke de resterende blokkene til å lage et solgt rektangel mens bredden holdes 12. Dette kan ta litt tid, men med praksis, elevene får raskere. Etter en tid vil studentene produsere dette:
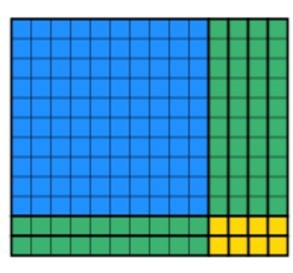
Vi kan se at alle 168 verdt av blokker har blitt brukt opp og at bredden er fortsatt 12. For å finne svaret, må studentene telle lengden, som i dette tilfellet er 14. Jeg har lagt begge metodene nedenfor, slik at du kan se hvordan de utfyller hverandre nedenfor.
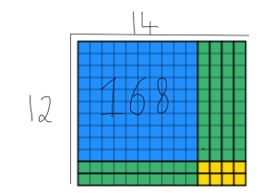
Dette er en nyttig strategi for å undervise studenter i År 4, da det er massive konsekvenser i andre områder av læreplanen som allerede er opplyst for studenter.
selv om de kanskje ikke gjenkjenner det ennå, har de allerede blitt introdusert til perimeter og område ved å undervise i kort divisjon som dette – tenk hvor mye undervisningstid som kan lagres når denne forbindelsen er gjort. Ikke bare det, men i sekundær overfører denne tilnærmingen til algebraisk tenkning.
Divisjon Ord Problemer År 4
Studenter vil bli forventet å trekke på sin kunnskap om sted verdi for å løse divisjonsbaserte problemer og så en passende ord problem ville være.
en frukthage dyrket 4800 epler i en sesong. De er plassert i pakker på 4 før de går til markedet. Hvor mange pakker er det?
her skal studentene bruke det faktum at 4 x 12 = 48 og som 4800 er hundre ganger mer enn 48, 12 må også multipliseres med 100 for å få 1200
Divisjon: Begrunnelse Og Problemløsning År 4
Er det alltid, noen ganger eller aldri sant at summen av tre like tall er delelig med 4?
Dette spørsmålet gir studentene rikelig med mulighet til å eksperimentere innenfor parametrene til spørsmålet. Studenter som trenger mer støtte kan se på sing siffer partall og studenter kan gå opp til hva de føler seg komfortabel med.
med åpne spørsmål som dette, er det godt å gi et minimumskrav for hvor mange forsøk studentene skal gjøre ellers vil de ofte velge å gjøre det minste minimum.
svaret på dette spørsmålet er noen ganger.
et raskt ‘triks’ for å vite om et tall er delbart, er å se på de siste 2 sifrene i nummeret og se om de er delbare med 4. For eksempel, hvis et barn fant summen av 34, 36 og 38 og fikk 108, vet jeg som lærer at dette tallet er delbart med 4 som de to siste sifrene (08) gjør 8 og er delbare med 4. Hvis et barn valgte 34, 36 og 48 for å få 118, vet jeg at dette ikke er delbart med 4 da 18-de to siste sifrene i 118 – ikke er delbare med 4.
Divisjon År 5
I Den Nasjonale Læreplanen for matematikk I England, for hvert område av matematikk skissert, er det både en lovfestet element og en ikke-lovfestet element. Det lovbestemte elementet er som følger:
- Multipliser og del tall mentalt basert på kjente fakta
- Del tall opp til 4 sifre med et ensifret tall ved hjelp av den formelle skriftlige metoden for kort divisjon og tolk remainders hensiktsmessig for konteksten
- Multipliser og del hele tall og de som involverer desimaler med 10, 100 og 1000
- Løs problemer som involverer multiplikasjon og divisjon, inkludert bruk av deres kunnskap om faktorer og faktorer. multipler, kvadrater og kuber
- Løse problemer som involverer addisjon, subtraksjon, multiplikasjon og divisjon og en kombinasjon av disse, inkludert å forstå betydningen av likhetstegnet
- Løser problemer som involverer multiplikasjon og divisjon, inkludert skalering ved enkle brøker og problemer som involverer enkle priser.
ikke-lovbestemte notater og veiledning:
- Elevene tolker ikke-heltall svar på divisjon ved å uttrykke resultater på forskjellige måter i henhold til konteksten, inkludert med remainders, som fraksjoner, som desimaler eller ved avrunding (for eksempel 98 ÷ 4 = = 24 r 2 = 24 = 24,5 ≈ 25).
- Elever bruker multiplikasjon og divisjon som inverser for å støtte innføringen av ratio i år 6, for eksempel ved å multiplisere og dividere med krefter på 10 i skala tegninger eller ved å multiplisere og dividere med krefter på 1000 i konvertering mellom enheter som kilometer og meter.
Divisjonsaktiviteter År 5
Divisjon I År 5 utvikler seg gjennom bruk av remainders i svar. For denne leksjonen vil jeg se på en annen bruk manipulativ som lærere kan bruke til å lære 4-til-1-sifret divisjon.
hvis spørsmålet var 5 642 delt på 4, kunne vi representere dette ved å bruke et sted verdi diagram og sted verdi tellere som vi kan se nedenfor.
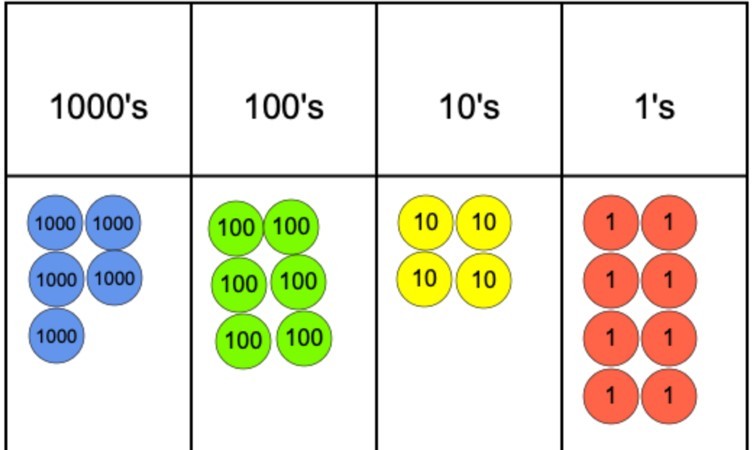
Det neste trinnet vil være å begynne å gruppere tellerne i 4 da dette er vår divisor. Men som det kan ses, kommer vi raskt til et problem i 1000-kolonnen, da vi kan gruppere 4 av tellerne, men da kan vi ikke gruppere gjenværende teller i en gruppe på 4.
for å bekjempe dette problemet kan 1000-telleren som ikke er gruppert byttes ut for ti 100-tellere. Disse kan da grupperes i grupper på 4, og dette kan skje uten at det er noen 100s tellere igjen. Derfra er det et enkelt tilfelle av å flytte til 10-tallet og til slutt de.
da det er ni 1s tellere, kan vi gruppere 8 av dem i 2 grupper og 4 og hevde at det er en igjen*. For å finne svaret, er alt som kreves å telle antall grupper som er gjort i hvert sted verdi og bruke disse til å skrive sifrene for å skape det endelige svaret. I dette tilfellet vil svaret være 1,412 resten 1.
* Når du ser på desimaler, kan du bytte de resterende 1s telleren for ti 0,1 tellere og fortsette divisjonen som beskrevet ovenfor. Studenter å være kjent med denne modellen er nyttig som det kan bidra til å avmystifisere divisjon med desimaler som elevene kan slite med. Dette hjelper dem å se at det er en videreføring av en prosess som de allerede er kjent med i stedet for noe nytt.
Divisjonsproblemer År 5
når de deles I År 5, vil studentene komme over scenarier der de må runde opp svaret for at svaret skal gi mening i sammenheng. Et passende spørsmål som demonstrerer dette ville være noe som følger:
en skole planlegger et sosialt distansert diskotek hvor de planlegger å tilby 250ml juice til hver elev. De kan kjøpe 2 liter flasker juice. De forventer 33 studenter å ankomme så vet at vil gi ut 8,25 liter juice. Hvor mange flasker juice trenger de å kjøpe?
et vanlig svar er at studentene vil si 4 og en fjerdedel. Men som du ikke kan kjøpe en fjerdedel av en flaske, i dette tilfellet er det riktige svaret ville være 5 flasker juice ville være nødvendig for å sikre at alle studenter kunne delta.
Divisjon: Resonnement Og Problemløsning År 5
som nevnt ovenfor, I År 5, vil studentene møte scenarier innenfor divisjon der de vil bli pålagt å velge om et svar må rundes opp eller ned. For eksempel, når et spørsmål ber elevene om å finne ut hvor mange busser som trengs for en skole en tur.
Å Få elevene til å lage sine egne problemer ved hjelp av en rekke gitt kontekst kan være en veldig utfordrende aktivitet som får elevene til å tenke matematisk om kontekst og divisjon.
Studenter kan deretter bytte disse spørsmålene de har opprettet med en partner og deretter gå om å løse dem og sjekke med den opprinnelige spørsmålet skaperen hvis de har det riktige svaret.
Divisjon År 6
I Den Nasjonale Læreplanen for matematikk I England, for hvert område av matematikk skissert, er det både en lovfestet element og en ikke-lovfestet element. Det lovbestemte elementet er som følger:
- del tall opp til 4 sifre med et tosifret heltall ved hjelp av den formelle skriftlige metoden for lang divisjon, og tolk remainders som hele tallrester, brøker, eller ved avrunding, etter behov for konteksten
- del tall opp til 4 sifre med et tosifret tall ved hjelp av den formelle skriftlige metoden for kort divisjon der det er hensiktsmessig, tolke remainders i henhold til konteksten
- utfør mentale beregninger, inkludert med blandede operasjoner og store tall
- identifiserer felles faktorer, felles multipler og primtall
- bruke sin kunnskap om rekkefølgen av operasjoner for å utføre beregninger som involverer de fire drift
Ikke-lovbestemte notater og veiledning:
- Løs problemer som involverer addisjon, subtraksjon, multiplikasjon og divisjon
- Bruk estimering til å sjekke svar på beregninger og bestemme, i sammenheng med et problem, en passende grad av nøyaktighet.
Divisjonsleksjonsideer År 6
Sophie Bartlett (@_MissieBee) har skapt en utmerket blogg her (link Til Sophies blogg om undervisning i lang divisjon) som beskriver hvordan hun ville lære lang divisjon for et år 6 klasse. Så lenge divisjon er den eneste nye læring på divisjon for År 6, dette er en ideell måte å innføre prosedyren for lang divisjon.
Divisjonsspørsmål År 6
et typisk divisjonsordproblem som En 6-årig student ville komme over, ville være:
en skole hevet £3,146 fra et bakesalg. 104 foreldre deltok på arrangementet. Hvis alle foreldre brukte like mye penger, hvor mye brukte hver foreldre?
her forventes studentene å bruke long division-metoden for å løse dette spørsmålet for å få svaret £30.25.
Divisjon: Resonnement Og Problemløsning År 6
med noe prosessuelt som lang divisjon, er en god resonnement aktivitet å få elevene til å finne feil. Disse ressursene gir en stor bank av slike aktiviteter. Som vi kan se fra spørsmålet nedenfor, har studentene gjort alt det harde arbeidet, men en uforsiktig feil i å telle gruppene på 59 betyr at barnet trodde 59 x 7 var 472 og ikke 59 x 8.
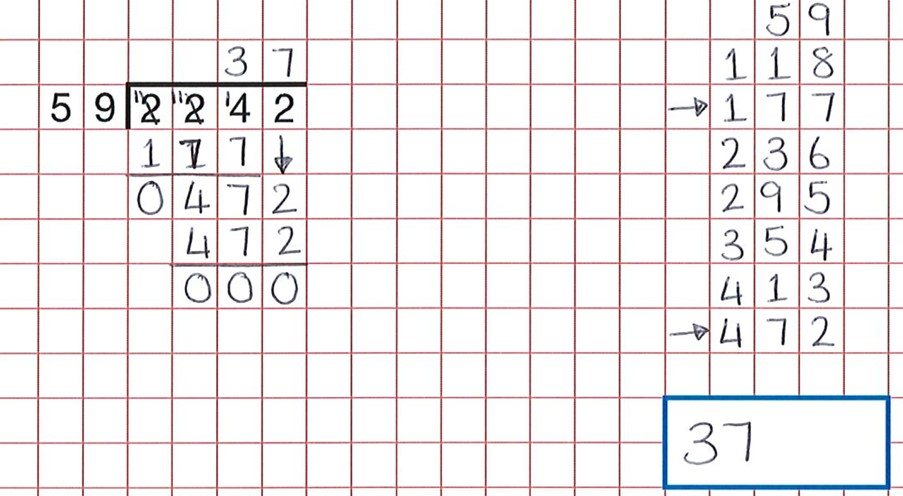
det riktige svaret ville vært 38.
Divisjon er et viktig matteemne, ikke bare PÅ KS2, men i matematikk som helhet. Forhåpentligvis dette innlegget har gitt deg noen gode ideer for å hjelpe elevene nærmer det med tillit.
online 1-til-1 matematikkleksjoner klarert av skoler og lærere
Hver uke third Space Learning maths specialist tutors støtter tusenvis av grunnskolebarn med ukentlige online 1-til-1 leksjoner og matematikkintervensjoner. Siden 2013 har vi hjulpet over 100 000 barn med å bli mer selvsikre og dyktige matematikere. Lær mer eller be om et personlig tilbud for å snakke med oss om dine behov og hvordan vi kan hjelpe.
Grunnskolen undervisning rettet mot behovene til hvert barn og tett følge Den Nasjonale Læreplanen.